多约束下的敏捷导弹大离轴转弯规律研究

韦亚利，殷 玮，刘印田，王 鑫，胡春朝

(上海机电工程研究所，上海 201109)

0 引 言

未来的空战要求导弹具有更强的机动能力、离轴发射能力和全方位攻击能力，尤其是对载机后方目标的攻击能力。为了应对后方目标，导弹在初制导阶段需完成时间短、半径小、转弯角度大的转弯。空空导弹的初制导转弯与垂直发射地空导弹的初制导转弯相似，但空空导弹的初始速度更高，转弯角度更大。能量损失与不同转弯速率密切相关，还需要考虑攻角对飞行速度的影响。大角度转弯过程中要经过大攻角非线性的阶段，在空间探测领域，有类似的卫星姿态大角度机动问题，方法是以三角函数为基础进行轨迹规划[1]。在大攻角条件下，导弹空气舵效会急剧下降，严重影响转弯速率的提升，因此需要寻求其他控制装置如推力矢量控制装置[2]或者反作用推力喷气装置[3]来提供导弹做大攻角机动的控制力和力矩[4-6]。文献[2]采用保持推力角180°的方式实现越肩发射初制导转弯，这种方式虽然能够实现速度拐弯的时间最优，但速度损失严重，并且没有考虑超大攻角下通道间的不稳定现象。文献[4]给出了直/气复合控制器参数选取方法，从控制器的角度提高了系统的快速性，但没有充分考虑指令形式的影响。文献[6]采用姿态控制的方法实现导弹越肩发射，但其姿态角指令无法保证拐弯期间维持大攻角，拐弯快速性仍待提升。

为此，针对目前一种尾部采用发动机引流提供姿控直接力的导弹方案，本文在转弯快速性约束、弹速约束、速度到位角约束、弹体姿态角约束等多个约束条件下，设计了初始大机动转弯规律，在直接力作用时间内完成导弹最大180°转弯，并保证各约束条件均满足设定要求。

1 模型描述及分析

1.1 直接力推力模型

直接力装置安装于发动机尾部，从主发动机燃烧室引流，总共有6个直接力喷管，其后视图如图1所示。左右各1个喷管(3#和6#)为大喷管，提供转弯需要的偏航力矩；上下各2个喷管(1#、2#、4#、5#)为小喷管，提供俯仰及滚转力矩，每个喷管都可以独立工作。燃气阀门可重复开启与关闭，但有开启次数限制。直接力响应时间(指令生成到直接力稳定输出时间)小于20 ms。直接力装置工作时，产生的力矩如式(1)所示。

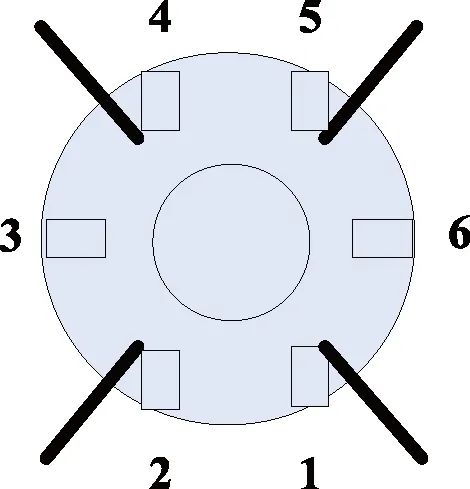
图1 直接力装置后视图Fig.1 Rear view of direct force device

(1)

式中：Mx1、My1、Mz1为作用于导弹上的直接力产生的力矩在弹体坐标系各轴上的分量；fx、fy、fz为作用在导弹上的直接力在弹体坐标系各轴上的分量；rc为直接力作用点与弹轴的距离；xc为直接力作用点距头部距离；xg为弹体质心距头部距离。

1.2 动力学模型

建立导弹在瞬时转弯平面内质心运动的动力学方程[6]，在不考虑重力影响的条件下为

(2)

(3)

式中：m为导弹实时质量；v为导弹实时速度；θ为导弹实时弹道倾角；α为导弹实时攻角；P为发动机推力；FX3、FY3为气动力在速度坐标系X、Y轴方向的投影。

2 转弯规律设计

初制导转弯到位包括姿态角到位和速度方向到位。设计姿态角指令遵循最佳轴控制原则，设计攻角指令通过最优控制理论。通过指令的动态分配，实现初制导转弯结束时刻的姿态角到位与速度方向到位，并且满足转弯过程中的导弹速度要求。转弯过程中执行机构为直接力装置，对应稳定控制系统回路结构见图2。图2中，Km、Ksf、Kz表示稳定控制系统控制器参数。

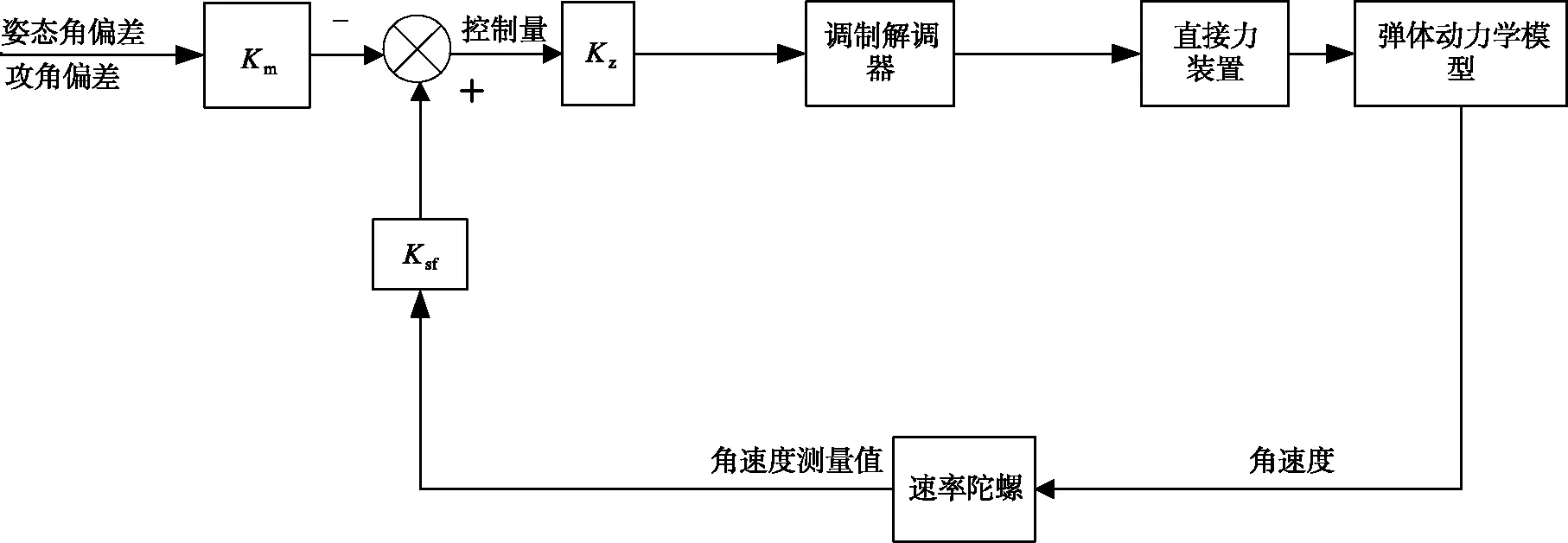
图2 初制导转弯段的稳定控制系统回路Fig.2 The loop of the stability control system at the turning phase of initial guidance

2.1 最佳轴控制原理下的姿态角指令

根据最佳轴控制原理，导弹纵轴可绕一最佳轴最快地转至指向矢量(即转弯结束时的导弹指向)上，导弹纵轴与指向矢量间的夹角即等待消除的控制误差信号。

ϑmax=cos-1(Tg11Az11+Tg21AZ21+Tg31Az31)

(4)

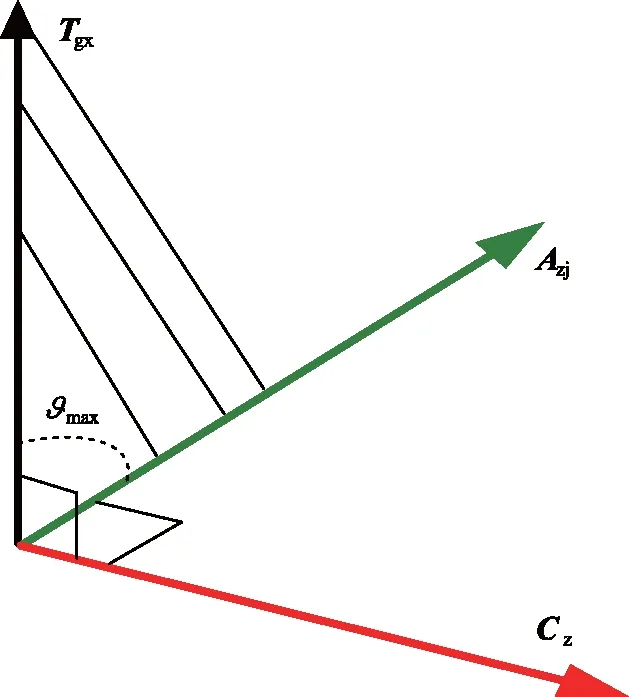
图3 最佳轴示意图Fig.3 Schematic diagram of the optimal axis

按照转弯时间，得到转弯过程中任意时刻需要消除的控制误差信号见式(5)。

(5)

式中：dT1+dT2=dT=Tend-Tbegin，为初制导转弯阶段持续时间。

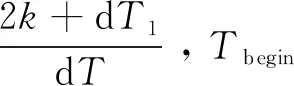
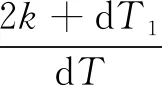
2.2 最优控制理论下的攻角指令

选取导弹实时速度v、导弹实时弹道倾角θ为状态量，根据式(2)、式(3)得到如式(6)所示状态方程。

(6)

边界条件为

(7)

最快转弯速率要求在最短的时间内完成弹道角变化，用泛函指标描述为

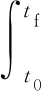
(8)

攻角α作为控制变量，即u=α。

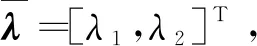
(9)

(10)

协态方程为

(11)

同时，由横截条件可以确定协态向量的终值为

λ1(tf)=0,λ2(tf)=0

(12)

这样就构成了最快转弯速率的两点边界问题。很难获得式(11)解析解，因此对其中的气动分量进行简化。

由式(11)可得

(13)

由式(10)可得

sin(αc)=0

(14)

可知，在αc=180°时可最快地完成速度转弯。

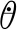
由式(2)可以看出，攻角越大，主发动机推力在速度方向上的分力越小，且气动阻力越大，从而引起导弹减速。由于敏捷导弹对转弯结束时刻的弹速有要求，因此在弹速接近最低速度时，应对攻角指令限幅，避免导弹继续减速。在导弹气动布局和外形尺寸给定的情况下，在高度变化范围不大的条件下，气动阻力随着导弹速度的增大而增大，在弹速为最低速度时需满足式(15)。

(15)

对于可用攻角范围α∈(0,90°)，由于气动阻力符号为负，且随着导弹攻角的增大而增大[8]，推力分量Pcosα随着导弹攻角的增大而减小，因此αmax存在唯一解满足式(16)。

Pcosαmax+FX3|v=vmin=0

(16)

由于气动插值对攻角的限制最大为70°，最快转弯速率原则下带末速限制的攻角指令为

(17)

2.3 指令动态分配

在纵向平面内姿态俯仰角ϑ与攻角α存在一定的关系，如式(18)所示。

ϑ=θ+α

(18)

由于姿态响应比速度响应快，而攻角的响应是通过姿态角变化来实现的，为了保证转弯速率，并且保证转弯结束时的姿态到位，需要按照一定的分配原则来实现姿态角指令与攻角指令的响应，如式(19)所示。

(19)

式中：tswitch为速度到位时刻。

3 制导控制系统建模与仿真

以某型导弹为例，建立初制导转弯段制导控制系统模型，图4为导弹初制导转弯段制导控制系统原理图。

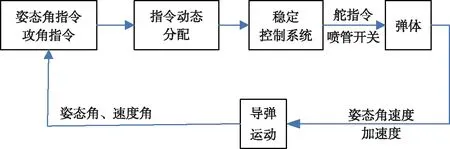
图4 导弹初制导转弯段制导控制系统原理图Fig.4 Schematic diagram of the guidance control system at the turning phase of initial guidance

仿真条件如下：

初始速度390 m/s，初始攻角0°，初始俯仰角0°，初始偏航角0°，初始滚转角0°；

直接力：3#、6#喷口推力1 400 N，1#、2#、4#、5#喷口推力700 N，作用时间4 s；

转弯过程中速度要求：不小于270 m/s。

初制导段仿真结果如图5所示。

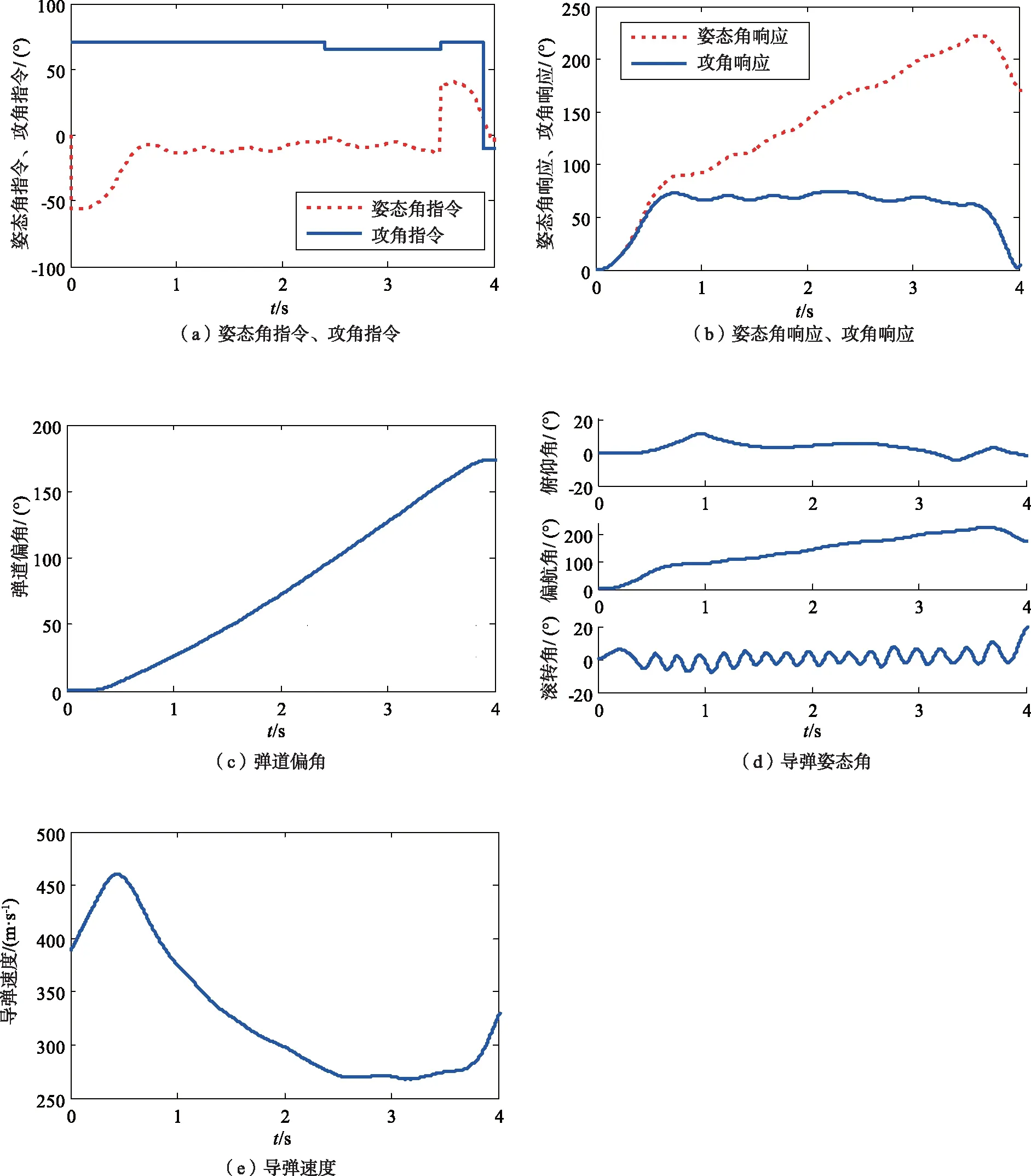
图5 仿真曲线图Fig. 5 Simulation curves

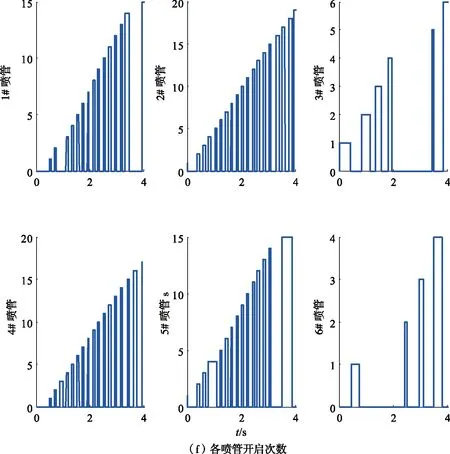
图5 (续)

由仿真结果可以看出，转弯开始后为了保证转弯速度，攻角快速达到最大可用值并维持，直到2.5 s弹速不满足转弯过程最低速度要求，攻角指令变小，从而保证了弹速。在速度转弯到位后，姿态角指令实现了姿态到位。4.0 s转弯结束时，弹道偏角为175°，偏航角为172°，攻角为2°，弹速为327 m/s。实现大离轴转弯的同时，创造了较好的初中/末制导交班条件。全弹道仿真显示，面对尾追的目标时，载机可以采用后向攻击方式，实现对后方近距5 km目标的打击，见图6。

图6 全弹道弹目运动示意图Fig. 6 Full trajectory of target-missile movement

4 结束语

本文针对敏捷导弹大离轴转弯设计了一种多约束条件下的转弯规律。该方法受最佳轴姿态角转弯与最快速率转弯的限制，同时又保证了敏捷导弹转弯过程中的最低速度要求。通过先保证速度到位、后保证姿态到位的策略，实现了大离轴转弯。