10kV交联聚乙烯电缆中超声波传播规律∗

倪 辉 吴旭涛 余海博 程养春 何宁辉 马波 马云龙 李日东 郑夏晖 邢 琳

(1 国网宁夏电力有限公司电力科学研究院 银川 750002)

(2 华北电力大学 新能源电力系统国家重点实验室 北京 102206)

(3 国网河北省电力有限公司经济技术研究院 石家庄 050000)

0 引言

交联聚乙烯(XLPE)电力电缆被广泛应用于各大城市供电网络中[1]。电力电缆故障往往能够引发重大的电网安全事故，造成巨大的经济损失[2]。局部放电(局放)缺陷是引发电缆故障的重要诱因，及时发现电缆中的局放缺陷非常重要。电力电缆局放缺陷检测技术包括电检测法和非电检测法两大类。电检测法有脉冲电流法、电磁耦合法、差分法、特高频法等，非电检测法有超声波法、温度法、光检测法，以及用于附件检测的红外成像法和紫外成像法等[3−14]。

超声波法通过检测局放引发的超声信号来检测局放缺陷，并诊断缺陷所在位置。通常认为，局放发生时，一方面放电区域介质受到带电粒子的剧烈撞击，另一方面介质由于放电发热而瞬间体积膨胀，从而产生介质疏密波，这也就是声波[3,15]。超声检测法可以避免与电缆直接电气连接，适用于电缆局放在线检测，并有效降低外界电磁环境对检测的干扰；与光纤传感技术相配合，可以实现分布式、准分布式检测，因而近年来受到广泛关注。

Wang 等[16]在XLPE电缆中间接头制作了内部气隙、毛刺、滑闪、悬浮放电4种缺陷，并利用压电陶瓷超声波传感器获取了这4种缺陷的局放超声波信号波形，探讨了波形的时域和频域特征。李继胜等[17]在实验室环境下获得了XLPE 材料上的尖端放电气隙放电和沿面放电3种缺陷局部放超声信号的时域特征和相位谱图特征，研究了不同电压与最大放电幅值平均放电幅值及放电次数之间的关系。Rohwetter 等[18]利用单模光纤Sagnac 超声传感器研究了电缆接头的硅橡胶在交直流电压下的局放过程，在正极性直流局部放电起始电压(Partial discharge inception voltage,PDIV)以上同时测到了大约100 pC的直流局放脉冲，验证了Sagnac 光纤传感系统在电缆接头典型缺陷局放检测上的性能；Rohwetter等[19]还利用基于瑞利反射相干光时域干涉的准分布式光纤超声检测系统检测40 kV XLPE电缆接头的局放缺陷，测到了nC级的放电信号，首次证明了这一准分布式光纤声传感技术是电力电缆接头和端子局放超声监测的一种候选技术。Czaszejko等[20]利用布拉格光纤光栅传感器检测XLPE 试品内部和沿面的局放超声信号，能够检测到10 pC的内部放电。

放电量的大小、放电源的位置和放电缺陷的种类对于局放缺陷的诊断至关重要。电气设备的绝缘通常由多种复合绝缘材料组成，结构复杂，许多绝缘材料对声波的衰减和声速的影响都不同，会对局放强度测量和放电源定位造成影响[3]。因此，研究局放超声信号在XLPE电缆中的传播衰减规律至关重要，只有掌握该规律之后，才能依据传感器所在位置的超声信号推断放电源的位置及放电强度。李科林[21]通过仿真研究了局放超声波在XPLE电缆附件中的传播特性，指出在电缆终端法兰、接头金属压缩管外围的铜槽和临近接头电缆外接金属卡具等部位外置安装超声波传感器能够获得较高的灵敏度。在高模量固体介质中，声波传播距离较远，而低模量固体中声衰减大，声传播距离较近。

局放产生的超声信号一般来说比较小。此外，XPLE电缆由多层复合绝缘材料组成，超声传播过程复杂、衰减比较严重，这必然对现有超声检测传感器的灵敏度提出挑战。现有关于XPLE电缆中超声信号传播规律的研究很不完善，缺乏在实际电缆上的实测数据，缺乏明确的衰减规律，难以通过传感器所在位置的超声信号推算局放强度。

为了研究超声波在电缆中的传播规律，建立了10kVXLPE电缆本体的声压场仿真模型，详细研究了超声波从声源点开始在电缆中的传播过程；通过搭建10kVXLPE电缆超声衰减实验系统，实测了10kVXLPE电缆本体中超声波衰减情况。

1 电缆中超声波的衰减问题

图1是所研究的某型号10kVXLPE电缆的本体结构示意图，由铜导线和多层介质组成，各层材料的相关参数如表1所示[21]。当绝缘中存在气泡、杂质颗粒或者绝缘内外表面有半导电层突起的尖刺时，局放易从这些绝缘的薄弱处发生，随之而生的超声波信号也会从这些位置开始向电缆的各处传播。

在无限大均匀介质中，波的传播模态比较单一，只有横波和纵波这两种波。但当波与边界相互作用时，就会产生新的类型的波。这类波一部分被视作入射波的反射波，另一部分是与边界相关的完全新的类型的波(如瑞利波或表面波等)，具有多模态特性和频散特性，波的传播就变得复杂。目前只有关于一些简单的有界结构(如杆、梁、薄板、薄膜等)中波传播的比较成熟的结论，对于具有复杂边界结构的电力电缆中波的传播的研究还不成熟，所以局放超声在电缆中的传播过程不清楚，对其衰减的研究仅限于幅值大小变化的研究，缺乏幅值衰减和传播过程之间影响机制的研究，也就不能完全掌握幅值衰减所包含的所有信息，研究结果难以对工程实际有指导意义。

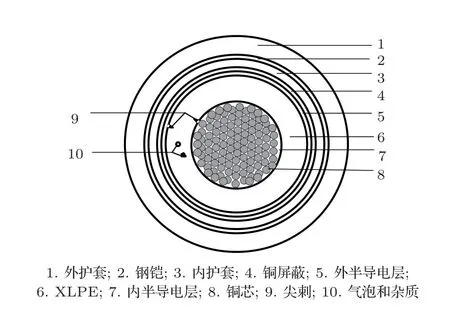
图1 某型号10kVXLPE电缆截面和绝缘缺陷示意图Fig.1 Map of a 10kVXLPE cable section and defection

表1 10kVXLPE电缆各层媒质声学参数Table1 Acoustic parameters of each layer structure of 10kVXLPE cable

2 电缆中超声波幅值衰减规律仿真分析

2.1 仿真模型

利用COMSOL有限元仿真软件按照表1所示的10kVXLPE电缆本体结构参数构建三维仿真模型并模拟局放脉冲声源声压场，仿真计算超声波传播过程。用高斯脉冲波形体积流率模拟电缆局放频带声源，表达式如下：

其中，Qs是体积流率，单位m3/s；A是体积流率初值，A=1 m3/s；脉冲峰值时间tp=10 µs；f0=50 kHz，其波形及频谱图如图2所示(后文实验中声源波形和仿真一致)。

根据声学知识可知，在某一媒质中插入某一厚度的中间层时，声波从中间层的一侧透射到另一侧时的反射波和透射波的大小，不仅与两种媒质的特性阻抗有关，还与中间层的厚度有关。当中间层的厚度和声波波长相比很小时，声波可以完全透过，中间层可以忽略。钢铠和铜屏蔽均只有0.2 mm，本仿真中设置的声源3 dB频带是2.72 kHz∼40.82 kHz(见图2(b))，按照电缆材料最小声速1900 m/s计算(见表1)，电缆中的声波波长均大于46.55 mm，是钢铠和铜屏蔽厚度的至少233倍，故可以近似认为钢铠和铜屏蔽可以被声波完全透过。基于以上理论，为了简化仿真模型，提高计算效率，在建立模型时忽略了钢铠层和铜屏蔽层，但同时为了保持电缆外尺寸不变，这两层均用临近的护套材料代替，仿真模型轴向切面示意图如图3所示。模型轴向长度设为1 m，径向尺寸与真实电缆一致。在模型上建立三维直角坐标系，如图3所示切面在z=0 平面上，为模拟XLPE中的内半导电层尖刺缺陷，将声源设置在模型左端内半导电层和铜芯之间点S处，S的坐标是(0,12.4,0)。

图2 高斯脉冲声源波形及频谱Fig.2 Waveform of Gauss pulse sound source and its spectrum

图3 电缆本体声压场仿真模型Fig.3 Model of cable sound pressure field simulation

2.2 仿真结果分析

局放超声传感器一般安装在电缆外护套表面，按照图3坐标系，在模型z=0 平面上的外护套表面沿轴向的不同距离处设置声压检测点Ti(i=1,2,···,19)，其y坐标yi=0，x坐标如表2所示。

检测点T1、T6和T10的声压时间曲线p-t如图4所示。可见，曲线随时间均呈振荡衰减趋势，并且随检测点距声源距离增加而逐渐呈现出峰值能量分散的现象，这一现象和声波在与多层介质边界作用时发生折/反射有关。接下来主要分析检测点声压峰峰值的变化规律，实质上反映的是p-t曲线中的最大峰值的变化规律。

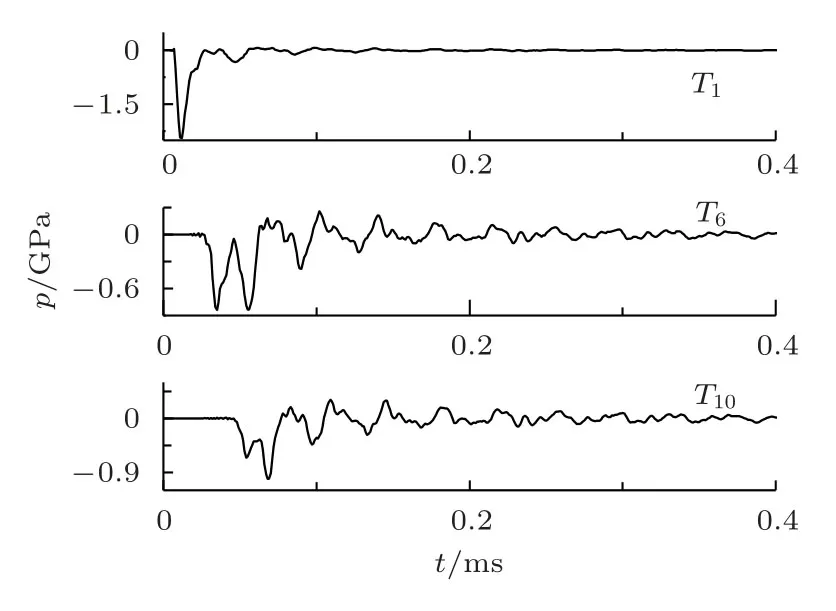
图4 检测点T1、T6、T10 声压时域波形仿真结果Fig.4 Sound pressure-time curve of detection points T1,T6,T10

表2 声压检测点x坐标Table2 x coordinate of detection points of acoustic pressure

检测点声压峰峰值和距声源点轴向距离(传播距离)的关系pp-p-x如图5所示，按照曲线变化趋势可以将其分为4个区间：A：x ∈(10,30)；B：x ∈(30,60)；C：x ∈(60,100)；D：x ∈(100,1000)。本文对这4段数据分别选择最优的模型进行拟合，拟合结果如图6所示。区间A声压峰峰值和距声源点轴向距离符合反幂函数关系，区间B符合二次函数关系，区间C符合一次函数关系，区间D符合“指数+常数项”的函数关系。

电缆内部声波从声源点开始会经历一个扩散的过程，扩散过程的发展可以反映在波阵面的变化上。如图7和图8所示，电缆内部超声波波阵面的形状逐渐由不规则的曲面向平面过渡，在距声源点大约113 mm的位置，波阵面已经基本变成平面，这说明在电缆内部声波的扩散过程在大概113 mm处结束，大概对应于图5、图6曲线100 mm处。电缆内部声波扩散的过程示意图如图9所示，声波从声源点开始向四周扩散，可以推断当波阵面完全抵达电缆的边界时，区间A的扩散过程结束，可以根据公式(2)计算得到此时声波传播的距离L1约为26.44 mm，和区间A拟合曲线的终止位置30 mm 基本一致，证明了仿真及分析的正确性。同时，区间A的曲线拟合结果显示，电缆外护套表面声压峰峰值和距声源点轴向距离的0.65次方呈反幂关系，这意味着在区间A声波的扩散速度介于球面波和柱面波之间。区间B、C，声波波阵面仍然在向平面的过渡阶段，扩散过程还在继续。从时间上来估计，区间B和区间C出现的声压峰峰值的变化趋势可能分别是“铜芯面”以及“下电缆表面”的反射波到达了“上电缆表面”的缘故。区间D，波阵面基本成为平面，电缆表面声波峰峰值减小的主要原因是声波透射到了电缆外部，但其透射系数很小，其声波峰峰值随传播距离减小的平均速度为3.61×10−4GPa/mm，远小于区间A的2.82×10−2GPa/mm。

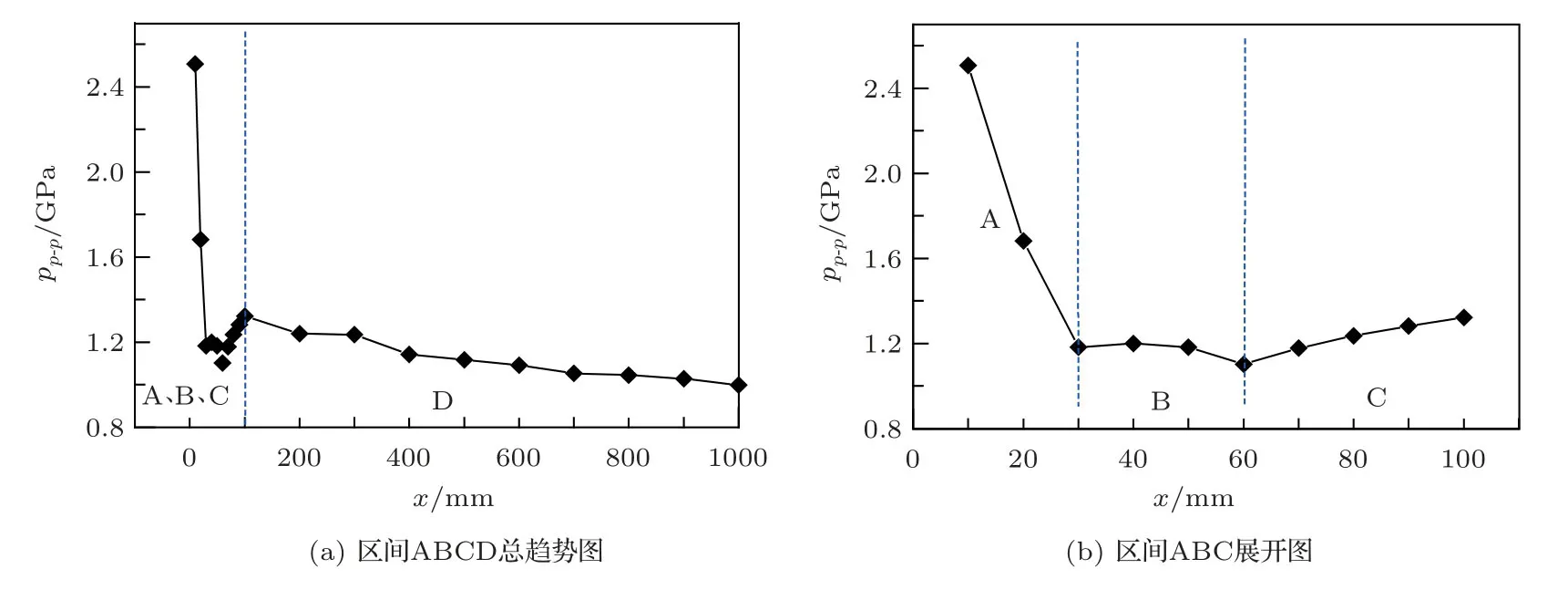
图5 pp-p-x曲线Fig.5 Curve of pp-p-x

图6 仿真中电缆表面声压峰峰值分段拟合曲线Fig.6 Piecewise fitting curve of sound pressure amplitude on cable surface in simulation

图7 不同时刻电缆z =0 切面声压场分布Fig.7 Distribution of sound field in cable section of z =0

图8 电缆横切面声压场分布Fig.8 Distribution of sound pressure field in the cross-section of cable

图9 电缆中超声波扩散过程示意图Fig.9 Schematic diagram of diffusion process of ultrasonic in cable

综上可知，电缆内部超声波的扩散过程受到电缆结构影响而只能进行一段距离，对于仿真中型号的电缆，局放超声波在电缆内部有限的扩散过程大约在距声源100 mm处结束。在有限的扩散距离上，电缆表面声波峰峰值的衰减很快，衰减速度明显比扩散结束后快。

3 电缆中超声波幅值衰减实验及分析

3.1 实验系统

本文搭建了长度为3 m的某型号10kV单相电缆超声波衰减规律试验平台，实验系统如图10所示。用信号发生器产生和图2波形形状一致且幅值为10 V的脉冲电信号来激励压电传感器(Piezoelectric transducer,PZT)产生声波信号作为声源，同时用另一个PZT 对电缆外护套表面的声波幅值进行检测。

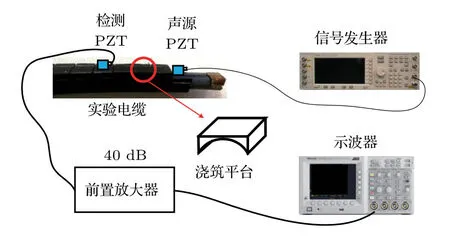
图10 实验系统图Fig.10 Experimental system diagram

电缆的端部绝缘层以外被剥除，绝缘层被打磨成厚度为1 mm的平台，声源PZT放置在该平台上，能够通过紧密接触的平面将超声波注入电缆。检测PZT被逐次布置在和声源PZT夹角为零的电缆外护套表面距声源PZT分别20 mm、30 mm、40 mm、50 mm、60 mm、70 mm、80 mm、90 mm、100 mm、200 mm、300 mm、400 mm、500 mm的位置。为了增大PZT检测的灵敏度，在电缆外护套的检测点用环氧树脂浇注成一个个PZT安装平台，同时给声源PZT和检测PZT 均施加11 N的力，以增强耦合效果。检测结果表明，和没有增敏措施相比，检测幅值增大了1倍左右。

3.2 实验结果分析

电缆外护套声波检测数据经滤波后如图11所示，和仿真一样，曲线随时间均呈振荡衰减趋势，并且随检测点距声源距离增加而逐渐呈现出峰值能量分散的现象。每个检测点测得3组数据，滤除噪声后求得峰峰值的平均值Up-p，将Up-p和传播距离x进行曲线拟合，最佳拟合公式如式(3)所示，拟合曲线如图12所示，可决系数R2=0.96，可见，实际电缆中超声波幅值随传播距离的衰减是符合指数规律的，此规律可以用于电缆局放位置或局放强度的估算。其衰减系数.α=0.07 Np/mm(或0.62 dB/mm)，U0=1678.63 mV，已知超声波在硅橡胶材料中衰减系数为0.40 dB/mm[22]，实际电缆结构中超声波衰减系数是其1.55倍，所以实际电缆结构中超声波的衰减相对来说是比较严重的，其原因和电缆本身结构复杂有关，比如电缆的钢铠层和外护套及内护套之间实际上有很多气隙，会加剧超声波的衰减，这无疑增加了电缆局放超声波检测的难度，对传感器的灵敏度提出了更高的要求。

图11 检测点声波实测结果Fig.11 Acoustic wave on detection points

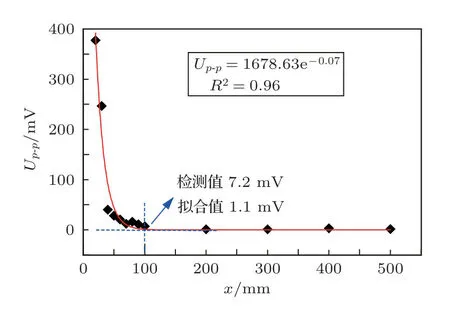
图12 实验声波幅值衰减指拟合曲线Fig.12 Experimental acoustic amplitude attenuation refers to the fitting curve

并且，从图12显然可以发现，在约100 mm处是一个转折点，从声源至100 mm之间超声波峰-峰值衰减速度最快，此规律和仿真一致，从而也证明了前文超声波在电缆中扩散过程理论的正确性。因此，针对实验中规格的电缆局放超声检测，传感器布置在距局放易发位置100 mm以内比较合理。

如图9所示，若将L3=100 mm处确定为扩散过程结束位置，此时波阵面平面化程度用扩散半径r和电缆直径2R0之比k表示：

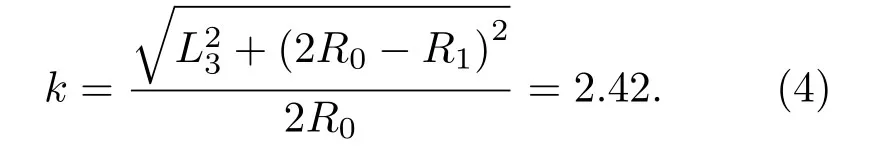
k值越大，波阵面相对越接近平面。本文中电缆k值大于2.42 就可以判定波阵面已经近似平面，扩散过程基本结束。因此可以按照公式(4)的原理来估计任意型号电缆中声波扩散过程结束的位置。

4 讨论

将图7所示声压图的颜色图例范围调小至107Pa得到如图13所示的声压分布图。对比图7和图13可发现，电缆中的声波可以分为两个分量：一个分量声波幅值较大(主要分量)，如图7所示，约在109Pa的数量级，其在整个电缆结构中的传播速度基本一致；另一个分量声波幅值较小(次要分量)，如图13所示，约在107Pa的数量级，其在铜芯中的传播速度大于外层绝缘。原因可能是局放超声在电缆中的实际传播路线与x轴有夹角，会不断在铜芯与外层绝缘的界面来回反射，从而沿“Z”字形路线轴向传播，这样传播路径会变长，可造成声波在铜芯中传播速度和外层绝缘一致的现象。相反，铜芯中与x轴平行的声波的传播速度自然大于外层绝缘。

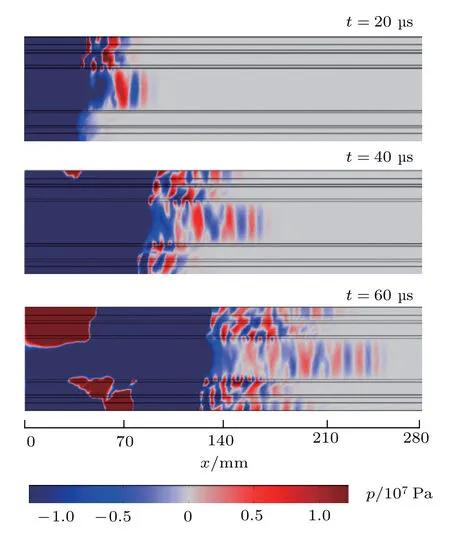
图13 缩小图例范围的不同时刻电缆z =0 切面声压场分布Fig.13 Distribution of sound field in cable section of z =0 when the scope of the legend is reduced

局放声源是一个点声源，其初始波阵面是一个球面，声波传播方向中和电缆x轴平行的声束自然少于非平行声束，所以沿“Z”字形路径传播的声波能量比较大，声压也比较大，声压约是平行于x轴传播声束声压的100倍。

本文的结论是基于主要分量所体现的规律，也是电缆中声波幅值所体现的主要规律。关于主要分量和次要分量所蕴含的波的传播模态的解析研究或数值分析研究有待进一步展开。

5 结论

本文通过建立10kVXLPE电缆仿真模型，研究了模拟局放超声波电缆内部传播过程，并通过搭建10kVXLPE电缆超声衰减实验系统，实测了10kV单相XLPE电缆本体中超声波衰减情况，仿真和实验对比研究表明：

(1)实际10kVXLPE电缆中超声波幅值随传播距离的衰减是符合指数规律的，此规律可以用于电缆局放位置或局放强度的估算。声波衰减系数α=0.07 Np/mm(或0.62 dB/mm)，是硅橡胶材料中的1.55倍，故衰减比较严重，增加了电缆局放超声波检测的难度，对传感器的灵敏度提出了更高的要求。

(2)电缆内部超声波的扩散过程受到电缆结构影响而只能进行一小段距离，对于文中的10kVXLPE电缆，超声波在电缆内部有限距离的扩散过程大约在距声源100 mm处结束，扩散过程导致电缆表面声波峰峰值衰减严重，是电缆表面声波峰峰值衰减的重要原因。因此，考虑声波在电缆内部的扩散过程，建议此规格电缆局放超声传感器布置在距局放易发位置100 mm以内。

(2)用扩散半径r和电缆直径2R0之比k表示电缆内部波阵面平面化程度，当k值等于2.42时判定电缆中声波波阵面近似变成平面，扩散过程基本结束。此判断方法也可以推广到其他类似规格的电缆。