NOUS控制和PID控制的直流降压变压器控制性能对比

吴小康,SCHMID Robert，张 帆，张莹冰，赵晋泉

(1.河海大学能源与电气学院，江苏 南京 210098； 2.墨尔本大学工程学院，澳大利亚 墨尔本 3010)

直流降压变压器因载流量大、易于控制以及响应快等优点，广泛应用于机动车供电、机械手臂控制和通信系统能源供给等领域[1]。目前直流降压变压器产业面临的主要挑战包括高控制精度需求下对稳态响应无误差、对瞬态响应收敛速度快且无超调以及负载变化或环境干扰鲁棒性等[2]。直流降压变压器控制方法主要有比例积分微分(PID)控制和状态空间控制。

PID控制具有直接、程序简单等优点。周雪松等[3]为提高DC-DC变换器的抗扰性能，建立PID型滑模控制器，进而推导出系统等效控制表达式。张巍等[4]使用模糊PID控制无刷直流电动机，消除转矩脉动，削弱换相区转矩脉动，提升电机运行的鲁棒性。PID控制器设计的关键为对比例参数、积分参数和微分参数的选择，这些决定了控制的整体效果。PID算法中参数的选择和调整取决于设计者的经验和喜好，科学的设计方法包括对PID算法进行频域变换和分析[5]。

状态空间控制在拓展性方面具有优势，系统被抽象为一个矩阵后可以用数学的方法计算出控制向量对被控制系统的影响[5-6]。Glady 等[7]在POESLLC直流变压器上设计了一种补偿器和PID控制器进行对比，发现与PID控制器相比，补偿器可以提供更快的收敛速度。

笔者基于Schmid等[8-10]推导出的计算控制向量参数NOUS (non-overshooting and non-undershooting) 算法，设计了基于NOUS算法的状态空间控制系统(以下简称NOUS控制系统)，将该控制系统应用于直流降压变压器上，并设计PID控制系统与之进行对比，拟为寻找一种更加优越的直流降压变压器控制系统方案提供参考。

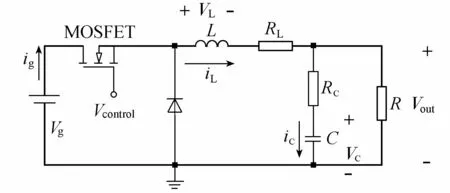
图1 直流降压变压器电路Fig.1 Circuit of DC-DC buck converter

1 直流降压变压器设计和建模

标准的直流降压变压器电路[11]见图1,图中Vg为电源输入电压，RC为电容内阻，C为电容，RL为电感内阻，L为电感，R为电阻，Vcontrol为方波控制电压。

分析图1中的电路模型，可得脉冲宽度调制(pulse width modulation， PWM)占空比d到输出电压Vout在频域s上的传递函数Gp[2，5]为

(1)

用现代控制理论分析电路可得状态空间模型(式(2)):

(2)

式中：Vload——负荷两端电压。

采用美国食品与药品管理局（FDA）有关口服固体药物利用度和生物等效性研究指南中推荐使用的 f2相似因子法［9‐10］来评价自研药（受试药品）与原研药（对照药品）体外溶出曲线的相似性，以考察其内在质量的差异。f2计算公式如下：

根据式(2)，定义A、B、C、D矩阵分别为

2 3种控制系统设计

2.1 NOUS控制系统和使用观测器的NOUS控制系统的设计

2.1.1NOUS算法

对于一个有p个极点的n阶系统，Moore设计了一种根据计算特征向量集V={v1,v2,...,vn},(vi∈Rn)和W={w1,w2,...,wn},(wi∈Rp)计算控制向量F=WV-1的计算方法[12]。构建Rosenbrock矩阵方程[13]：

(3)

式中：I——单位矩阵；λi——系统的特征值，每个特征值对应一个向量si，对于i=1,2,...,n-p,λi应等于系统的零点zi,对应的si为零矩阵。

Robert在此基础上提出了一种设计方法，在数学上证明了他的方法可以实现无超调控制，并命名其为NOUS控制：对于式(3)中i=n-p+1,…,n，λi可以随意选择，si=In-p+i。定义当前状态向量x(t)和稳态状态向量xss的差为ζ(t)=x(t)-xss，并定义变量α=[α1,α2,…,αn]T=V-1ζ(0)，根据选择的特征值λi计算α，当α满足判据时，闭环控制系统的瞬态响应无超调[8-10]。

2.1.2NOUS控制系统设计

将式(2)中A、B、C、D矩阵代入式(3)，根据选择的特征值(λ1,λ2)，可求得特征向量集V，据此算出α。对于二阶系统的NOUS算法，无超调的判据为(α1+α2)α2>0。如果选择的向量组不满足判据，则尝试下一组特征值。找到满足条件的特征值后可计算降压变压器的控制向量F, 并算出反馈向量参数[8]。NOUS算法程序的流程见图2。

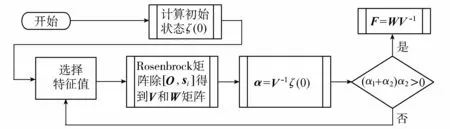
图2 NOUS算法程序的流程Fig.2 Flow chart of NOUS algorithm

在完成NOUS算法程序的基础上，用传感器测量电路中的参数变化，并据此更新NOUS算法控制器的参数，即可实现因负荷变化或扰动等原因系统参数发生变化时，该控制器的控制效果保持一致。

2.1.3 使用观测器的NOUS控制系统设计

观测器是在状态空间控制器基础上设计的附加控制系统。在实际应用中，系统的一些状态参数受环境条件或是成本限制等因素影响难以得到测量，使用观测器可以通过数学方法代替对部分参数的测量[5-6]。对于直流降压变压器，减去电流传感器可以为原型机减少约20%的成本。而实际产品中一般不需要配置开发板的单片机，因此不用电流传感器减少的成本会高于20%。通过添加观测器，可以减去这部分成本。

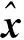
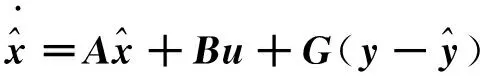
(4)

式中：G——观测器反馈增益；u——控制输入。

一般情况下，选择观测器的特征值使其收敛速度比闭环控制系统快2～6倍较为合适[6，14-15]。选定观测器特征值后可以计算得观测器反馈增益G。

2.2 PID控制系统设计

本文设计PID控制系统目的是作为NOUS控制系统的实验对照组在直流降压变压器原型机上运行。PID控制系统的设计目标为拥有尽可能短的瞬态响应时间，使瞬态响应无超调和具有鲁棒性[16-17]。本文用波特图进行PID控制系统参数选择。

标准PID控制的传递函数为[5]

(5)

式中：Kp、KI、KD——PID控制比例、积分、微分参数；K——传递函数的放大系数；Z1、Z2——传递函数的2个零点。

闭环传递函数正相关于式(1)(5)之积：

T(s)∝GP(s)GPID(s)

经过在波特图上绘制T(s)，选择Z1=0.1，Z2=10-6可以使150 Hz以上幅频降低以消除噪音；选择K=1.86，可以使阶跃响应无超调并获得最短的达到稳态时间。综上，PID控制系统的3个参数分别为KP= 0.186、KI= 1.86、KD=1.86×10-7。

3 3种直流降压变压器控制系统性能对比

分别从阶跃响应、鲁棒性对PID控制系统、NOUS控制系统和含观测器的NOUS控制系统的直流降压变压器控制性能进行对比。

3.1 阶跃响应测试

阶跃响应测试主要考察电路控制系统的稳态误差和瞬态响应的特性。根据应用的需要，会对瞬态响应的特性有各种要求，最常见的包括收敛速度快、无超调等。本文定义成功的降压变压器的阶跃响应具有的特征为：(a)10 V以阶跃响应内稳态误差小于0.1 V；(b)收敛到允许误差以内的时间短于20 ms；(c)瞬态响应无超调。0～6 V的阶跃响应实验中输出电压在示波器上的对比结果见图3、表1。

图3 3种控制系统下降压变压器0～6 V阶跃响应在示波器上的结果Fig.3 0-6 V step response of the buck converter with 3 controllers on oscilloscope

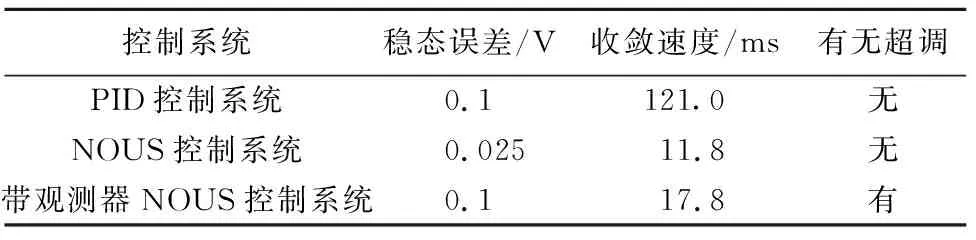
表1 3种控制系统下变压器0～6 V阶跃响应实验结果

图3中可看出：从稳态误差的角度考察，NOUS控制系统、带观测器的NOUS控制系统和PID控制系统都能实现稳态误差小于0.1 V；从收敛速度的角度考察，NOUS控制系统收敛速度最快，带观测器的NOUS控制系统其次，PID控制系统收敛速度较慢；从超调的角度考察，PID控制系统和NOUS控制系统都如设计预想一样，实现了瞬态响应无超调，带观测器的NOUS控制系统具有超调。

NOUS控制系统在阶跃响应中展现出优越性，它拥有更小的稳态误差，更快的收敛速度。而加入观测器的NOUS控制系统表现不佳，它的稳态误差较大并且阶跃响应有超调，和原本设计的意图不符，但在收敛速度上仍然优于PID控制系统。

状态空间控制需要非常精确的建模才能保证控制结果符合预期，在反馈信息充足的情况下，系统可以修正有限的误差，但是使用观测器的情况下，用计算代替一部分反馈向量的信息，导致误差被放大。而用相同的系统参数在MATLAB的仿真中NOUS控制系统和带观测器的NOUS控制系统的瞬态响应几乎完全一样，仅控制信号波形有些许不同，可见观测器会导致建模误差放大，使得控制效果与预期有差别。

3.2 鲁棒性测试

图4 负载电阻从21 Ω跳变为4.5 Ω时2种控制方法下变压器瞬态响应Fig.4 Transient response of the converter with 2 controllers when load changes from 21 Ω to 4.5 Ω

负载电路中加一个开关可以使负载电阻在4.5 Ω和21 Ω之间切换，本文将以此测试系统的鲁棒性。状态空间控制方法需要所有准确的系统参数进行建模，包括负载电阻，所以当切换负载电阻的时候，控制方法也需要进行实时更新。本文中NOUS控制系统的算法，包括根据NOUS判据寻找符合条件的极点程序都被翻译成C语言写入单片机使其能够检测负载电阻的变化并在线更新控制器算法。检测负载电阻需要对电流进行测量，而观测器的价值就在于代替电感电流测量，所以这里不加入鲁棒性测试对比。实验分别记录了NOUS控制系统和PID控制系统在电阻从21 Ω突变到4.5 Ω时的瞬态响应，结果如图4所示。

图4中，PID控制系统下直流降压变压器重新回到稳态的时间为8.1ms，NOUS控制系统下直流降压变压器重新回到稳态的时间为22.4 ms，证明了PID控制系统优越的鲁棒性。而状态空间控制下每次系统的变化都需要对控制程序进行重新计算，从检测到参数变化到计算出新的控制向量所花的时间以及这段时间内产生的较大输出偏差，导致其鲁棒性不如PID控制。

4 结 语

a. 基于状态空间控制的NOUS控制系统具有最优秀的瞬态响应和收敛速度。在设定值频繁变化，并且对控制的速度和精度有较高要求的时候，是更优越的控制方法。但是基于状态空间的算法需要对被控制系统进行准确的建模，这意味着系统中参数的变化会导致控制失效，不具备鲁棒性。因为状态空间控制的极点选择和控制效果均可量化，在NOUS算法中表现为满足一定判据下可保证瞬态响应的无超调，所以可以把控制程序的设计步骤写入单片机，让系统自行检查系统中参数的变化实时更新控制算法，实现鲁棒性。

b. 使用NOUS控制系统的直流降压变压器有成本较高的缺点，因为状态空间算法需要更多的反馈参数，在直流降压变压器中表现为额外的电流传感器的成本。但这个缺点可以通过设计观测器来弥补。带观测器的NOUS控制系统仍保留了收敛速度快的优点，但会导致控制系统建模中的误差被放大，影响输出结果。

c. PID控制系统在收敛速度和瞬态响应的波形均不如NOUS控制系统，但是具有程序简洁、鲁棒性好的优点。这两个优点使PID控制系统在现代工业控制中最为常用。

d. NOUS控制系统和PID控制系统各有优劣，在处理频繁的设定值变化时应选择NOUS控制系统；在系统无法精确建模，或系统模型需要持续变化时，PID控制系统是更好的选择。

NOUS控制算法在直流降压变压器控制上的应用仅仅是一种简单应用，它可以处理更高阶的复杂系统[9]。在复杂系统中，基于状态空间的控制算法更具价值和意义[18]。未来的研究可以着眼于更复杂的控制系统，如风电机控制、自动驾驶等，NOUS控制系统无超调的特性使其在这些领域会有更加具体和重要的意义。