塔式光热发电定日镜平面度参数测量的方法研究

胡 珂，龚 俊，程荣展

(兰州理工大学机电工程学院，甘肃 兰州 730050)

塔式太阳能光热发电是通过定日镜将太阳光反射的能量聚集驱动燃气轮机发电的技术。该技术按集热形式不同主要分为4类：槽式系统、塔式系统、菲涅尔式系统和碟式系统[1-2]。塔式系统的关键是太阳光聚集和热量储备，其中定日镜就是将太阳光反射到聚热塔上的集热装置[3-4]。塔式太阳能光热电站的定日镜场由上千块定日单元镜组成(以下称单元镜)，单元镜投资成本达到电站总成本的50%以上。按面积不同单元镜分为两类：一类是反射面积超过80 m2的大面积定日镜，如116.5 m2的Senner定日镜，95 m2的Lugo定日镜[5]；另一类是小于20 m2的小面积定日镜，如1.2 m2的Esolar定日镜[6]。为了解决由于太阳像差导致的反射光斑远距离散焦严重以及小面积定日镜反射辐射小等问题，人们将多块子镜拼接成小曲率抛物面形的大块组合镜。随着子镜拼接数量增加，子镜镜面角度发生偏转，拼接的精度无法保证，单元镜的平面度难以达到近似抛物面形的要求；加之电站所处环境自然条件恶劣，受风沙、雨雪等自然因素的影响，子镜和镜面支架易发生变形，同样使得子镜几何中心法线角度发生偏转。这些情况均使运行过程中的定日镜的平面度发生变化，经由单元镜反射的光线以漫反射的形式发散出去，导致太阳光斑无法精准反射到理想位置，因此大块定日镜平面度检测是塔式聚光型太阳能热发电的关键技术之一。因为子镜几何中心点位于抛物面上，所以塔式定日镜平面度测量的关键是子镜几何中心处的法线角度测量。

当前国内外提出的定日镜平面度检测方法多处于理论实验阶段：国外的Shortis等[7-8]在1996年提出摄影测量法，即利用相机对不同角度的镜面上的标志点拍照，通过共线原理确定被测面三维坐标，此方法检测精度较高，但标志点数量多，安装和标定费时费力，不适合快速和大面积检测。2006年，国外的Bothe与他的团队提出黑白条纹反射法，通过对比被测镜面调制后的图像和原黑白条纹图像，使用相移算法和图像处理得到曲面面形，但该方法更适合用于曲率更大的槽式镜面[9-10]。由此可知，塔式太阳能光热发电行业迫切需要一种新的定日镜平面度测量法。

1 平行光束聚焦法检测原理

1.1 单元镜误差源分析

单元镜将反射光斑投射到指定的吸热塔位置，需保证2个关键因素：一是子镜的面形精度；二是整块拼接单元镜的面形平面度。子镜的面形精度是决定反射光斑面积的关键，反射光斑在理想落点位置的重合度则取决于单元镜上每块子镜的拼接精度。

图1所示为子镜误差示意图，虚线模拟理想光线，实线模拟实际反射光线。子镜玻璃层厚Δd1，造成实际光线被反射时发生移位Δa1。由于镜面玻璃层厚度小，此误差属于毫米数量级，因此可以忽略不计。子镜在镜厂生产中，反射面不规则的突起会导致光线发生漫反射，产生移位Δa2，此误差亦属于毫米数量级，可以忽略不计。

图1 子镜误差示意图

图2 单元镜误差示意图

1.2 平行光束聚焦法测量原理及模型分析

平行光束聚焦及欧拉旋转定理法的测量原理是利用穿过凸透镜的平行光聚焦于其焦点上的性质，通过凸透镜焦点处垂直镜面布置的线激光在光屏上的投影，测得子镜的反射光线角度。

如图3所示，反射光线穿过凸透镜后聚焦于其焦点f上，D点是透镜焦点处的线光源在光屏上的落点，线光源的轨迹线重合于凸透镜光轴，A点为平行光束源，光束在镜面B点反射。由图中几何原理可知，根据像高和入射角呈比例的关系，测得落点D的位置后由正弦公式求得反射角β；再通过已知的A点和B点位置求得入射角α。最后由平行光束入射角和反射角根据欧拉旋转定律求得子镜的几何法线角度θ。

图3 平行光束聚焦法测量原理

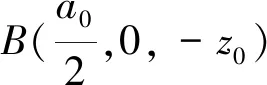
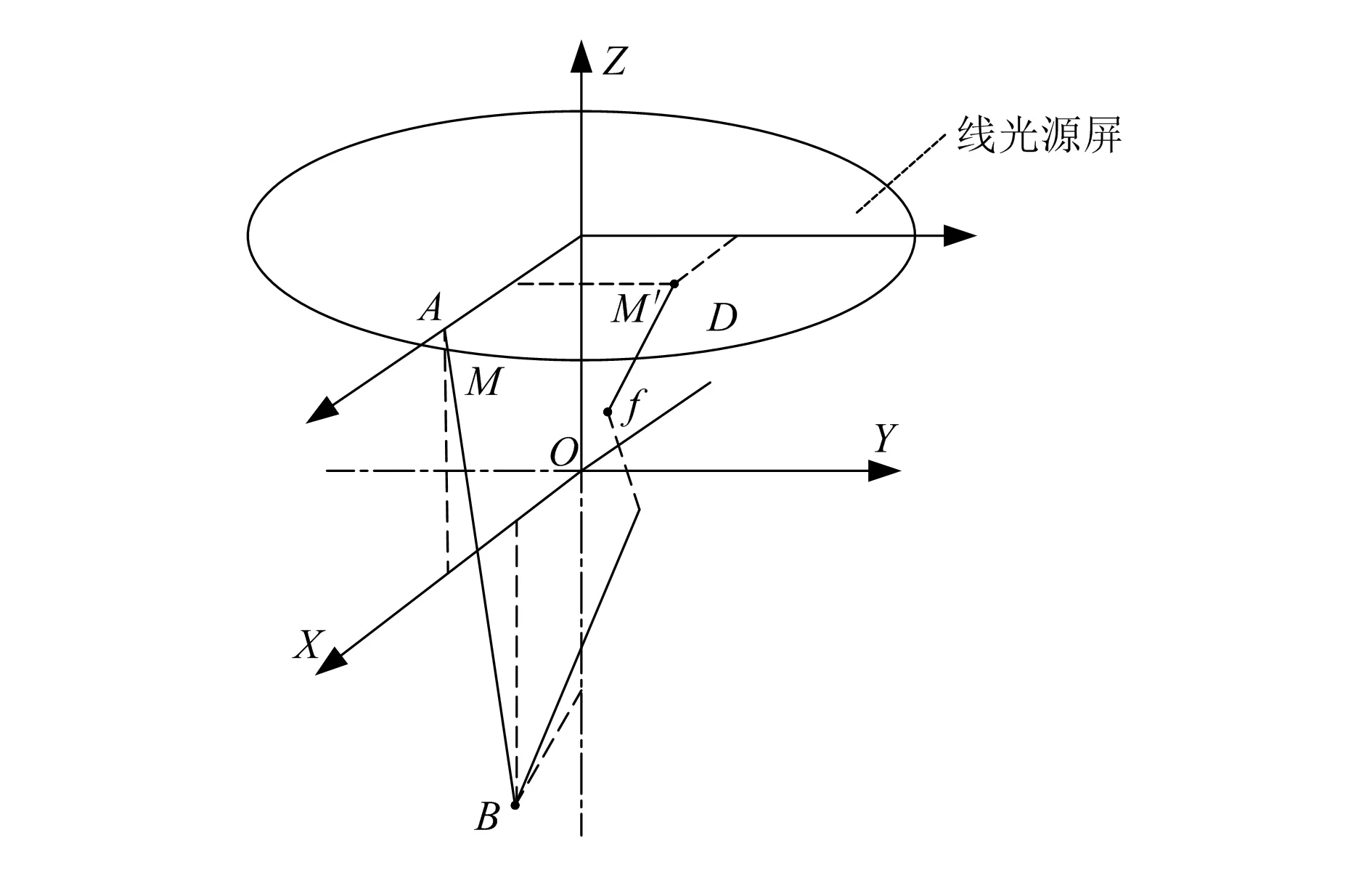
图4 平行光束聚焦法空间几何关系

入射光线AB的方向向量M的表达式为：

其中：

反射光线经过B点反射进入位于坐标中心处的凸透镜中发生折射，聚焦于f点，此时反射光线平行于线光源发射线OD，因此反射光线可由OD表示，且该方向向量M′为：

式中：x，y，z分别为旋转向量半径。

生成的旋转向量V为：

(1)

欧拉旋转角θ为：

(2)

欧拉旋转矩阵L为：

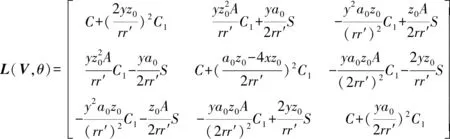
(3)

式中:C=cosθ;S=sinθ;C1=1-C;A=a0-4x。

在三维空间中，根据欧拉旋转理论，M′绕向量V旋转一定角度θ得到法线方向矢量L。

通过以上推导及式(4)：

H=L·M′

(4)

可得法线H的方向矢量，并通过角-轴关系表示为：

式中：αH为X轴与法线H的夹角；βH为Y轴与法线H的夹角；γH为Z轴与法线H的夹角。

2 子镜与单元镜的数学模型关系

2.1 单元镜的理想平面度参数模型

本文针对装配单元镜平面度测量提出的平行光束聚焦测量法与国外的哈特曼光学视屏扫描测试法[11-12]以及Sandi实验室提出的激光束扫描法不同，该方法旨在保证单元镜上子镜的拼接精度和随机检测镜场单元镜的运行状态，得到在任意时刻受多方面因素影响的结果，以及单元镜的平面度面形参数。定日镜运行过程中将太阳辐射反射至集热器有限区域内，同时还需克服因为太阳张角导致的太阳像差，即要保证太阳光斑不发生太大的散焦，因此超大面积拼接单元镜为平凹面或抛物面，国内多采用抛物面。图5所示为以单元镜空间几何中心为坐标原点建立的空间直角坐标系，以此分析子镜与单元镜之间关系的数学模型。

由图可知，各子镜的空间几何中心构成了该旋转抛物面，方程为x2+y2=4pz,其中点F(0,0,p)为抛物面的焦点，即p为单元镜几何中心到集热器之间的距离；点Bn(x,y,z)为抛物面上任意一点，且是平行光束在子镜的反射点。

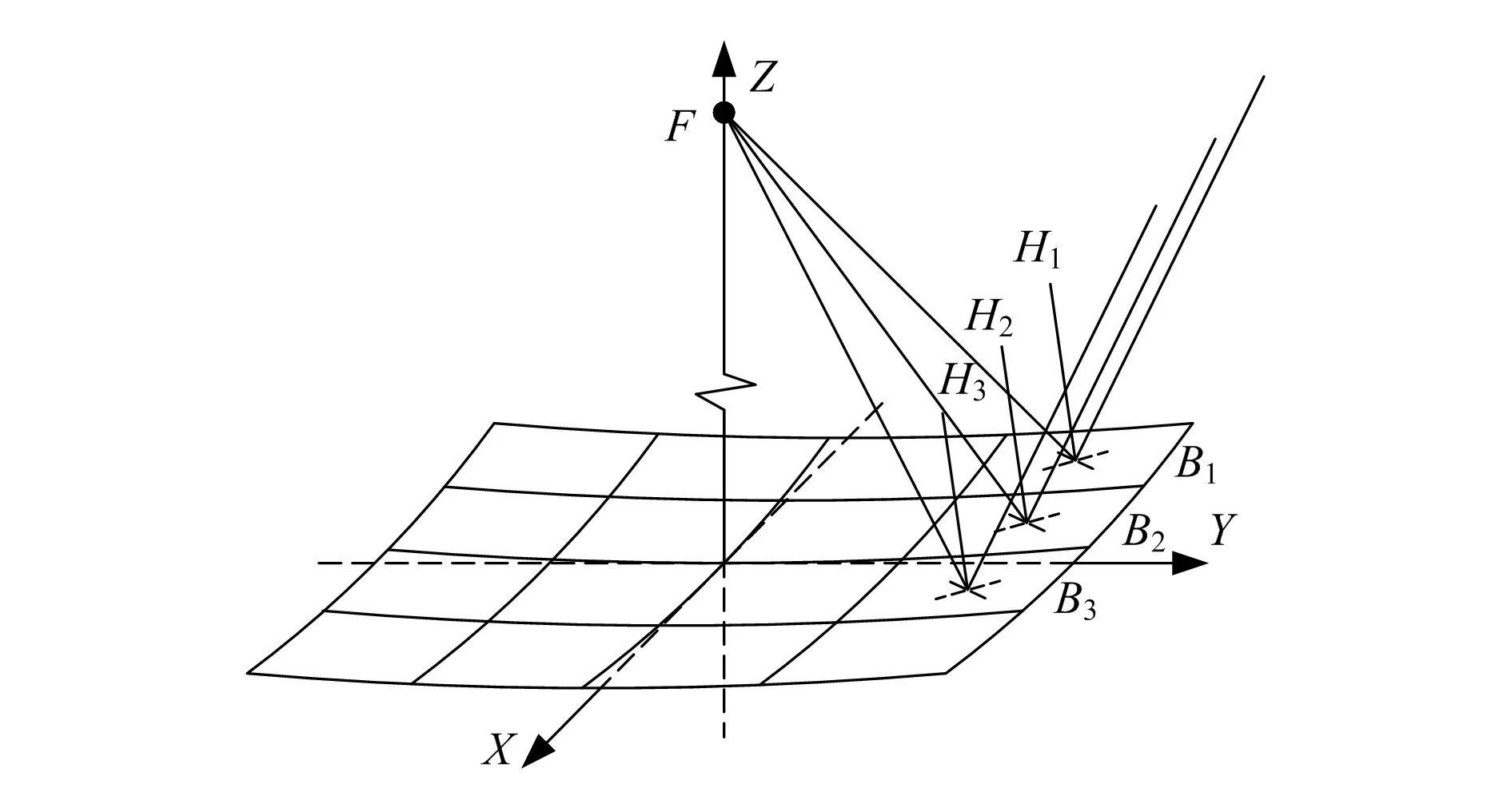
图5 子镜与单元镜的几何关系

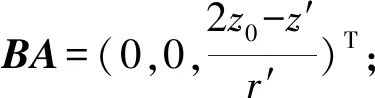
根据欧拉旋转定理，旋转向量：

(5)

BF绕向量V′旋转一定角度θ′即可得到法线方向矢量L′。

旋转角θ′为：

(6)

旋转矩阵L′为：

L′(V′,θ′)=

(7)

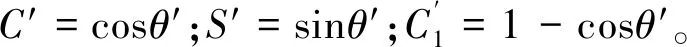
通过以上推导及式(8)：

H′=L′·BF

(8)

可得理想法线H′的方向矢量，通过角-轴关系可表示为：

(9)

式中：αH′为X轴与法线H′的夹角；βH′为Y轴与法线H′的夹角；γH′为Z轴与法线H′的夹角。

检测过程中，在求得理想状态下单元镜的平面度法线角度参数的前提下，将得到的实际子镜法线角度参数与其对比，即可直接通过线光源在光屏上的落点位置校正子镜角度，从而达到满足要求的单元镜平面度。

2.2 子镜偏转的角度误差允许范围

单元镜中的任一块子镜实际几何法线相对于理想几何法线偏转角度δ决定了反射光斑在聚热塔上的实际位置，如图6所示。

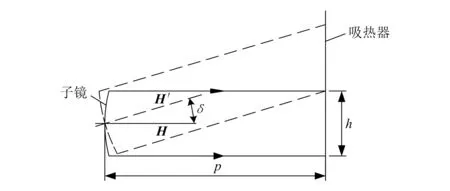
图6 子镜几何法线角度误差范围

图中实线代表理想反射光斑落点位置，虚线表示子镜倾转导致反射光斑在聚热点的实际位置，单元镜上任一块子镜偏转角度都局限于一定的范围，超出这个范围，光斑落点将不在理想位置，因为焦距远大于子镜边长，由图中几何关系可知实际法线和偏转法线的夹角即最大误差允许角δmax，近似表示为：

(10)

式中：hmin为子镜最小边长。

3 “大汉”定日镜检测实验

国内常规结构面形的“大汉”定日镜总面积100 m2，是由64块反射面积为(1.25×1.25)m2的子镜拼接而成[13]。以此为参照，选择整块定日镜中心4块子镜，即2×2结构模式，设定聚光焦距300 m,搭建了如图7所示的实验台进行模拟测量。子镜与光屏距离为3 m，凸透镜中心位于两者中间，且与实验台面的距离为0.5 m。

图7 定日镜测量实验台

以4块子镜拼接中心为坐标原点建立如图8所示的笛卡尔空间直角坐标系。其中H3为子镜理想法线，AB3为入射光线，B3F为反射光线。

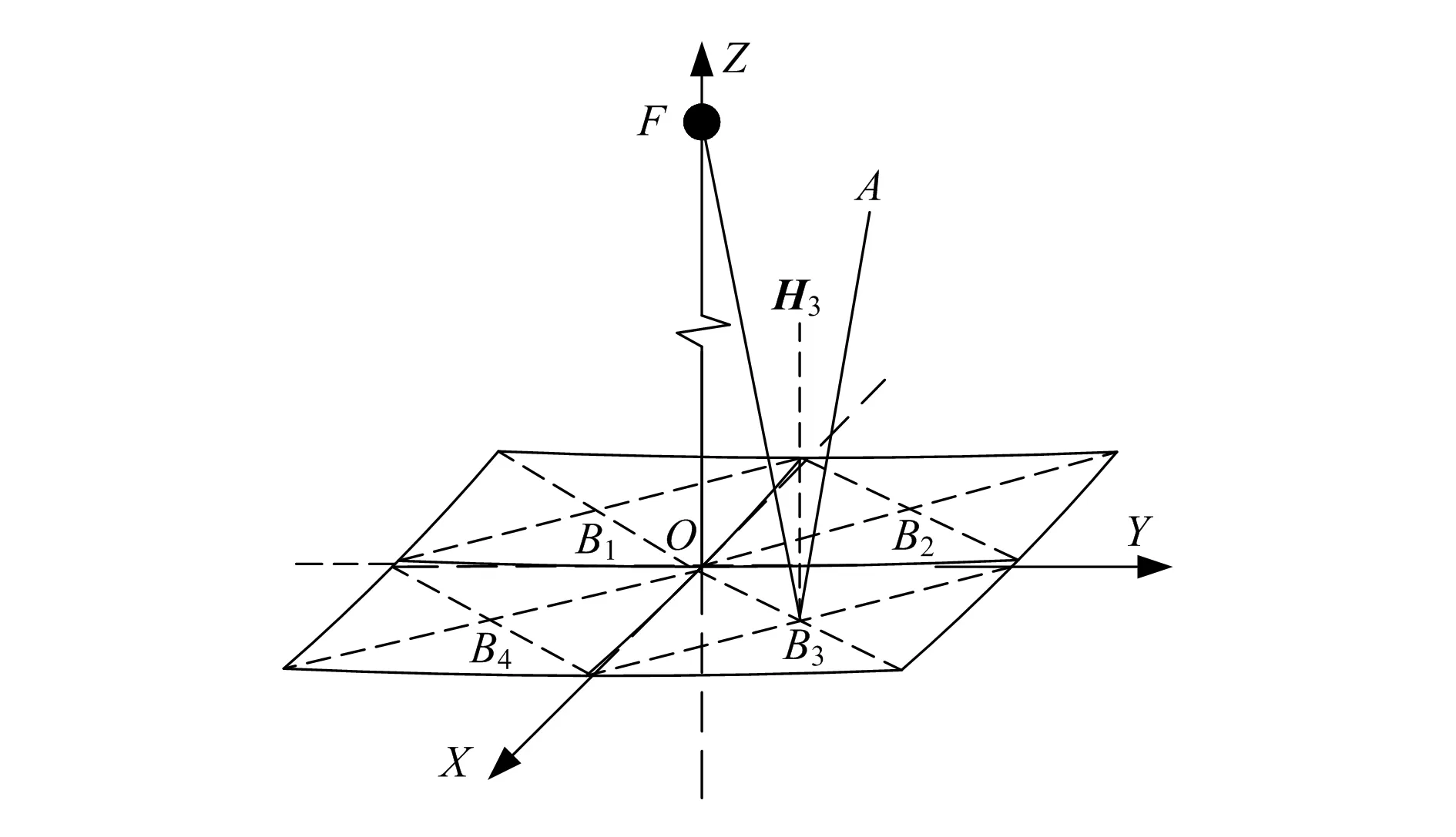
图8 子镜在单元镜坐标系的几何关系

由于每块子镜几何中心点都在抛物面x2+y2=4pz上，因此根据子镜边长确定几何中心坐标分布，见表1。

表1 “大汉”定日镜子镜坐标 mm

由于坐标系中子镜的几何中心均位于抛物面上，且同处于垂直OZ轴的截面上，故针对其中一块子镜进行检测、计算即可。在此选取坐标点B3(1 250,1 250,2.60)进行计算分析，将焦点坐标F(0,0,300)代入理想法线H′方向矢量的角轴关系式中可得：

(11)

因为子镜有效面形为正方形，所以X轴和Y轴坐标绝对值相等，等式变换的结果为B3子镜的理想法线方向矢量H′位于空间第三象限，偏离OZ轴5.83 mrad。

已知“大汉”定日镜镜面结构参数，经过坐标转换确定在检测模型坐标系中B3坐标为(1.250,1.250,-9.997)，通过实验台模拟检测D点在光屏上的落点坐标为(283,283,3 000)，由检测模型子镜法线矢量角-轴关系式(4)，在等式变换后得到子镜几何中心法线相对于OZ轴的偏角为6.95 mrad。

根据“大汉”定日镜300 m焦距位置的单元镜安装要求，每块子镜实际镜面法线与理想法线之间的最大误差允许角δmax为4.16 mrad，而在焦距300 m的距离上理想偏角和检测偏角差值为1.12 mrad，即小于最大误差允许角，满足要求。

4 结束语

本文在提出测量方法的同时还给出了检测原理的数学模型和理想平面度模型，可直接通过检测到的实际面形数据根据理想平面度进行面形参数调整。基于国外的激光束偏转法测量原理提出的针对大块拼接单元镜平面度参数的测量方法，相比于国内目前使用的相关检测方法具有检测速度快的优点，本文的研究可对发展国内塔式定日镜平面度检测起到了理论支撑作用。