基于视觉与惯性组合信息的图像特征提取与匹配

孙新成，刘胜兰，赵雪冬

(南京航空航天大学机电学院, 江苏 南京 210016)

图像特征提取与匹配属于机器视觉的基础研究内容，在位姿估计、三维重建、特征跟踪以及地图构建等应用中占据着重要的地位。目前常用的特征提取算法有SIFT[1](scale-invariant feature transform)、SURF[2](speeded-up robust features)、ORB[3](oriented FAST and rotated BRIEF)等，其中用SIFT和SURF算法提取的特征具有尺度、光照以及旋转不变性的优良性质[4]，但提取特征耗时长，难以在无人机导航定位、增强现实等实时性要求比较高的场合使用。而ORB算法由改进的FAST[5]检测子和二进制描述子BRIEF[6]组合而成，它不仅具有旋转和尺度不变的性质，而且能够缩短特征提取的耗时，满足实时性的要求，因此广泛应用于视觉即时定位与地图构建(vision simultaneous localization and mapping，VSLAM)等领域。但是在某些局部纹理丰富的场景下，采用ORB算法提取的特征会出现局部特征密集而造成特征冗余，从而影响特征点匹配的准确性且容易丢失大量图像信息。

在ORB特征点匹配过程中，由于噪声、遮挡以及图像中存在相似纹理等因素的影响易导致误匹配[7]。如果将错误的数据关联信息保留下来，将会导致后续运动估计的结果不精确或者失败，因此需要剔除掉误匹配的特征点，常用的误匹配剔除方法有距离阈值法、交叉验证法以及随机抽样一致(random sample consensus，RANSAC) 算法[7-8]等。距离阈值法操作简单，但是效果往往难以满足要求。交叉验证法是通过互换查询集和训练集来保证特征点匹配的唯一性，具有速度快、耗时少的优点，但是它并不能够完全剔除误匹配点对。RANSAC算法则是根据基础矩阵或单应性矩阵对初始匹配结果采用迭代方法找出最佳匹配点集，该算法能够有效地剔除误匹配，保证匹配结果的准确性，但是当初始匹配点存在较多的误匹配时，将会造成算法迭代次数过多，耗时较长，不满足实时性的要求。因此，可综合应用交叉验证法和RANSAC算法，既保证了匹配速度，又有较好的准确性。

目前，视觉与惯性测量单元(inertial measurement unit，IMU)组合在导航定位领域得到越来越多的应用，其可以将惯性导航仪获得的信息补充进来，进一步提高抽样一致性算法的效率。由于IMU与视觉传感器固联在一起，因此有相等的相对旋转矩阵。IMU包含加速计和陀螺仪两个组成部分，陀螺仪可以测得载体在运动过程中的三轴角速度的变化，通过对匹配图像帧之间的角速度测量值进行积分，获得匹配图像帧之间的旋转矩阵，从而只需要两组匹配点对就能够求解出基础矩阵[9]，降低RANSAC算法的迭代次数，加速误匹配剔除的速度。但是陀螺仪的测量值包含噪声和零漂，导致积分求解出的旋转矩阵与实际矩阵有偏差，将部分正确的匹配点对判定为误匹配，导致正确匹配点数量较少。

针对上述存在的问题，本文工作如下：1)针对ORB特征的冗余现象，基于网格化思路，采用改进的ORB特征算法[10]去除冗余特征，保证提取的特征在图像上分布均匀；2)采用暴力匹配方法获得相邻图像帧的粗匹配结果，通过交叉验证法对初始匹配进行过滤，保证特征匹配的唯一性，再结合陀螺仪的先验信息，采用两点RANSAC算法获得正确匹配点集，然后根据该匹配点集来重新计算本质矩阵，并获得在该本质矩阵下的匹配特征点,最后设计实验对本文算法进行了验证。

1 基于网格划分的ORB算法改进

ORB算法分为关键点和描述子两部分，其中关键点采用改进的FAST角点，通过灰度质心法[3]使得ORB特征具备旋转不变形，同时对原始图像进行降采样构建图像金字塔并在每一层图像上检测角点，以保证ORB特征具有尺度不变性。但是ORB算法在特征提取过程中采用统一的阈值，而且对所有特征采用非极大值抑制处理，容易造成角点分布不均、特征冗余现象。

为了消除传统ORB算法存在的特征冗余问题，本文首先采用网格化方法提取特征，然后基于四叉树数据结构对所提取的特征点进行过滤，最后将过滤后的特征点输出。网格化是将图像按照一定的尺寸进行分块处理，使每一个小块区域能够自适应地选取角点，提取阈值，从而保证每一小块区域都能够提取到足够多的特征点。自适应阈值的选择标准是：首次以最大阈值进行特征提取，如果没有提取到特征，则以较小的阈值进行特征提取，当完成所有区域的特征提取后，再基于四叉树结构对局部区域的冗余特征进行剔除，流程如图1所示。

图中，树根L0层表示初始提取的特征点在图像上的分布位置，Ln层表示第n次的划分结果，具体的操作步骤如下。

图1 基于四叉树结构的特征点筛选

Step1，将L0层即根节点中所有特征点按照像素坐标位置分成4组，分别对应L1层的4个节点。

Step2，统计L1层每个节点的特征点数量，如果该节点的特征点数量为1，则该节点不参与划分；如果该节点的特征点的数量为0，则直接将该节点从树结构中删除；如果该节点中包含的特征点数量大于1，则将该节点中的特征点按照图像坐标位置进行4等分划分。当L1层中的所有节点执行完上述操作后即可以得到L2层，后续采用迭代的方式对L2，L3，…,Ln-1层执行相同的操作。

Step3，当满足下面3个判断条件中的任意一个时则迭代循环结束：1)Ln层不存在特征数量大于1的节点；2)Ln层的最小边界尺寸小于5个像素(保证不会出现局部特征密集现象)；3)Ln层的所有节点个数加上L1～Ln-1层没有孩子的节点个数大于或等于设定的特征点数量。

Step4，若是第1)种情况，直接返回特征数量为1的节点，并输出对应特征点；若是第2)种和第3)种情况，对Ln层中特征点数量大于1的节点采用非极大值抑制的方法进行特征筛选，只保留Harris响应值[11]最大的特征点，然后同样输出特征数量为1的节点。

2 传统RANSAC算法

采用改进的ORB算子对两帧图像进行特征提取，然后通过暴力匹配方法计算第一帧图像中每一个特征点的描述子向量与第二帧图像中所有特征点的描述子向量的汉明距离，汉明距离值越小表明两个特征点越相似，将汉明距离值最小的一组判为匹配点。然而由于噪声、遮挡以及图像纹理相似性等因素的影响，初始匹配点集中存在错误匹配的点对，需采用RANSAC算法进行误匹配剔除。

传统RANSAC算法通常基于基础矩阵采用八点对法[12]进行迭代求解，具体的求解步骤如下：

Step1，从初始匹配点集中随机抽取8组匹配点。

Step2，根据两视图的对极几何性质，采用Step1中抽取的8组匹配点构建的线性方程：

(1)

(2)

式中：K为相机的内参矩阵；E为本质矩阵，只与两帧图像之间的旋转矩阵R和平移向量t有关；[·]×为叉乘算子。在本文应用场景下相机内参矩阵K已离线标定，因此采用奇异值分解法(singular value decomposition，SVD)求解本质矩阵E。

Step3，根据Step2中求解出的本质矩阵E，对初始匹配点集中所有特征点进行内、外点判断，得到满足该本质矩阵E的一致集(内点集)。内、外点的判定条件为：

(3)

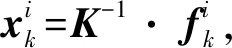
Step4，统计Step3求出的一致集的内点数量，判断它是否为最优一致集，如果是，则更新当前最优一致集，否则不更新。

Step5，判断是否满足迭代终止条件，若满足，则退出迭代循环并输出最大内点集，否则跳到Step1继续执行。迭代过程中置信度设置为p，匹配集中内点所占的比率为w，w等于每次迭代过程中最优一致集的内点总数/初始匹配集中匹配点对总数，迭代更新时每次抽取样本的个数为k，则在该置信度下所需要的迭代次数N可以通过下式计算：

(4)

式中：传统RANSAC算法中k设置为8。

3 改进的误匹配剔除算法

针对暴力匹配法获得的初始匹配点集存在较多误匹配点对，导致RANSAC算法迭代的次数明显增加的问题，有两种加速算法迭代速度的解决方法，一是对初始匹配点集进行粗剔除，降低外点比例；二是降低每次抽取样本的特征点个数。本文采用组合方法由粗到精地剔除外点，提高误匹配剔除的效率。首先采用交叉验证法进行粗剔除，然后采用两点RANSAC方法进行精剔除，最后根据精剔除后的内点重新估计本质矩阵，从匹配点集中筛选出满足该本质矩阵的一致集，并输出本质矩阵和正确匹配的特征点。

3.1 交叉验证法粗剔除

交叉验证法首先以第一幅图像帧F1中的特征点作为查询集，第二幅图像帧F2中的特征点作为训练集，完成两帧图像之间的特征点匹配，如图2中实线箭头所示；然后以F2中的特征点作为查询集， F1中的特征点作为训练集，得到两帧图像特征点的匹配关系如图2中虚线箭头所示；最后将两次匹配结果一致的判定为内点，否则为外点。匹配示意图如图2所示。

图2 交叉验证法示意图

从图中可知，特征点1的两次匹配结果不一致，因此采用交叉验证法将特征点1判定为外点，从而保证图像帧F1与F2中特征点匹配的唯一性。但是对于特征点4和特征点5的误匹配现象，则无法通过交叉验证法对其进行剔除，针对这样的问题，本文接下来将采用改进的两点RANSAC算法进行精剔除。

3.2 两点RANSAC算法

传统RANSAC算法在迭代过程中每次需要随机抽取8组点对，但本文应用场景只需要抽取2组匹配点对。由于通过对匹配图像帧之间的陀螺仪测量值积分可计算出IMU旋转变换矩阵，而IMU传感器和相机固联在一起，因此相机和IMU在运动过程中满足下列关系：

(5)

(6)

式中：exp(·)表示旋转向量到旋转矩阵的指数映射关系；n为匹配图像帧之间的角速度测量数据个数；bg为陀螺仪的零漂，可通过离线标定；Δt为采样时间间隔。在获得匹配图像帧之间的旋转矩阵后，考虑对极几何约束关系，将匹配集中的一组匹配特征点x1,x2投影到单位球面上，得到单位化坐标向量p1,p2，有‖p1‖=‖p2‖=1，如图3所示。

图3 对极几何约束关系

(7)

图4 平移变换

t=r[s(θ)·c(φ),s(θ)·s(φ),c(θ)]T

(8)

式中：s(·)和c(·)分别表示三角函数sin、cos；θ为方位角；φ为极角；r为平移向量的模长，即球坐标的径向距离。r取任意非零常量并不改变式(7)的约束关系，因此在实际工程中通常对其进行归一化处理，即令r=1。则本质矩阵E′为：

E′=[t]×=

(9)

p0,p2的坐标分别为[x0,y0,z0]T和[x2,y2,z2]T，结合式(7)和(9)可将对极约束方程展开成如下形式：

(y2c(θ)-z2s(θ)s(φ))x0+(-x2c(θ)+z2s(θ)c(φ))y0+(x2s(θ)s(φ)-y2s(θ)c(φ))z0=0

(10)

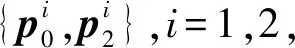
(11)

为了便于表达，在式(12)中定义了中间变量a,b,c,d,e,f：

(12)

求解出θ,φ值后，将其代入式(9)计算出E′矩阵，则初始匹配图像帧的本质矩阵为：

(13)

由此可见，两点RANSAC算法降低了迭代过程中每次抽取样本时所需的特征点对个数，达到减少迭代次数、加速算法收敛速度的目的。

3.3 外点精剔除

结合陀螺仪先验信息获得匹配图像帧之间的旋转矩阵，采用两点RANSAC算法提高误匹配剔除效率。但是陀螺仪测量的数据存在噪声，在实际误匹配剔除过程中，采用两点RANSAC算法会将部分正确的匹配点判定为外点，导致内点的数量明显减少。针对这样的问题，本文对两点RANSAC算法获得的匹配结果重新估计本质矩阵，从而获得精确的本质矩阵，再从初始匹配点集中寻找该本质矩阵的最大一致集。

(14)

其中

e=[e11,e12,e13,e21,e22,e23,e31,e32,e33]

(15)

式中：e11,e12,…,e33为本质矩阵中的元素，下标表示各元素在本质矩阵中的坐标。

将式(14)简写为Aie=0，其中Ai表示式(14)左边1×9的矩阵，e表示由本质矩阵中的元素构成的9维向量，则对Sn点集采用式(14)计算可获得n个等式，表示为：

Ae=0

(16)

式中：A是由Ai构成的n×9矩阵，A矩阵的秩为8。通过对ATA矩阵进行SVD分解，得到其最小特征值所对应的特征向量即为本质矩阵E，然后根据第2节中Step3计算出满足该本质矩阵的最大一致集，即为正确匹配结果。

4 实验结果分析

本文实验采用Windows10 64位操作系统，Intel(R) CoreTM i3-3240 CPU @ 3.4 GHz, 8 GB内存，运行环境为Visual Studio 2017平台，并基于开源计算机视觉库(OpenCV)编写C++程序。采用的视觉惯性数据采集设备为MYNTAI公司的小觅双目摄像头，它集成了一个六轴IMU传感器和全局曝光的双目摄像头。实验过程中将相机的采集帧率设置为20 fps，相机采集的图像为单通道灰度图像，分辨率为752像素×480像素；IMU传感器的采集频率设置为500 Hz，可以测得载体自身三轴加速度和三轴角速度值。实验数据分别通过手持摄像头和无人机机载方式采集，其中无人机飞行速度为3 m/s,飞行高度为10 m。

4.1 特征提取实验

针对本文改进的ORB算法进行实验测试时，将传统ORB算法和改进ORB算法的特征筛选阈值都设置为20，而改进ORB算法二次筛选阈值设置为10，实验提取的特征数量设置为500，图像金字塔层数设置为3，金字塔图像之间的尺度参数设置为1.2。特征点的提取结果如图5,6所示，图5为室内楼道场景的特征提取结果，图6为花坛场景的特征提取结果。

图5 楼道场景特征提取结果

图6 花坛场景特征提取结果

由图5,6可知，采用传统ORB算法提取角点时出现特征冗余，而采用改进ORB算法提取的角点分布均匀，有效地避免了特征冗余。对于特征提取耗时，通过1 000次实验求平均值方式进行统计，特征提取的耗时结果对比见表1。由表可知，改进ORB算法在特征提取耗时相比原算法仅增加了5 ms，依然能够保证ORB算法的实时性能。

表1 不同算法的特征提取耗时 ms

4.2 误匹配剔除实验

为验证改进误匹配剔除算法剔除外点时的性能，本文首先采用改进的ORB算法提取特征点，接着采用暴力匹配法(BF)对特征点进行匹配，获得初始的匹配结果，然后分别采用交叉验证法、传统RANSAC算法、交叉验证法与传统RANSAC组合算法以及本文算法进行外点剔除实验。RANSAC算法的初始迭代次数都设置为1 000，置信度设置为0.99，阈值δ设置为1.5像素，匹配图像帧采样频率为1 Hz,实验结果如图7,8所示，图7和图8的三轴角度变化值分别为(-23.602°，2.143°,6.286°)、(0.088 5°，-0.123 3°，-0.039 8°)。

图7 楼道场景下的不同算法获得匹配结果

图8 花坛场景下的不同算法获得匹配结果

由图7,8可知，交叉验证法虽然能够保证特征点匹配的唯一性，但是仍存在着大量误匹配。相比较而言，其他3种算法都能有效地剔除外点，其中传统RANSAC算法还存有少量误匹配点，而交叉验证法+传统RANSAC算法和本文算法基本无外点存在，保证了特征匹配的正确性，为后续的位姿估计或三维重建等提供可靠的数据关联关系。对上述不同算法的耗时和内点数量进行了统计，结果分别见表2和表3。由表2,3可知，交叉验证法+传统RANSAC算法的耗时比传统RANSAC算法少，表明采用交叉验证法进行粗剔除能够有效地减少算法迭代耗时；本文算法的耗时最少，表明两点RANSAC算法能够有效地减少耗时，验证了本文算法的可行性和鲁棒性。

表2 楼道场景下不同算法的匹配结果

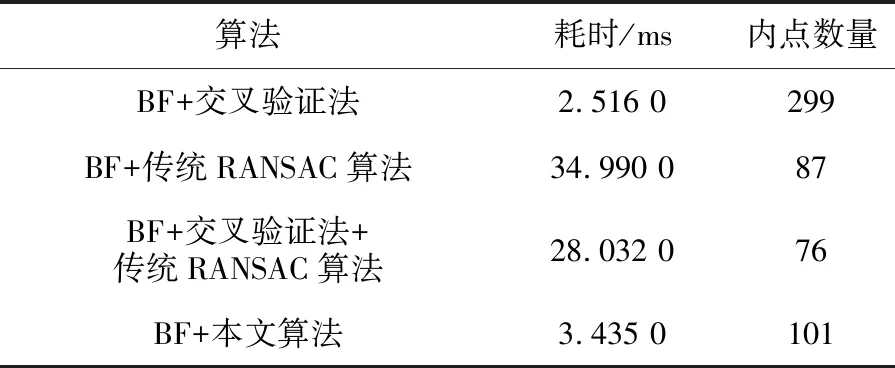
表3 花坛场景下不同算法的匹配结果

为了避免偶然因素的影响，本文对无人机飞行过程中采集的100帧图像进行不同算法性能对比实验，采样频率为5 Hz。首先采用改进ORB算法进行特征提取，接着采用暴力匹配法对特征点进行匹配，然后分别采用传统RANSAC算法、交叉验证法+传统RANSAC算法和本文算法获得匹配结果，交叉验证法获得的结果外点过多不参与评估，最后对不同算法的匹配耗时和内点结果进行统计分析，结果见表4，绘制的不同算法耗时和内点数量曲线如图9和图10所示。

表4 连续100帧图像不同算法的匹配结果

图9 不同算法的耗时曲线

图10 不同算法的内点数量曲线

由图9可知，本文算法的耗时明显少于另外两种算法；由图10可知，本文算法获得的内点数量和交叉验证法+传统RANSAC算法几乎一致，都能够有效将误匹配的点对进行剔除并获得足够多的正确匹配特征点。由表4可知，本文算法平均耗时只有传统RANSAC算法的1/10，是交叉验证法+传统RANSAC算法的1/5，验证了本文算法的鲁棒性和实时性。

5 结论

本文采用改进的ORB算法结合由粗到精的误匹配剔除算法，对基于视觉惯性传感器采集的图像进行特征点的提取与匹配，得到以下结论：

1)采用基于网格化的ORB改进算法进行特征点的提取，可以有效地减少特征的冗余。

2)针对初始匹配点存在的大量误匹配点对，本文提出的由粗到精的误匹配剔除算法，保证了算法的运行速度，且有较好的匹配准确度。

3)实验结果表明，本文算法能够获得与传统RANSAC算法相同的匹配结果，且耗时只有传统RANSAC算法的1/10，说明本文算法有较好的鲁棒性和实时性。