轴承误差与弹性变形对斜齿轮传动精度的影响分析
董惠敏,步 鹏
(大连理工大学机械工程学院, 辽宁 大连 116024)
斜齿轮传动因其具有传动效率高、结构紧凑等特点,被广泛应用在各种传动场合。一个完整的齿轮传动系统由齿轮、轴、轴承等零部件组成,这些零部件在应用中不可避免地会存在制造误差和弹性变形,通过在动静联结面之间的相互传递,最终反映在齿轮轴的六自由度误差运动上,导致齿轮轴出现浮动效应,因而这些制造误差和弹性变形对传动误差的影响是不可忽视的[1]。现有对齿轮传动精度的研究,多分析齿轮本身参数[2]或者齿轮误差因素对传动精度的影响,如齿轮安装误差[3- 4]、齿轮制造误差[5-6]、齿轮弹性变形[7]等,有些学者[8- 9]考虑了轴承的弹性变形,但未考虑轴承滚道误差对传动精度的影响,因而难以较真实地等效出斜齿轮传动系统的真实运动状态。对于误差条件下的齿轮弹性变形的计算,大多采用有限元法[10]或者有限元法与解析法相结合的方法[11],存在计算效率低且建模过程复杂的不足。
本文建立了可综合考虑轴承误差和弹性变形的斜齿轮传动的精度分析模型,从而将斜齿轮在轴系运动误差下的复杂空间接触问题转化为一系列截面内的直齿轮平面接触问题。
1 斜齿轮传动系统精度分析模型
1.1 模型描述
以图1所示的斜齿轮传动系统为例,根据其结构特点,建立如图2所示的斜齿轮传动系统等效模型。模型将轴承滚道径向和轴向的圆度误差分别等效映射到一个刚性的盘状凸轮的轮廓面和端面上,凸轮与齿轮轴的连接点为凸轮的几何中心,一根轴上两凸轮的距离为实际轴承支撑几何中心的距离,即轴承支撑段中心截面的距离。对于轴承的刚度,用凸轮从动件上的复位弹簧来等效,从动件末端的位移量表示弹簧的形变量,根据角接触球轴承的约束形式,每个凸轮配有5个弹簧来约束其相应方向上的自由度,弹簧只受压不受拉。为了分析误差条件下齿面间隙分布和齿轮的弹性变形情况,将斜齿轮沿齿宽方向离散为一系列等厚度的薄片,当薄片的厚度很小时,斜齿轮可近似看作是由一系列相差了一个相位角的薄直齿轮组成[12]。
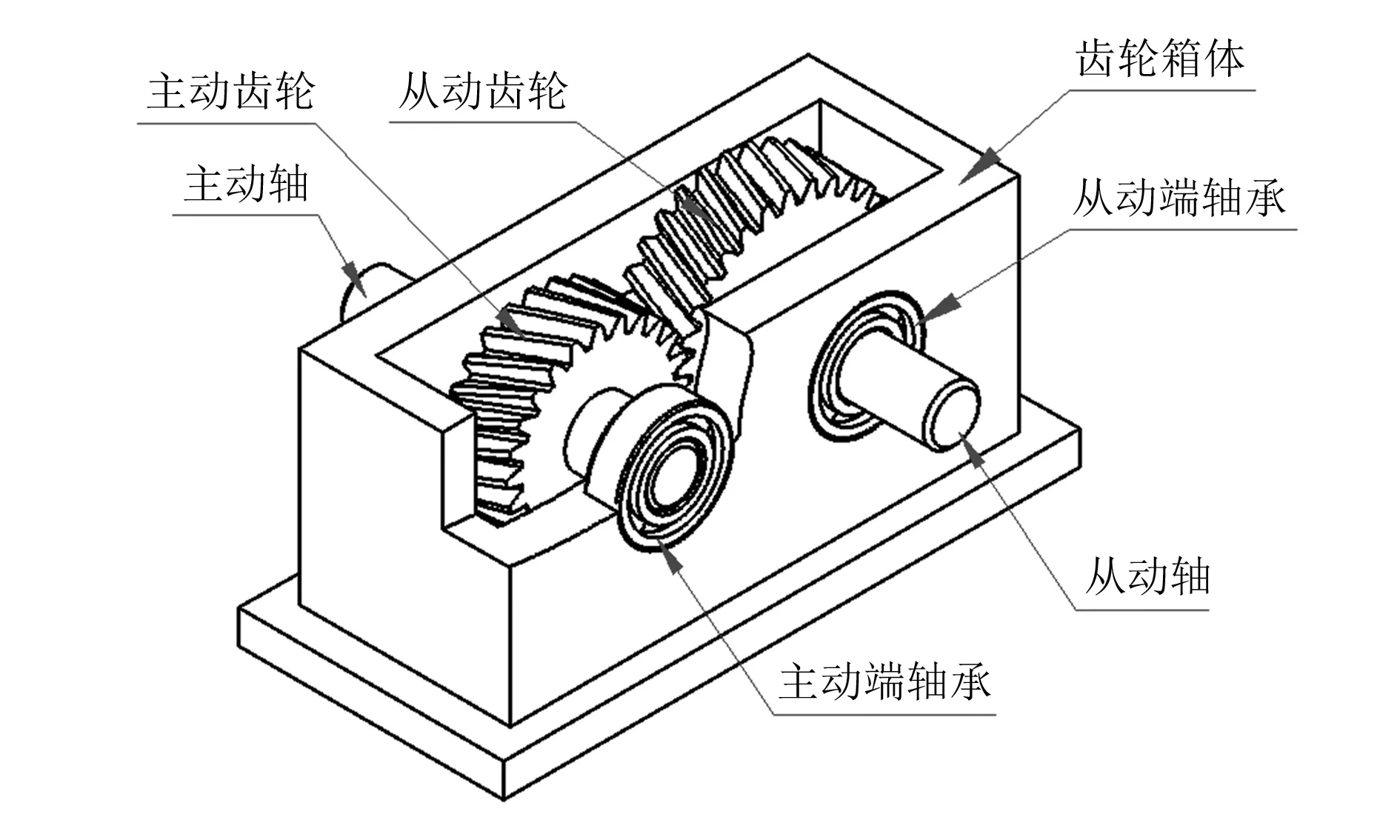
图1 斜齿轮传动系统简图
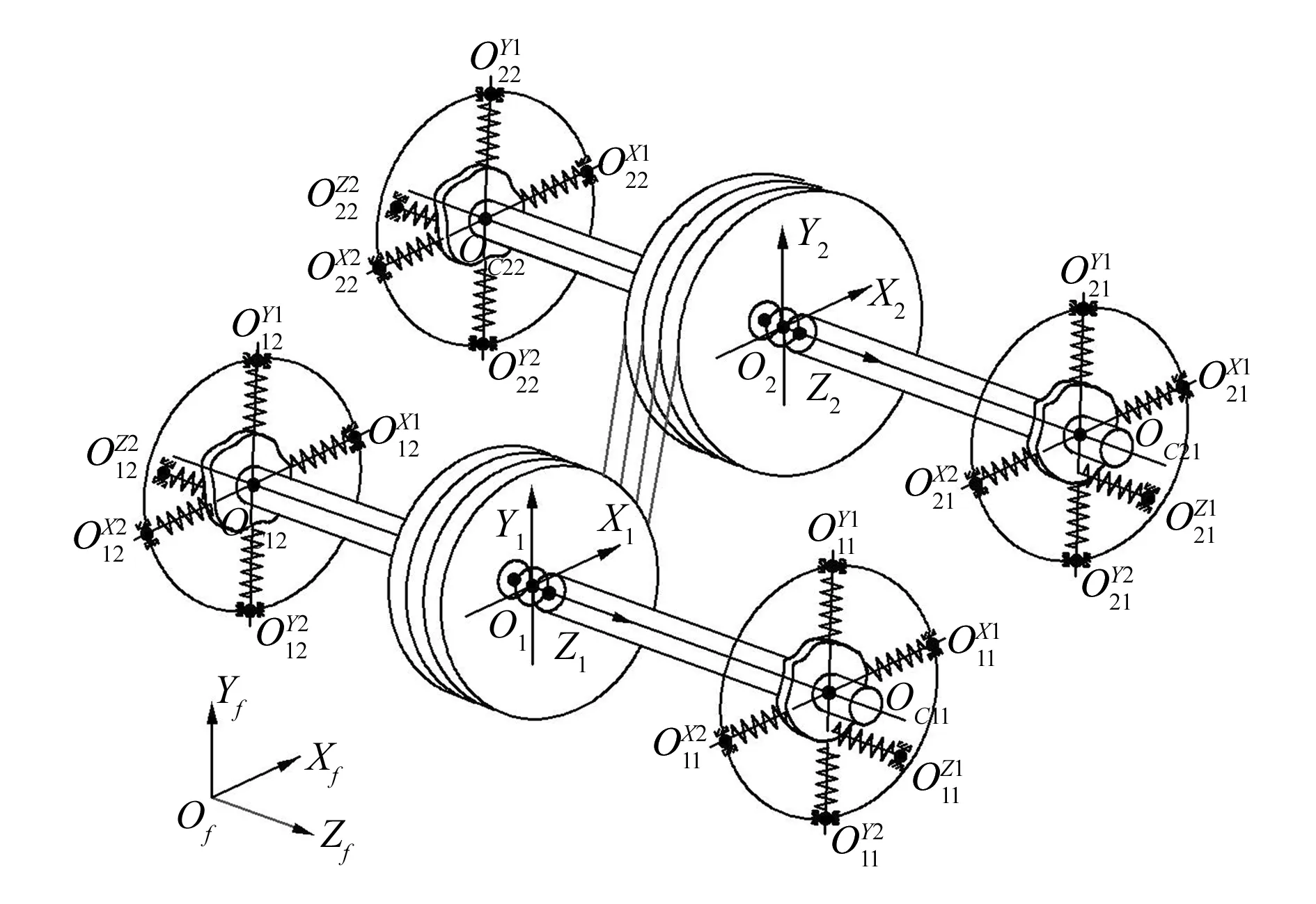
图2 斜齿轮传动系统等效模型
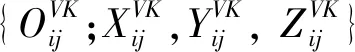
1.2 模型参数定义
含制造误差的轴承滚道形状是理想圆和圆度误差的叠加,可以用凸轮轮廓R(θ)来等效表达,在凸轮坐标系中用傅里叶级数拟合表示:
(1)
式中:D为轴承内圈滚道的理论直径;EN为轴承圆度误差的第N阶谐波分量系数;N为误差阶次;θ为误差位置角;ψN为误差初始相位。
凸轮从动件弹簧的刚度是轴承在各方向上的结构刚度kVKij,本文采用有限元法计算得到的轴承径向和轴向刚度拟合曲线如图3所示。
每一个直齿轮薄片的啮合刚度k由轮齿的弯曲刚度kb、剪切刚度ks、基体刚度kf、径向压缩刚度ka以及接触刚度kh组成,薄片齿对的单齿啮合刚度可通过势能法[13]计算:
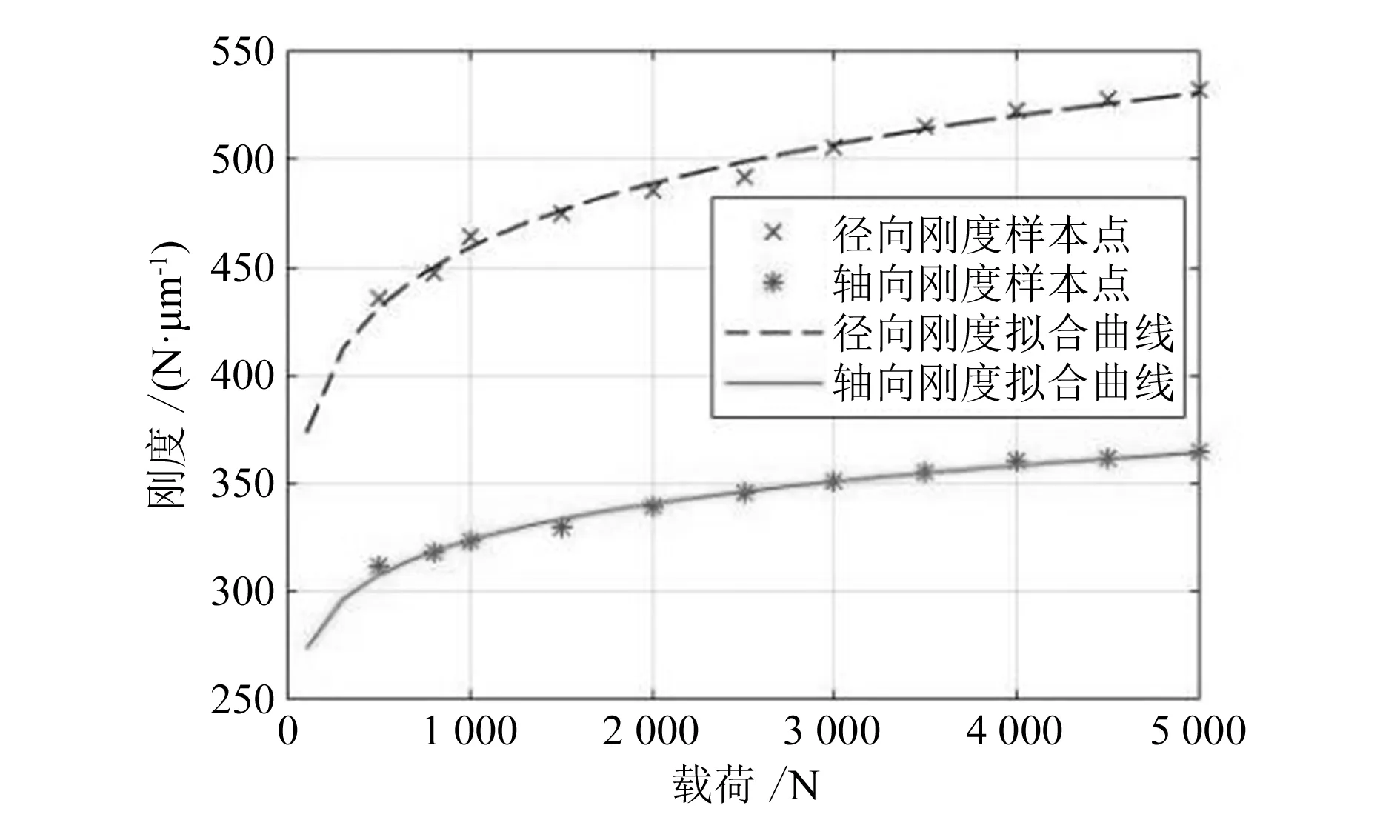
图3 轴承刚度与载荷关系的拟合曲线
(2)
式中:下标1,2分别表示主动轮和从动轮;下标n为薄片齿对的编号。
2 模型基本方程
2.1 齿轮薄片位置

(3)
(4)
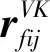
如图4所示,对于每个凸轮从动件,根据凸轮与从动件的位置关系和系统的结构参数,由几何关系可得每一个从动件对应的位移矢量闭环方程:
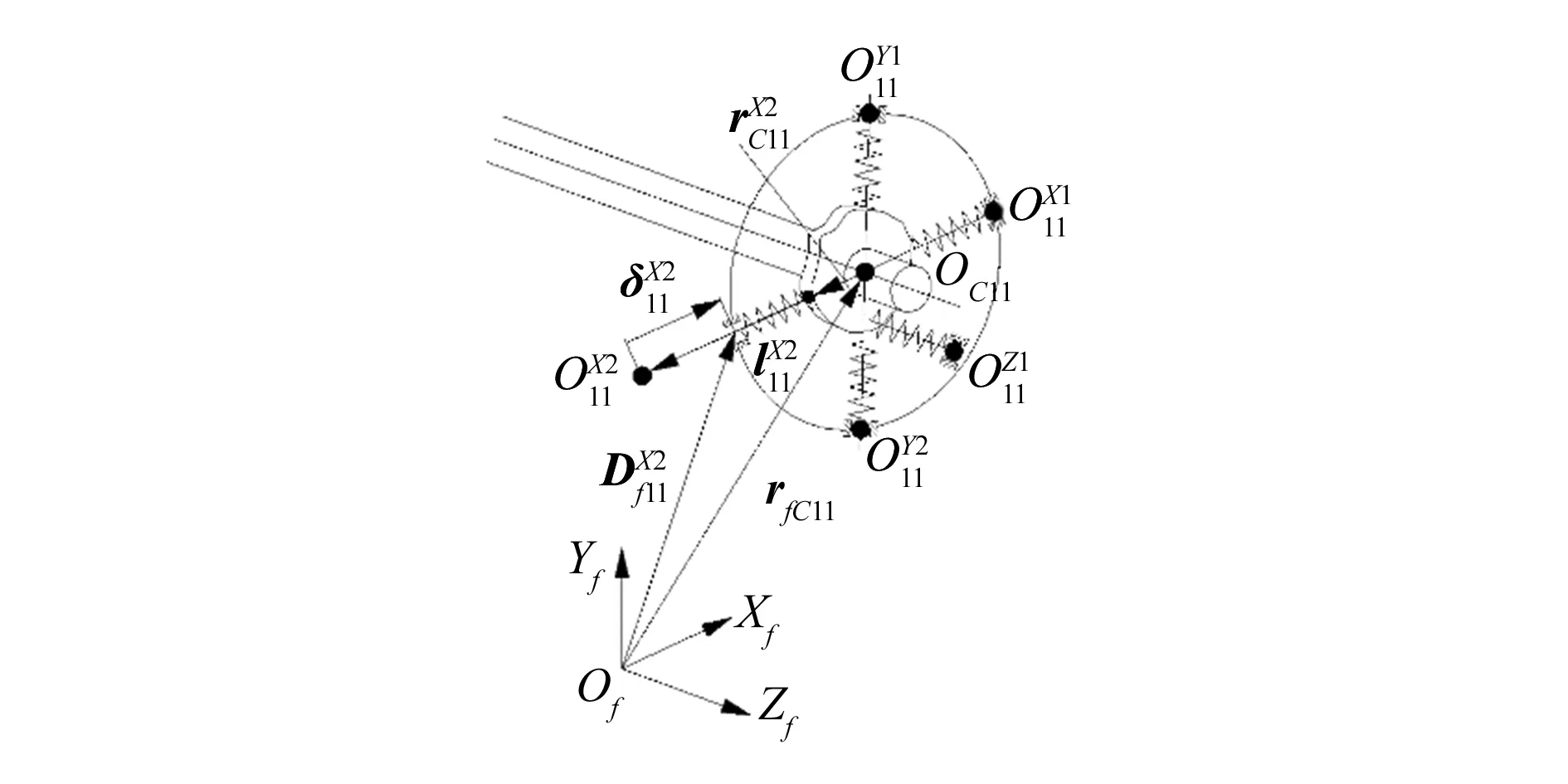
图4 从动件位移矢量示意图
(5)
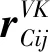
(6)
(7)
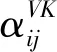
通过联立方程(3)~(7),可以求解出模型中齿轮在任一转角位置时凸轮与从动件的位移参数。式(5)中的rfCij表征各凸轮几何中心在全局固定坐标系下的位移情况,由此可确定轴i上与凸轮1距离为l的任意点在全局固定坐标系下的位置rfi为:
(8)
式中:L为轴承的跨距。
2.2 齿面间隙
如图5所示,轴承的误差和弹性变形会导致齿轮轴线的偏斜,导致原本应该相互啮合的齿面彼此分离或嵌入,且每一个薄片齿对的间隙都不一样。为了分析间隙在薄片齿对间的分布情况,以每一个薄片齿对的中间截面为分析对象。由于轴线偏斜误差量一般较小,假定在截面内两齿轮齿廓仍保持渐开线形状,为了便于分析,在齿轮薄片1n的基圆圆心建立坐标系S1n,利用坐标变换将齿轮薄片2n的基圆圆心的位置表达在坐标系S1n下的坐标r12n为:
r12n=rf2n-rf1n
(9)
式中:rf1n和rf2n分别为齿轮薄片1n和2n基圆圆心在全局固定坐标系下的矢径。
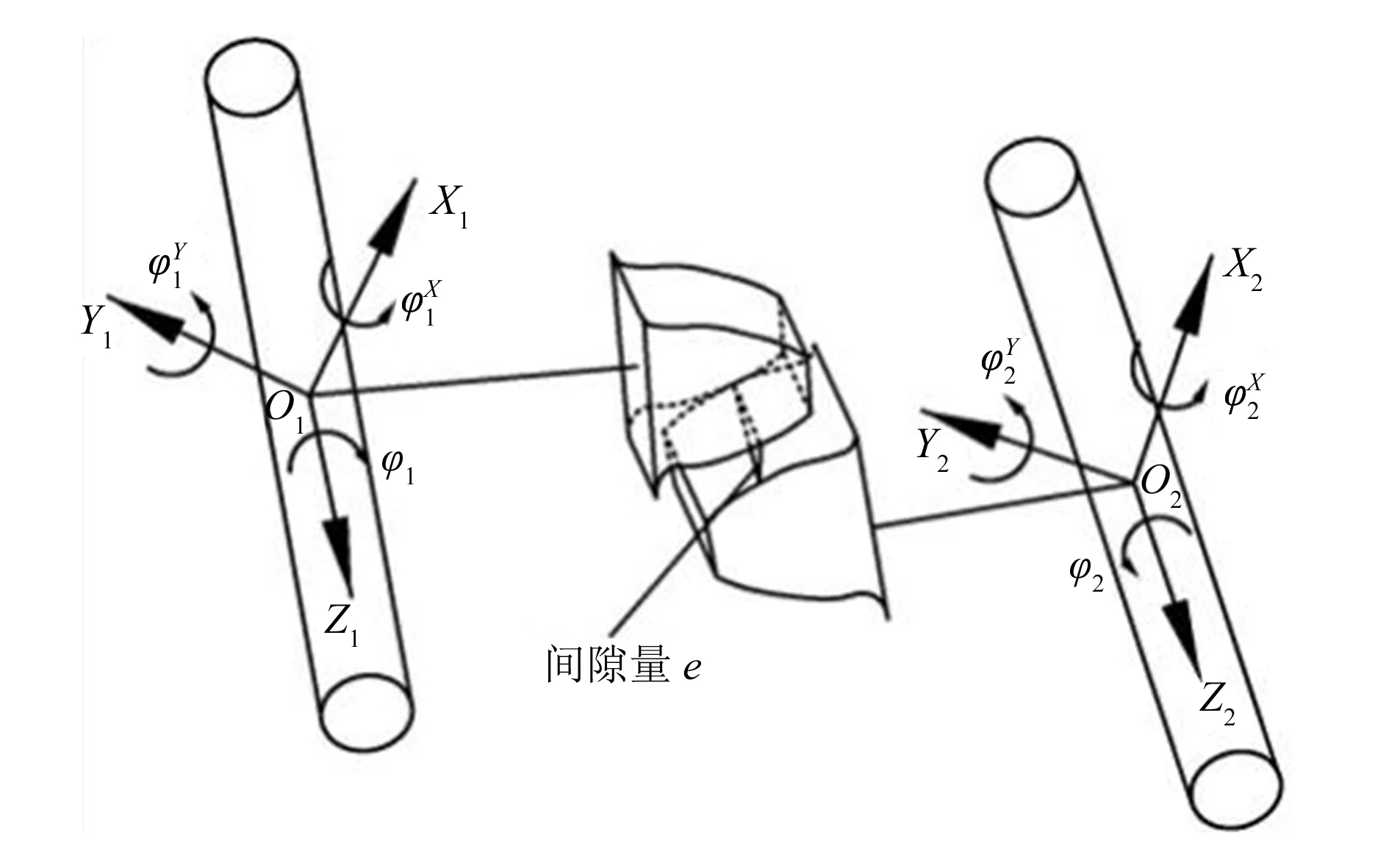
图5 齿面间隙分布示意图

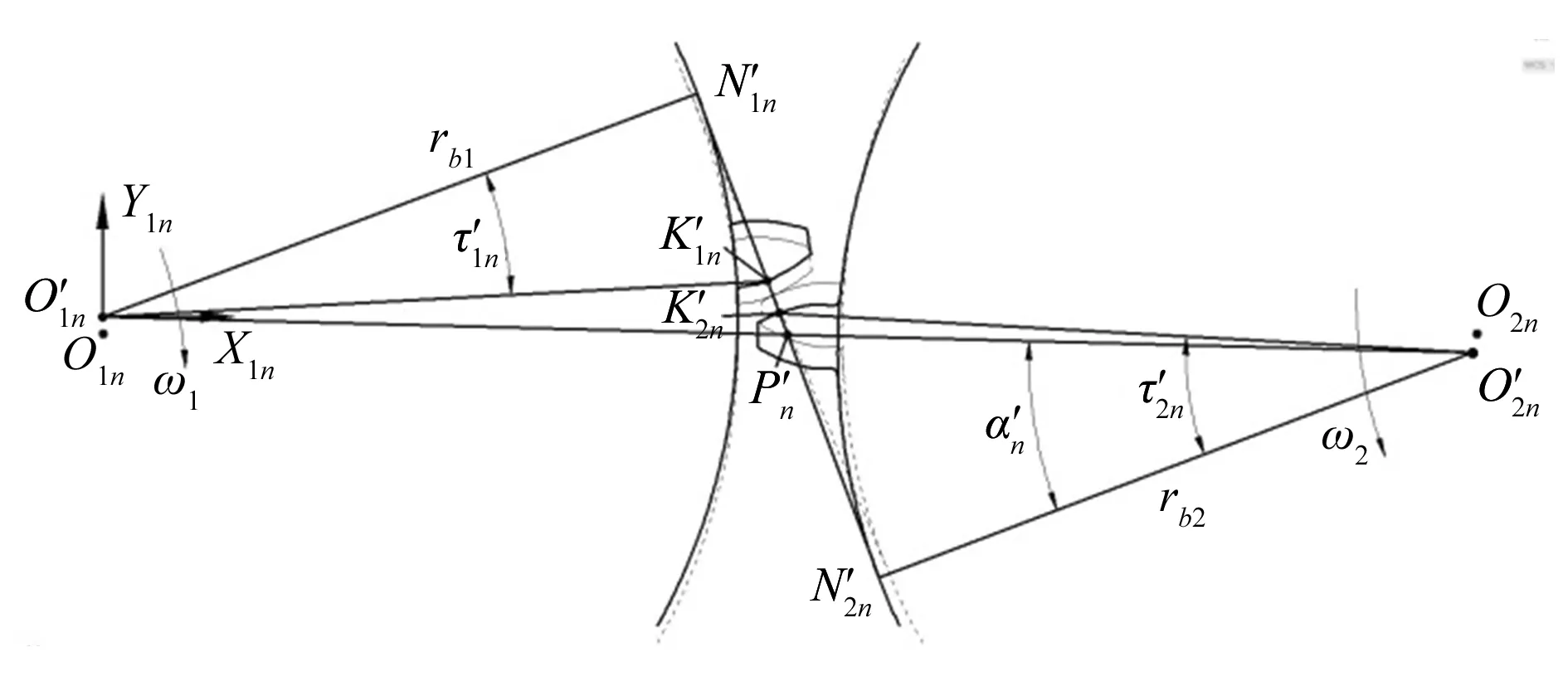
图6 薄片齿对间隙计算参数示意图

(10)
(11)

(12)

(13)
2.3 齿轮弹性变形
轮齿在误差条件下的啮合过程如图7所示,每一根弹簧代表一个薄片齿对,承载前各薄片齿对均存在间隙,承载后,在载荷的作用下,间隙最小的薄片齿对m先接触并变形,当此齿对的形变量δm与间隙量em之和大于齿对n的间隙量en时,齿对n开始接触并承载,以此类推,直至所有参与接触的薄片齿对产生的承载量的和等于外载荷F。

图7 齿轮承载接触过程
根据齿轮承载前后的变形协调关系,齿轮承载后沿啮合线方向的综合位移量E可表示为:
E=δm+em=en+δn
(14)
即任意薄片齿对n的形变量δn大小为:
δn=δm+em-en
(15)
若δn≥0,则说明齿对n接触,令其刚度等于kn。若δn<0,则说明齿对n未接触,令其刚度等于0。
2.4 传动误差求解
根据以上建立的数学模型进行编程计算可求出误差条件下齿轮传动误差大小,传动误差的求解流程如图8所示。

图8 传动误差计算流程图
3 算例分析
以图1所示的斜齿轮传动系统为分析对象,研究轴承滚道圆度误差和刚度对齿轮传动误差的影响规律,所有轴承的型号均为7213AC,齿轮变位系数为0,齿轮轴系的基本参数见表1。
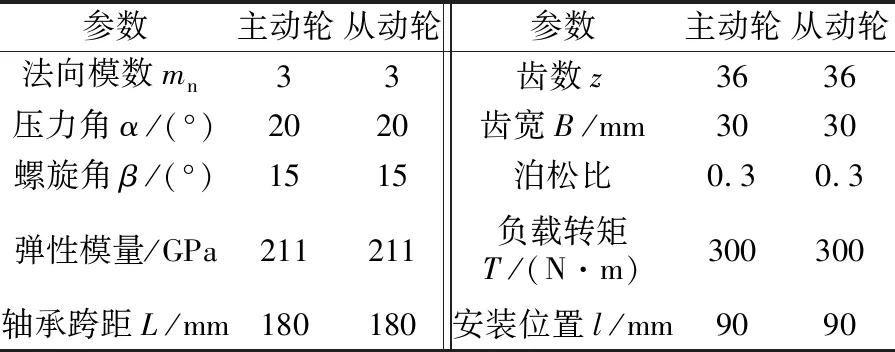
表1 齿轮轴系的基本参数
3.1 轴承精度对传动误差的影响
不同精度等级的轴承对应滚道的圆度误差大小也不同,分析模型中轴承精度等级分别为6级、5级和无误差时传动误差的变化情况,主动轮两轴承相位差为π/2,从动轮两轴承相位差为0,误差阶次都为1阶,结果如图9所示。
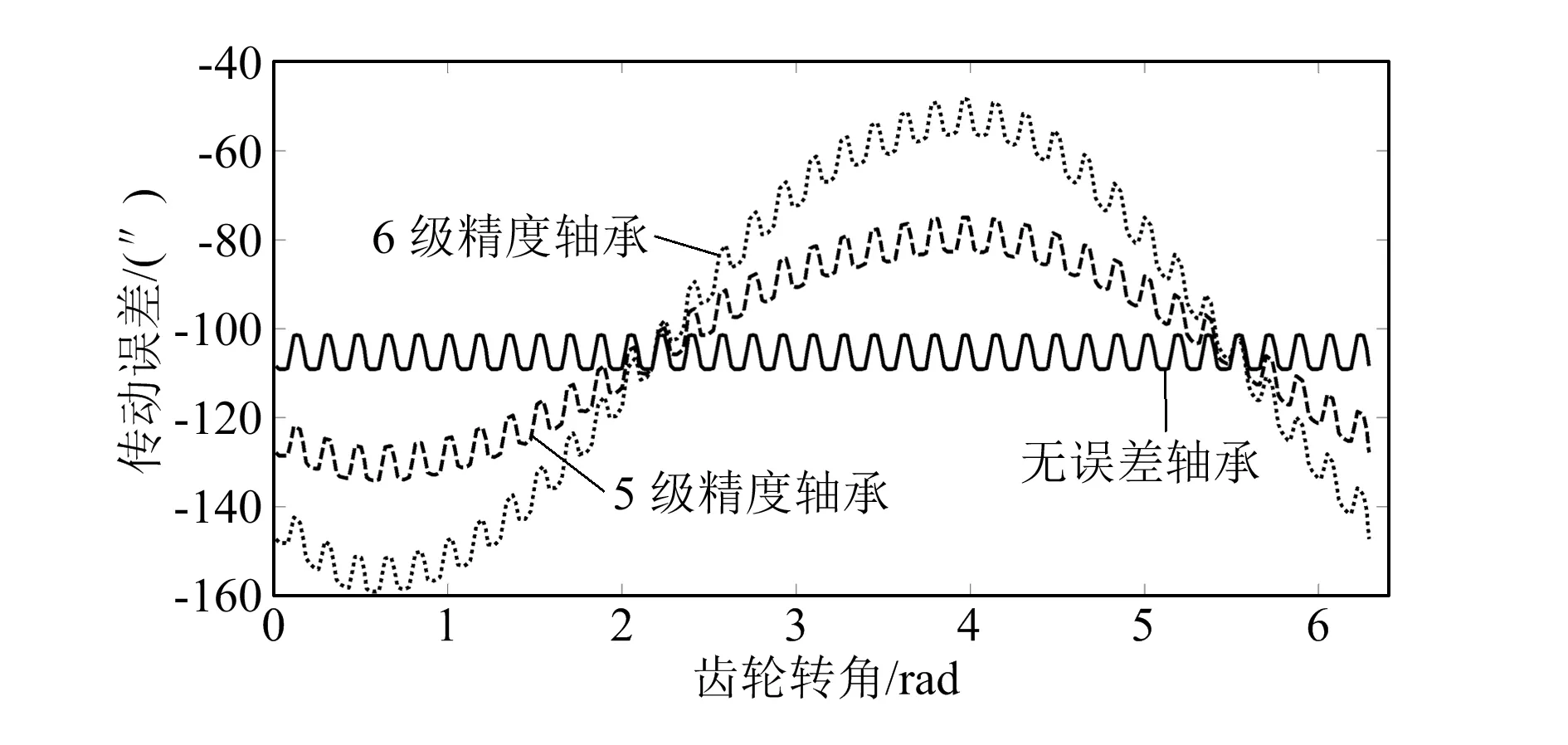
图9 轴承精度对传动误差的影响
由图9可知,传动误差呈现出由时变啮合刚度导致的小波动和由轴承滚道误差导致的大波动相叠加的周期性波动的形式,轴承精度不影响传动误差大波动的相位和频率,但是随着轴承精度的降低,传动误差大波动的幅值逐渐变大。
3.2 轴承滚道圆度误差相位对传动误差的影响
为了分析轴承滚道圆度误差相位对传动误差的影响规律,令从动轮轴系两端轴承相位差为0不变,改变主动轮两轴承相位差ψ分别为π/2和π,轴承精度为6级,误差阶次为1阶,计算结果如图10所示。
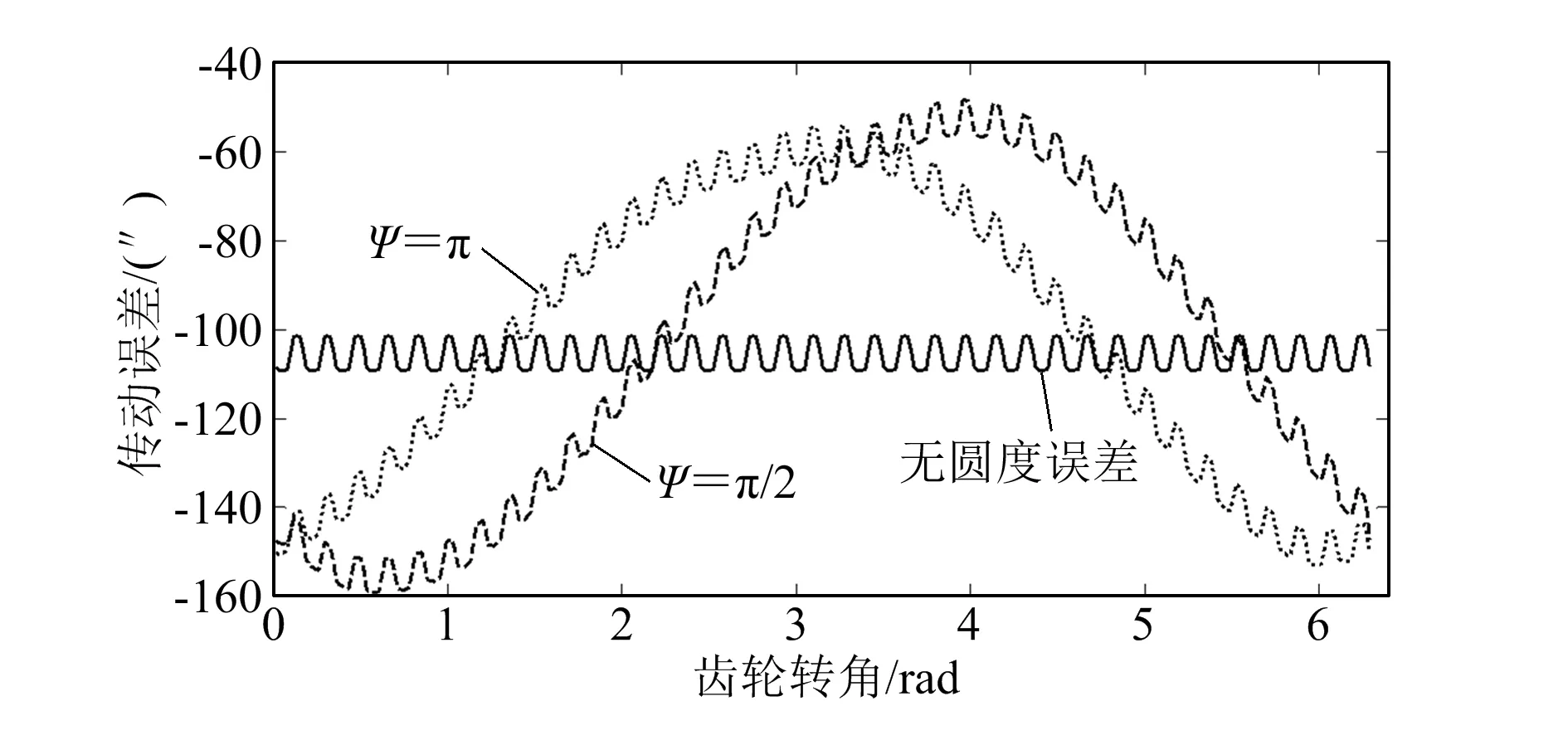
图10 轴承滚道圆度误差相位对传动误差影响
由图10可知,轴承滚道圆度误差的相位并不影响传动误差大波随齿轮转角变化的频率,但是会改变大波的相位和幅值大小。
3.3 载荷对传动误差的影响
为了分析载荷对传动误差的影响规律,令模型中载荷T分别为200,300和400 N·m,轴承精度为6级,误差阶次为1阶,主动轮两轴承相位差为π/2,从动轮轴承相位差为0,分析结果如图11所示。
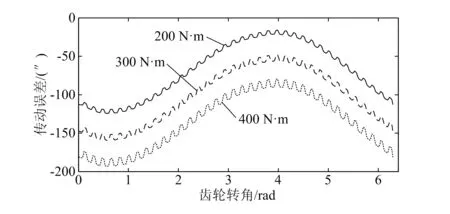
图11 载荷对传动误差的影响
由图11可知,载荷的增加不仅会使传动误差变大,还会使由啮合刚度导致的小波幅值变大,说明载荷的增加不仅会使轴承的变形增加,导致中心距变大,还会使齿轮的弹性变形增加。
4 结束语
本文建立了斜齿轮传动精度的分析模型,综合考虑了轴承的误差和弹性变形以及齿轮在轴系误差下的弹性变形与齿轮传动误差之间的关系,可为后续进行考虑轴承误差的齿轮动力学分析提供理论基础。算例分析表明,轴承的弹性变形与滚道圆度误差导致齿轮传动误差曲线呈现出大波的周期性波动的形式,与齿轮时变啮合刚度导致的小波周期误差相叠加形成齿轮传动综合误差,从而说明轴承的误差与弹性变形对齿轮传动精度影响较大。轴承精度的降低不影响齿轮传动误差曲线的大波的频率和相位,但是会增大大波的幅值。轴承误差相位的改变不仅影响传动误差大波的相位角,还会改变波动的幅值大小。载荷的增加不仅会导致传动误差变大,还会导致传动误差小波幅值的增加。

