例析四类“隐形圆”问题

叶 珊

福建省福安市第一中学 (355000)

近年来，随着对圆的方程加大的考查力度，许多“隐形圆”的问题不断呈现．所谓的“隐形圆”，就是在条件中没有直接给出有关圆的信息，而是隐藏在题目的信息中，要通过分析和转化，才能发现圆(或圆的方程)，从而可以利用圆的知识来解决问题．下面举例介绍四类常见类型，供参考．

一、隐含着圆的定义或圆的方程

例1 若圆C:(x-2a)2+(y-a-3)2=4上，总存在两个点到原点的距离为1，则实数a的取值范围是．

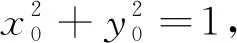
评注：从题设中找到了动点到定点的距离为定长，这就是圆的定义，抓住它建立圆的方程，从而再利用两圆相交的性质列出不等式求出参数范围就变得很容易了．

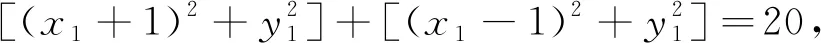
评注：依据题设中的平方和的条件得到了点A在一个已知圆上运动，再由给出的向量的线性关系，使问题转化D点在另一个已知圆上运动，如果点B固定，则就变成一个非常熟悉的问题了．

二、含有线段长的比式

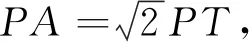
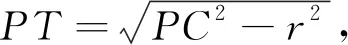
点评：这是一个“阿波罗斯尼圆”的问题，解题中抓住了给出的线段长等式，通过设动点，建立方程，然后再化简方程找到了一个隐含圆，这就将问题转化为直线与圆有交点问题了．

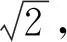
评注：要求直线PN的方程，由于N点坐标知道，则只需再求出点P坐标就行了，由给出的线段比可得点P在一个“阿波罗斯尼圆”上，又点P在直线PM上，将二者的方程求出，然后联立就能得到点P坐标，问题就能顺利解决了．

三、含有向量的模或数量积等式

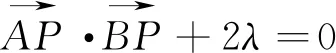
评注：本题中的解题核心，就是抓住所给的含向量数量积的等式，建立一个圆类方程，这为后续利用直线与圆相交解决问题提供了重要的支撑作用．

图1

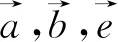
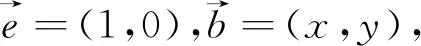
评注：题中没有点坐标，通过抓住单位向量设坐标，引出了直角坐标系，再设动点，根据已知条件得到动点的轨迹为圆，求出圆的方程后再运用圆心到直线的距离解决了问题，其中得到圆的方程并加以运用是解题核心．

四、挖掘四点共圆问题

例7 在平面直角坐标系xOy中，已知点

A(-4，0)，B(0，4)，从直线AB上一点P向圆x2+y2=4引两条切线PC,PD，切点分别为C,D.设线段CD的中点为N，求线段AN的长度的最大值．

图2

解析：如图2，AB所在的直线方程是x-y+4=0，设P(x0,y0)，则y0=x0+4①.

因为PC,PD是圆O的两条切线，所以P,C,O,D四点共圆，直径为PO，故此的圆的方程是x(x-x0)+y(y-y0)=0，即x2+y2-xx0-yy0=0，联立

评注：通过对已知的两个切线条件的分析，得到了P,C,O,D四点共圆，并求出了此圆的方程，这是问题解决的关键，而本题中运用了设而不求、整体求解的方法是解决圆的问题的常用求解方法．

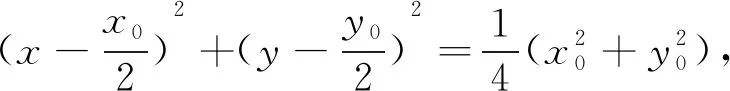
评注：抓住一个圆的两条切线是找到四点共圆的重要特征，还可以利用同弧(弦)所对的圆周角相等判断点共圆，在解题中灵活利用此类条件及时地求出圆的方程，然后再利用圆的方程解题，可降低难度，优化解题过程．

上面以例题说事，解析了四类常见问题，只是抛砖引玉而已，关于“隐形圆”问题比较多见，其中心思想是发现圆，然后再利用圆去解题，在平时的教学中，我们应该引导学生在这两个方面多下点功夫，会对学生以后应付各类考试有所帮助的．