构建同构式,化为单调性*
——从2020年山东卷21题的解法谈起
戚有建 李艳萍
江苏省扬州中学 (225009)
一、考题展示
题目(2020年新高考山东卷21题)已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求实数a的取值范围.

点评:本题是2020年新高考山东卷的第21题,是压轴、选拔题.第(1)问考查导数的几何意义,学生很容易上手;第(2)问考查用导数研究不等式恒成立问题,考查综合分析求解能力,分类讨论思想和等价转化思想有一定难度和区分度,本题结构简洁、表达流畅、静中有动、平中见奇、入口较宽,解法多样,有内涵、有思想、有新意,令人回味无穷,极具教学价值和研究价值,我们重点研究第(2)问.
二、常规解法

(1)当0 ①根据目前气袋制造工艺能力,气动闸最高挡水高度可达10m,宽度可达数百米,可以说在高水头大跨度可起伏的挡水设备方面,气动闸填补了国内空白。近期安装完成的贵阳南明河气动闸,挡水高度8m,跨度60m,是目前世界上挡水高度最高、跨度最长的同类闸坝。 另外,第(3)种情形a>1时也可以改进,通过放缩来处理会更简单,过程如下: 当a>1时,f(x)=aex-1-lnx+lna>ex-1-lnx,由第2种情形知ex-1-lnx≥1,∴符合要求. 构建同构不等式,借助单调性解题. 点评:解法2从题目的结构入手,构建同构不等式,借助单调性解题,是在是太简洁了,令人拍手叫好,其中改写成同构式的变形过程技巧性较强.变形过程中注意恒等式a=elna或a=ln(ea)的灵活运用,借助这两个恒等式,可以轻松实现指数化、对数化. 另外,要特别提出来的是构建同构式处理不等式实际上本质还是借助函数单调性来处理不等式,所以此种方法只能处理形如“f(x1)>f(x2)”结构的不等式. 分析:此类问题通常有两种处理方法:分离参数、构建差函数,但在本题中这两种通法都很困难,分参分不起来,若构建差函数则差函数的导数肯定会很繁杂,所以需要另辟蹊径.实际上,本题可以构建同构式,转化为单调性来处理,难点是如何改写成同构式. 分析:本题分离参数分不起来,若构建差函数则差函数的导数会很繁杂.实际上,本题可以构建同构式,转化为单调性来处理,难点是如何改写成同构式. 例3 若对任意x∈(1,+∞),不等式λeλx≥lnx恒成立,求实数λ的取值范围. 分析:本题的结构虽然看似简短,但是处理起来并不容易,分离参数分不起来,若构建差函数则差函数的导数也不简单.实际上,本题的结构中也蕴含着同构式,难点是如何变形改写成同构式.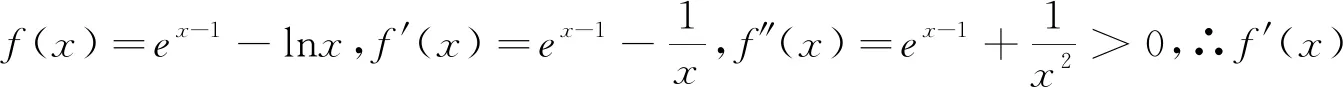




三、特殊解法

四、解法应用
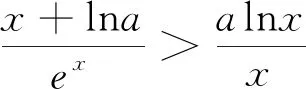

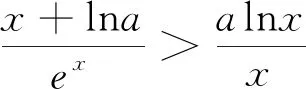


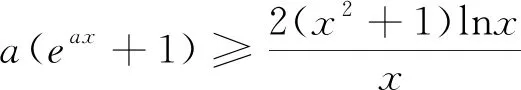
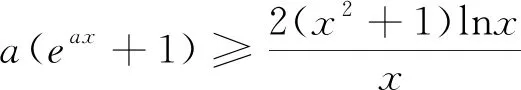

——以指数、对数函数同构问题为例

