用代换法证明若干新颖的不等式问题

邹守文

安徽省南陵县城东实验学校 (241300)

本文用代数代换法给出近期的一些国内外不等式题的统一证明，希望对读者有所启发.

例1 (加拿大数学杂志CRUX2020年2月号问题4451,GeorgeApostolopoulos供题)设a,b,c为正实数，证明：

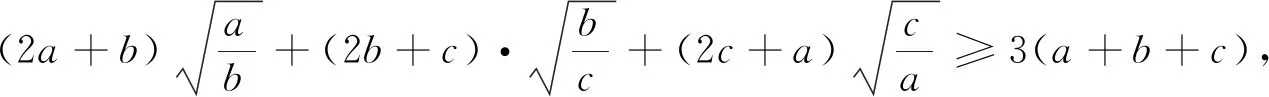
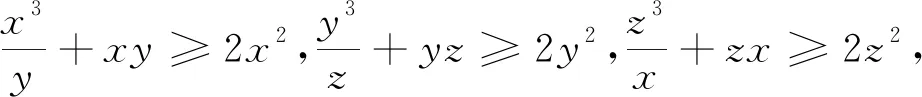
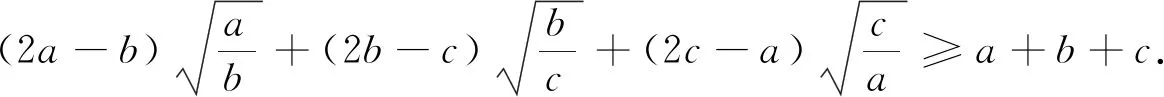
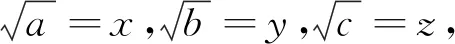
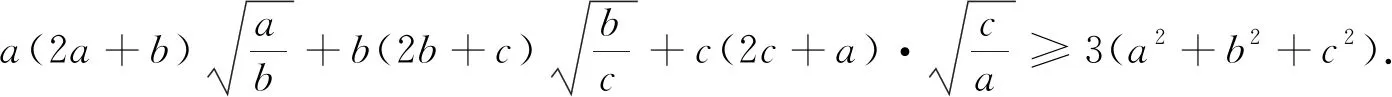
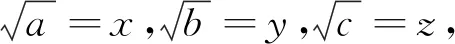
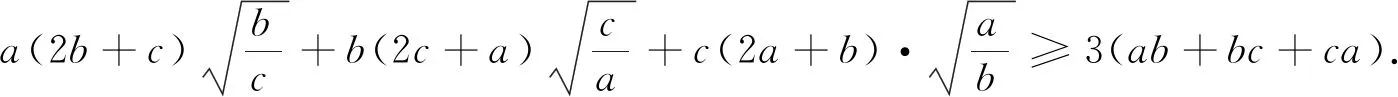
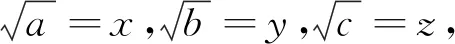
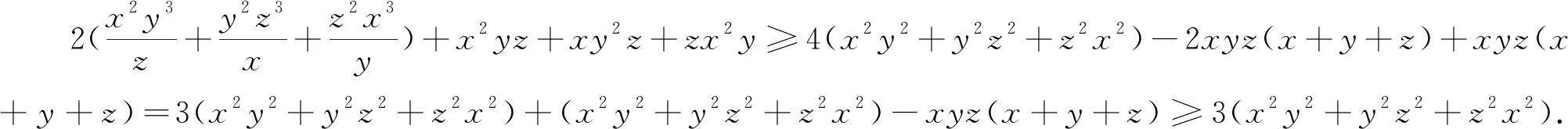
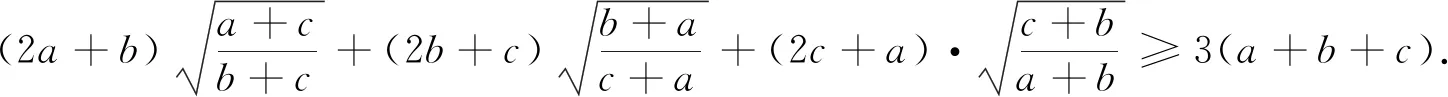
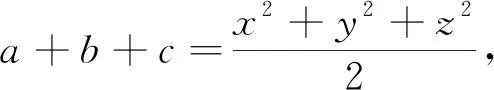
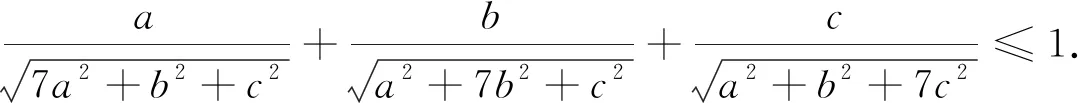
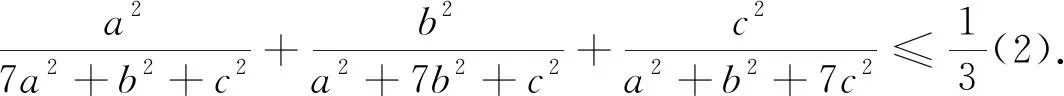
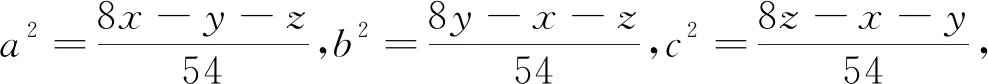
例7 (2020年3月15日不等式研究会中学群网友贵桂提出)已知正实数a,b,c满足abc=1，求证：a3+b3+c3+(ab)3+(bc)3+(ca)3≥2(a2b+b2c+c2a).

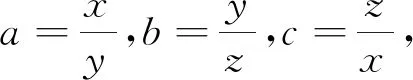
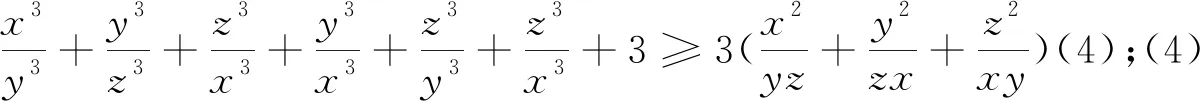
例8 (Leonard Giugiuc供题)已知a,b,c为满足abc=1的正实数，求证：(a+b+c)(ab+bc+ca)+3≥4(a+b+c)(6).

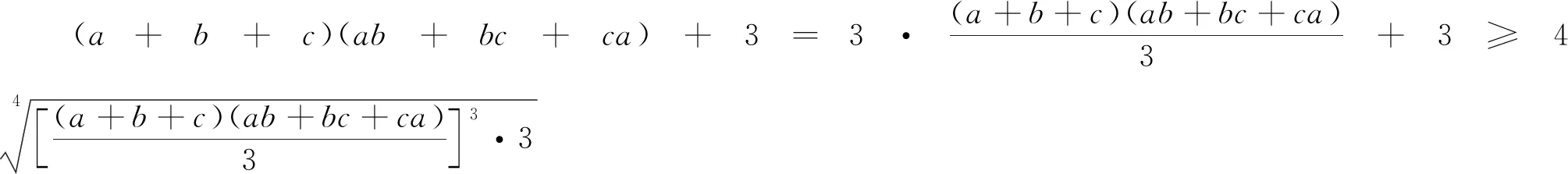
例9 (TituAndresscu供题Mathematica

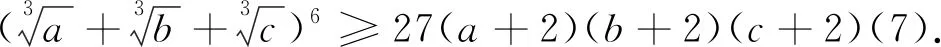
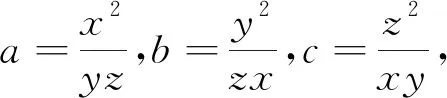
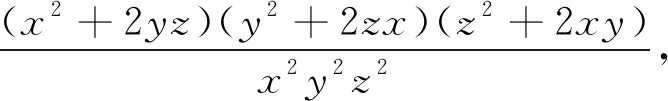
受褚先生思路的启发，给出下面的类似结论：

推论1 正实数a,b,c满足abc=1.求证3(a+b+c)2≥(a+2)(b+2)(c+2)(8).

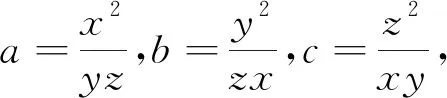
推论2 正实数a,b,c满足abc=1.求证9(a2+b2+c2)≥(a+2)(b+2)(c+2)(9).

证明：因为9(a2+b2+c2)≥3(a+b+c)2，结合(7)式即知式(9)成立.

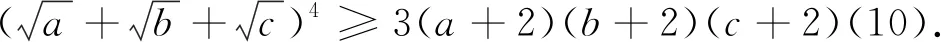
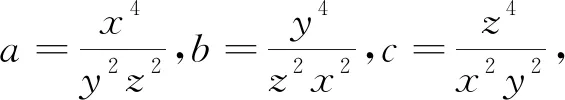
致谢：本文在写作过程中得到文武光华数学工作室褚小光先生的大力帮助，谨表谢意！