基于运算素养探寻一道高考真题的源与流*

洪丽敏

福建省南安第一中学 (362300)

数学运算作为数学六大核心素养之一，是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，它不仅是现代人赖以生存的必备素质之一，也影响着其他素养的培养.在普通高中课程标准(2017年版)中，每个主题的学业要求重点必定包含培养或提高数学运算素养.

在高中数学核心素养培养过程中，教材是最基本、最重要的载体，课堂教学是训练场，高考则是主战场．近年来，高考命题已从基于“能力”到基于“素养”考试评价的转变，逐步树立“以素养立意命题”的指导思想，注重考查学生的核心素养.比如2019年全国卷Ⅰ做了较大形式的调整，导致相当一部分考生不适应，但却很好的传递了一个信息——不可忽视教材和运算素养的培养.且不说网红考题“断臂维纳斯”问题其实就在初中9年级上册“平行线分线段成比例”的阅读材料“黄金分割”，单说其理20题，就是教材两道习题基于运算的组装.

下面，笔者以2019年全国Ⅰ卷理20题为例，基于运算素养下，谈谈该高考试题的源与流，意在抛砖引玉.

1.高考真题展示

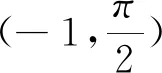
本题用证明的形式探求函数的零点问题，形式新颖，却容易造成多数考生的不适应，其原因主要有：一不适应：虽是研究零点问题，但却不是常见的“已知零点个数，逆向求参”问题；二不适应：函数f(x)的形式在全国Ⅰ卷不多见，容易蒙圈；三不适应：因题序改变，以往导数题都为21题，多数学生对(2)问本持着“放弃”的想法，如今虽调整为20题，但因没有心理准备，学生容易缺乏继续求解的欲望.以上种种原因导致本题得分率低下.

2.源之探——饮水思源

本题真的如考生所反应的那样难吗？其实不然！

让我们先回顾一下人教A版选修2-2:第32页B组第一题：

利用函数的单调性，证明下列不等式，并通过函数的图象直观验证：

(1)sinx0,x∈(0，1).(3)ex>1+x,x≠0；(4)lnx0．

由(3)我们知道由ex>1+x,x≠0可得到ex≥x+1(x∈R)，两边取对数x≥ln(x+1)(x>-1)，如图1；由(1)可知sinxx,x∈(-π，0),进而可得y=x与y=sinx在R上有且只有一个交点，如图2；

把两张图整到同一坐标系，如图3；再去掉直线y=x，如图4.

此时我们不难发现，这个问题就是2019年全国卷Ⅰ理20题的第(2)问了.我们无法得知高考命题者是如何命制本试题的，但我们却清楚试题的题源，那就是人手一册的教材！

可见，无论是基础年级的教学，或是高三年的全面复习，在培养考生数学核心素养的过程中，教材是最基本、最重要的载体，教师要注重引导学生重视教材，切不可盲目涮题，陷于“题海”而不能自拔.

3.流之拓——源远流长

3.1 流之拓1——解题策略

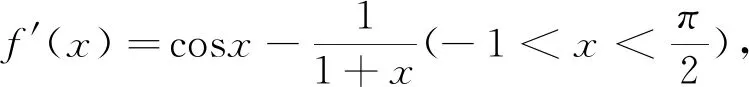
(2)略.

评析：本题(1)、(2)的解题思路类似，且对广大师生而言并不陌生，它们都是零点问题，都离不开“零点存在定理”和“设而不求思想”，而这两者在高考试题中屡见不鲜，如2012年全国卷Ⅰ文21题、2013年全国卷Ⅱ理21题、2015年全国卷Ⅱ理21题、2015年全国卷Ⅰ文21题、2016年全国卷Ⅱ理21题文20题、2019年全国卷Ⅰ文20题、理20题、2019年全国卷Ⅱ文21题、理20题.可见，零点问题是利用导数解决问题的重要内容，应引起广大师生足够的重视.

3.2 流之拓2——题源再探

从上，我们看到本题的题源之一为ex>1+x,x≠0，这是一个值得深究的问题，以该题为背景的题目比比皆是，这里不一一赘述.

教学中，我们可以引导学生往两条线展开思考与探究：

一是代数运算方面——数学运算素养.

探究1 由ex≥x+1(x∈R)到x≥ln(x+1)(x>-1)，其实就是常见的“指对数互化运算”，借助“指对数互化运算”实现ex,x,lnx，…之间的转化，在各地省市质检，乃至高考命题中都屡见不鲜.比如

(2013年全国卷Ⅱ理21)已知函数f(x)=ex-ln(x+m)．

(Ⅰ)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；(Ⅱ)当m≤2时，证明f(x)>0．

略解：(Ⅰ)略．(Ⅱ)当m≤2时，x∈(-m,+∞)时，ln(x+m)≤ln(x+2)，则要证明f(x)>0，只需证明当m=2时f(x)>0(加强不等式思想)．即证：f(x)=ex-ln(x+2)>0．

别证：①当-20成立；

②易证当x>-1时有ex≥1+x(当且仅当x=0时等号成立，过程略)，则有x≥ln(x+1)，则有x+1>ln(x+2)(当且仅当x=-1时等号成立)，即当x>-1时，有f(x)=ex-ln(x+2)≥(1+x)-ln(x+2)>0成立．

综上，当m≤2时，f(x)>0成立．

探究2 加减乘除四则运算可以使数学运算更为丰满，构造更多的函数模型.

比如由ex>1+x,x≠0可得到：①ex≥x+1，进而替换得到②ex-1≥x，两边取对数得③x-1≥lnx(x>0)，移项可得到④x≥lnx+1=ln(ex)，再取指数可得到⑤ex≥ex，…

二是借助图象直观呈现——直观想象素养.

把探究2中5个问题用图形表示，依次为以下图5-图9.

最后提炼本质——数学抽象：以上问题的本质都是研究切线问题，都可借助导数加以研究，这里就不一一探究.

面对精彩纷呈的试题，“问渠哪得清如许，为有源头活水来”，源头就是教材．数学教材为“教”与“学”活动提供学习主题、基本线索和具体内容，是发展学生数学学科核心素养的重要教学资源，也是高考命题的一个重要取材渠道.

值得一提的是，立足数学运算，对教材的进行开发性研究，是一种普遍适用的研究方法，也是教师教学能力自我提升的一种有效手段.教师必须在重视课本的钻研和探究的同时加强对学生运算能力的培养，这样，数学教学方可“源远流长”、创新发展．