基于MATLAB对球谐函数及其原子轨道的可视化研究

郑兴荣，杨 伟，张馨丹，杜晨敏，李小龙，唐 歡

(陇东学院电气工程学院物理系，庆阳 745000)

1 引 言

量子力学是描述微观世界，研究微观粒子运动规律以及相关特性的一门理论和学科[1-4]，与相对论一起被认为是现代物理学的两大支柱，且这两门学科是许多理论和学科的基础，尤其是近几十年出现的新学科，如物理学中的群论、核结构、电子结构理论、强子物理和粒子物理学、计算物理学、固体物理学、原子物理学、量子化学、分子生物学、拓扑学等[5-12]. 在许多现代技术装备中，量子力学及其相关特性的效应起了重要的作用. 从激光、电子显微镜、原子钟到核磁共振的医学图像显示装置，都关键地依靠了量子力学的原理和效应. 根据量子理论，粒子的行为常常像波，用于描述粒子行为的“波函数”预测一个粒子可能的特性.近年来，随着计算机技术的高速发展，计算机三维重构技术日趋成熟，结合计算物理方法和MATLAB软件的强大功能使得抽象量子理论的可视化分析更加形象、逼真[13-16]. 基于MATLAB软件的可视化研究不仅运用在理论和实验教学方面[17-19]，而且在科学研究上的发展更为迅速[20-24]. 因此，微观、抽象粒子的可视化被众多研究者进行了大量的研究，尤其是近十几年已趋于白热化[20，25-26]. 本文根据量子力学中角动量算符和连带勒让德方程[27-30]，在设定广义函数的条件下利用微积分下的分离变量法推出球谐函数的一般方程式[31]，把不同的角量子数和磁量子数代入通项中，进而得出不同的角量子数和磁量子下的球谐函数[32-34]. 而不同的角量子数对应不同的s，p，d，f…状态，因此利用MATLAB软件强大的作图功能，对不同的n、l所对应的球谐函数以及不同的n、l所对应的原子轨道进行仿真模拟，其可视化的结果对研究球谐函数及其原子轨道提供了一条便利的途径.

本文利用MATLAB仿真模拟功能得到可视化的结果，这种可视化结果可以直观地、详细地、具体地观测到球谐函数及其原子轨道的运动特性，将一个抽象的、难懂的问题具体化和简易化. 本课题的前期工作已经将n维线性谐振子、氢原子进行了可视化研究，结合本课题的研究结果，已经证明了对抽象的量子理论进行可视化研究是一种新的研究思路，它既可以当做实验来验证理论，也可以作为理论指导实验. 因此，本文的这种创新具有很大的科学研究潜力、市场价值和应用价值.

2 球谐函数的理论模型与推导

2.1 角动量算符

(1)

因此，有

(2)

为了讨论角动量算符的本征值方程，接下来本文把这些算符用球坐标来表示.令

x=rsinθcosφ，y=rsinθsinφ，z=rcosθ

(3)

其中φ∈[0，2π]，θ∈[0，π].利用几何知识，对r2=x2+y2+z2两边的x，y，z求偏导数，得

(4)

同理，对cosθ=z/r两边的x，y，z求偏导数，有

(5)

对tanφ=y/x两边的x，y，z求偏导数，有

(6)

利用“链式法则”求偏微分，则有

(7)

(8)

所以

(9)

2.2 球谐函数

由上式可知，这些角动量算符与径向坐标r无关，只与角度θ和φ有关，所以角动量算符平方的本征值方程为

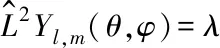
(10)

即

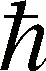
(11)

在保证函数Yl,m(θ,φ)为有限的条件下，利用分离变量法Y(θ,φ)=Θ(θ)Φ(φ)可求得该二阶偏微分方程. 即

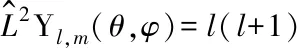
(12)

则角动量平方算符的本征值为

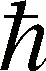
(13)

其中l=0,1,2,3,…称为角量子数.

利用缔合勒让德方程，归一化性质等，得到角动量平方算符的本征函数为

(14)

(15)

球谐函数是角动量和z分量的共同本征函数，全部的球谐函数构成一个正交归一的完备集合，即

(16)

3 仿真结果与讨论

3.1 利用MATLAB对球谐函数进行仿真

根据前面球谐函数的理论推导，针对不同的轨道量子数l和磁量子数m，利用MATLAB进行编程，得到了21组不同的球谐函数图像，如图1所示.通过对球谐函数可视化的研究，将抽象化转变为具体化，加深了对球谐函数的理解.

由图1可以看出，当l=m=0时，球谐函数的可视化图形是一个均匀的球体；当l=m≠0时，图形是由2l或者2m个椭球水平叠加而成；当m=1时，对于不同的l值，图形是由2n(n=1,2,3…)个椭球上下叠加而成；当n=3且l>n时，图形由6(n-2)个椭球上下叠加而成.例如，当l=m=0时，是一个均匀的球体；当l=1，m=1时，是两个均匀球在水平方向上叠加在一起构成的；当l=2，m=0时，是两个球和一个圆饼状在竖直方向上叠加在一起构成的；而当l=2，m=1时，是四个椭球在竖直方向上叠加在一起构成的；当l=2，m=2时，是四个椭球在水平方向上叠加在一起构成的；当l=3，m=0时，是由两个球和两个圆饼状叠加在一起构成；当l=3，m=1时，由四个椭球和两个圆饼状叠加在一起构成；当l=3，m=2时，由八个椭球上下叠加在一起构成；当l=3，m=3时，由六个椭球叠加在一起构成；当l=4，m=4时，由八个椭球叠加在一起构成；当l=4，m=3时，由上下各为六个椭球叠加在一起构成的；当l=5，m=1时，由上部两个椭球中间六个椭球下部两个椭球叠加在一起构成的.

这种可视化的结果为研究球谐函数的其他特性提供了一种更为简明扼要、直观清晰的途径.

3.2 球谐函数的原子轨道的仿真模拟

原子轨道在微观粒子、结构化学中的应用非常广泛，是微观结构和量子化学研究中的重要内容.球谐函数原子轨道图形种类繁多、形态复杂，不易理解.基于此，本文利用前面的理论推导，结合MATLAB的作图功能，对球谐函数的原子轨道进行了三维和彩色平面等值线图仿真模拟，如图2所示.球谐函数原子轨道中不同的角量子数对应不同的状态，l为0，1，2，3…，分别对应的状态为s，p，d，f….

图1 球谐函数的仿真模拟图Fig.1 Simulation diagrams of the spherical harmonic functions

由图2可以看出,仿真模拟出的可视化图形可以直观地观测到原子轨道的运动情况，不同的颜色代表原子轨道的运动出现在空间的不同位置,在原子运动过程中存在极值，通过仿真图的颜色深浅可以直观地得出极值所在区域.

这种对三维立体和彩色平面等值线进行的可视化图形，可以加深对原子轨道运动情况的理解，为微观结构的研究提供了更为简单、可操作性强的方法.

利用MATLAB的仿真功能，对原子轨道所对应的径向波函数绘制二维平面曲线图，见图3.

由图3可以看出，当r发生变化时，径向分布几率密度也随之发生改变.当主量子数n越大时，原子轨道的最可几径向距离越大，则原子轨道的扩散程度越大；对单原子而言，当主量子数n相同时，角量子数l对原子轨道的径向分布影响不大，仅随角量子数l的增大，最可几径向距离稍有减小.

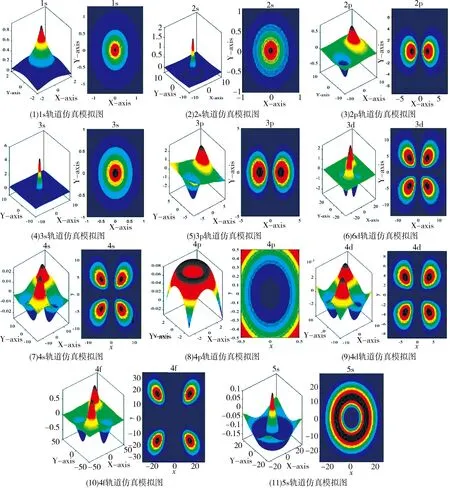
图2 球谐函数原子轨道的仿真模拟图Fig.2 Simulation diagrams of the atomic orbitals of spherical harmonic function

4 结 论

球谐函数作为现代物理学中的一类特殊函数，是拉普拉斯方程的球坐标系形式解的角度部分，在经典场论、量子力学等领域广泛应用，解决了物理学中的许多问题.本文基于量子力学中的角动量算符和连带勒让德方程，设定广义函数的条件下，利用分离变量法推导出球谐函数的一般方程式，进而解出n、l分别为0，1，2，3，4，5时的球谐函数.另外，根据球坐标的自变量定义域，设定自变量θ、φ的条件下，得到了不同状态的球谐函数及其原子轨道，并对其进行了可视化研究.最后，利用 MATLAB软件对不同的n、l所对应的球谐函数和原子轨道进行仿真模拟，得到了简明扼要、直观清晰的可视化结果.这种可视化的研究思路为研究球谐函数及其原子轨道的其他特性提供了一条便利的途径.通过以上研究表明，MATLAB是解决微观结构数值计算和可视化问题的一种更为形象、直观的工具，有广泛的适用性.利用MATLAB软件对球谐函数及其原子轨道进行了可视化分析，可以形象地认识微观粒子的运动形态和量子理论抽象的波函数概念.