基于舰载主动声纳的水下目标距离精确测量方法

王海川

（江苏自动化研究所，江苏 连云港 222061）

0 引言

国外鱼雷装备技术和性能的不断发展和提升，对水面舰艇造成的水下威胁日益增大。目前水面舰艇对鱼雷的近程防御主要依赖声诱饵、声干扰器等软对抗武器［1］，在舰艇近程范围内缺乏有效的硬杀伤手段［2］。随着超空泡射弹和高频主动声纳技术的日益成熟，舰炮发射超空泡射弹在末端拦截水下来袭鱼雷成为可能，由此促进了舰载超空泡射弹末端反鱼雷武器系统的快速发展［3］。

要使用舰载小口径舰炮发射超空泡射弹，采用直接命中体制有效拦截鱼雷、UUV 等水下运动小目标，就必须要提高高频主动声纳对目标距离和方位角、深度的测量和处理精度［4］。由于声波在海水中的传播速度通常为1 500 m/s 左右，远小于电磁波在空气中的传播速度，因此，舰载主动声纳对水中目标距离的测量特性与舰载雷达对空中目标距离测量特性有着较大的不同。

舰载雷达在对空中目标测距时，由于电磁波在空气中的传播速度为3×108m/s，电磁波从发射到接收到反射回波的时间非常短，即使是对150 km 远的目标，电磁波传播往返的时间也只有1 ms，在此时间里由于舰艇运动所导致的雷达位置变化值一般不会超过2 cm，这与雷达的距离测量误差通常为几米相比，可以忽略不计；因此，舰载雷达的距离测量可以直接使用从电磁波发射到目标发射回波到达的时间乘以电磁波在空气中的传播速度再除以2得到。

主动声纳对水中目标测距时，从声纳发射声波到接收到目标回波需要较长的时间，而在这段时间里舰艇的位置会发生较大的变化，例如对距离为300 m 的水中目标测距时，声波传播的往返时间为0.4 s，在此段时间里舰艇假使按20 kn 的航速运动，将会带来4.1 m 的声纳位置变化，因此，如果按照传统的声纳脉冲测距方法，将声波传播的往返时间乘以声波传播速度再除以2 作为目标测量距离［5］，就会带来较大的距离测量原理误差，因此，必须针对主动声纳的测距特性研究目标距离的精确求取方法。

本文主要针对舰载主动声纳目标测距特性，研究在舰艇航行运动情况下目标距离精确测量原理，提出基于主动声纳的目标距离计算模型，为该方法在装备中的应用提供技术支撑。

1 基于舰载主动声纳的目标距离精确测量原理

由于声波在海水中的传播速度为1 500 m/s 左右，舰载主动声纳在对水下运动目标进行探测和跟踪的过程中，所发射声波的往返传播需要一定的时间，而在这段时间内，目标和本舰的位置都将发生变化，因此，必须结合主动声纳的目标距离测量特性研究声纳测距原理。基于主动声纳的目标距离精确测量原理示意图如图1 所示。

如图1 所示，舰载主动声纳安装在舰艇前方的球鼻艏内，舰艇航行到A 点时主动声纳发射声波，此时水下目标在E 点位置；当声波与水下目标在O点相遇时，舰艇到达B 点；当水下目标反射的声波回到舰艇被声纳接收到时，舰艇航行到C 点，水下目标航行到F 点，其中D 点是从O 点向AC 延长线连接垂直线的交点。由于在舰艇航行到C 点时，主动声纳才接收到目标回波信号，尽管此时水下目标已航行到F 点，但实质上声纳测量到的是水下目标航行到O 点时相对于舰艇在C 点的相对位置信息，而不是目标现在点F 的相对位置信息。主动声纳根据接收到的目标回波信号，通过信号处理可以测量出声波信号往返时间ΔT（由此可以计算出声波信号往返行程D0+D）和目标舷角qw，以及目标高低角ε数值信息（三维主动声纳），为了支持对水下目标运动参数的滤波解算，将需要计算求取与目标舷角qw和高低角ε 测量值严格对应的目标距离D，即线段OC 的长度。

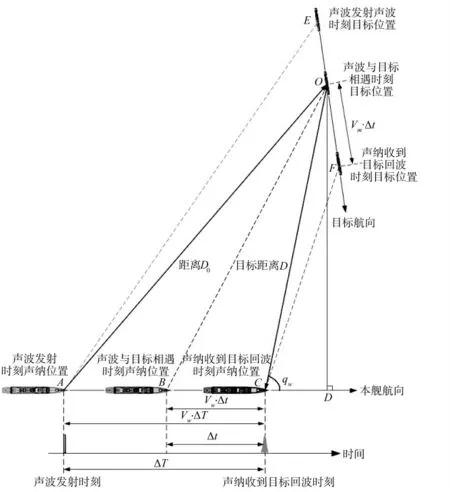
图1 基于主动声纳的目标距离精确测量原理示意图

为推导基于主动声纳的目标距离精确计算模型，可以假定在声波往返传播的短暂时间内（目标距离为1 km 时声波往返传播的时间仅为1.3 s），本舰为匀速直线运动；在水下目标深度不大和距离仅几百米的情况下，可以假定声波的往返传播行程近似为直线；另外为模型推导表述方便，设定：

●Cs为声波在海水中的传播速度，取1 500 m/s；

●ΔT 为声波往返传播时间（从声纳发射至接收到目标回波的时间间隔，由声纳测量获取）；

●Δt 为声波反射段传播时间（从水下目标反射声波时刻开始，到目标回波到达的时间间隔）；

●D0为声波与目标相遇时目标位置与声波发射时刻声纳位置之间的斜距离；

●D 为目标距离（声波被目标反射位置与目标回波到达时声纳位置之间的斜距离）；

●qw为目标舷角（由主动声纳测量获取）；

●ε 为目标俯仰角（由三维主动声纳测量获取）；

●Vw为本舰航速（由舰艇导航系统的计程仪提供）。

由图1 可以看出：

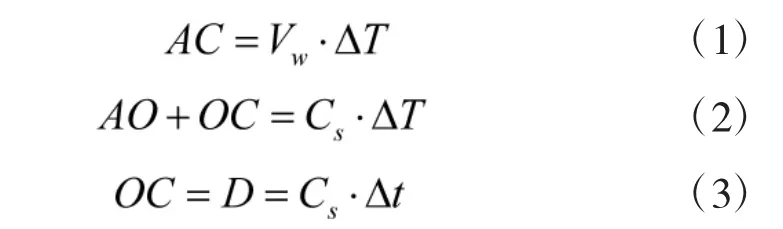
由式（2）可以求得：

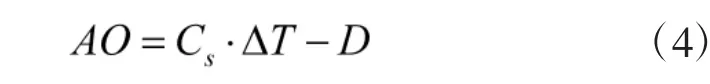
在直角△OCD 中：

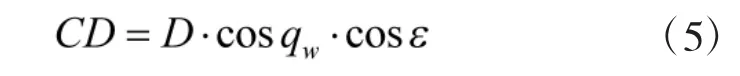
根据勾股定理：

可以求得：

在直角△OAD 中，考虑目标舷角大于或小于等于90°的情况，根据勾股定理：

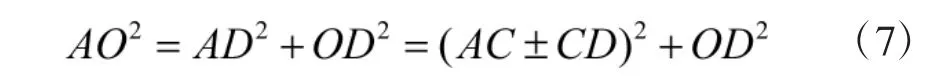
将式（1）、式（4）～式（6）带入式（7）可得：

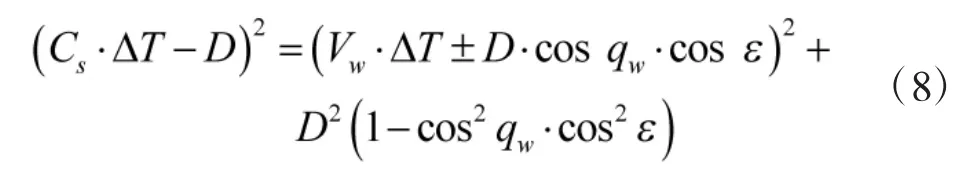
将式（8）展开合并后可求得目标距离精确计算模型：

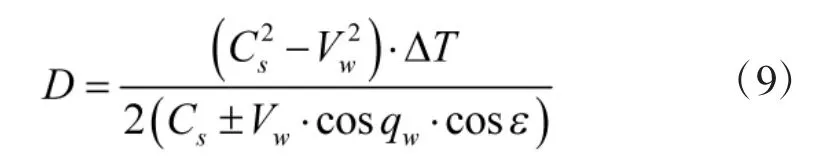
当目标舷角绝对值小于等于90°时：

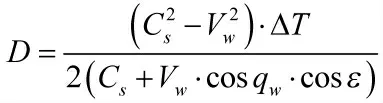
当目标舷角绝对值大于90°时：

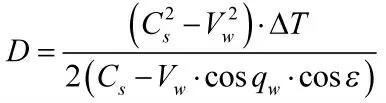
再由式（3）、式（9）可以求得：

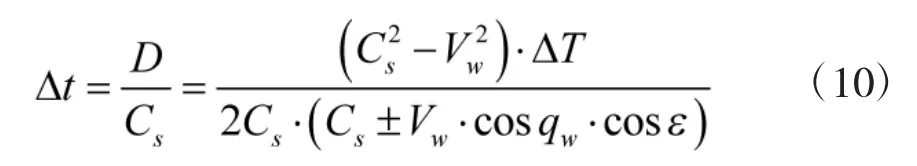
同样当目标舷角绝对值小于等于90°时：

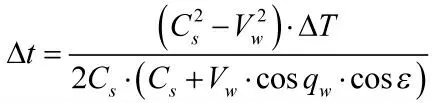
当目标舷角绝对值大于90°时：

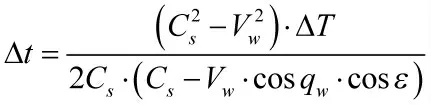
由式（10）所求取的相对于目标回波到达时刻的声波反射段传播时间Δt，可用于从声纳测量时刻（声波与目标相遇时刻）的目标位置，精确外推计算目标当前时刻位置。

2 工程简化计算模型

在本舰静止的情况下，Vw=0，则式（9）、式（10）可变化为：

式（11）即为传统的声纳脉冲测距计算公式［5］。可见传统的声纳脉冲测距方法，忽略了本舰运动对声纳位置变化的影响因素。

由于声波在海水中的传播速度Cs为1 500 m/s左右，而水面舰艇的航行速度Vw通常不大于30 kn（约15.4 m/s），Cs2远大于Vw2，因此，在工程应用中，式（9）、式（10）可简化为：

另外，高频主动声纳通常安装在舰艇前部水下球鼻艏内，水下鱼雷在末端攻击段的航行深度通常为8 m～20 m，那么声纳在500 m～100 m 距离范围内测量的目标高低角的范围约为2°～10°。在工程应用中，当目标高低角的变化范围较小，对目标距离测量精度的影响较弱的情况下，可将式（13）、式（14）去掉目标高低角项，进一步简化为：

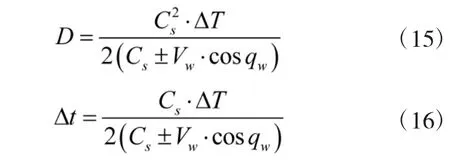
式（15）、式（16）即为改进后的目标距离和声波反射传播时间工程简化计算模型。

3 目标距离测量精度影响因素分析

由式（9）可以看出，影响目标距离测量精度的主要因素有：

1）声波在水中的传播速度Cs。在海水中影响声波传播速度的主要因素有：海水盐度、温度和压力（深度）。当温度为10℃、深度为0 m、盐度为35 ppt时，声速为1 490 m/s，以此“标准”声速为基础，存在几个声速增量的近似系数：海水温度每增加1℃，声速增加3.4 m/s；海水盐度每增加1 ppt，声速增加1.2 m/s；深度每增加100 m，声速增加1.7 m/s［6］。可见在深度变化不大的情况下，温度是影响声波在水中传播速度的重要因素。通过声纳距离标校和水文测量信息的应用，可对声波传播速度进行修正［7］，以保证声纳的测距精度。在目标距离为300 m 时，声波速度偏差5 m/s 所带来的距离误差约为1.0 m。

2）经目标发射的声波往返时间间隔ΔT。主动声纳的脉冲计时误差经距离校准后通常可做到小于2 ms。在声波传播速度为1 500 m/s 的情况下，声纳脉冲计时误差为2 ms 所导致的距离误差约1.5 m。

以上两项影响因素，在传统的声纳脉冲测距方法中同样存在，在工程应用中可以采用距离标校修正等方法减小其影响。本文主要考虑下述3 项因素的影响。

3）本舰航速Vw。舰艇航速通常由导航系统中的计程仪测量获取，舰载计程仪对舰艇航速的测量误差（RMS）通常可做到小于0.5 kn。在本舰航速24 kn、目标距离为500 m、深度为20 m、目标舷角为0°的情况下，本舰航速测量误差为0.5 kn 时所带来的距离误差为0.15 m。

4）声纳测量的目标舷角qw。高频主动声纳对近程目标的测向精度（RMS）通常可做到1°左右。在本舰航速24 kn、目标距离为500 m、深度为20 m、目标舷角为0°的情况下，目标舷角误差为3°所带来的距离误差仅有0.01 m。

5）声纳测量的目标俯仰角ε。三维声纳可实现对目标俯仰角的测量，高频声纳对近距离目标俯仰角的测量精度（RMS）也可做到1°左右。在本舰航速24 kn、目标距离为500 m、深度为20 m、目标舷角为0°的情况下，目标俯仰角误差为3°所带来的距离误差仅有0.02 m。

通过对上述后3 项影响因素的分析计算来看，本舰航速测量误差是影响目标距离测量精度的主要因素，但处于可接受范围内；声纳对目标舷角和俯仰角的测量误差对测距精度造成的影响很小，因此，本文所提出的目标距离精确计算模型具有很好的工程应用价值。

4 不同计算模型的计算误差对比分析

4.1 传统模型相比精确计算模型的计算误差对比分析

为对比分析传统模型相比精确计算模型的计算误差，首先设定本舰航速为24 kn、目标相对声纳的深度为20 m，由此计算出对应不同距离和不同目标舷角情况下，传统距离计算模型相比精确距离计算模型的计算误差，如图2 所示。

由图2 可以看出，在目标舷角为0°和180°时，传统距离计算模型的距离和时间计算误差最大，在目标舷角为±90°时，传统距离计算模型的距离和时间计算误差最小；另外随着目标距离增大，二项误差也都随之增大。在目标舷角为30°、目标距离为400 m 时，传统模型的目标距离计算误差为5.5 m，声波反射段传播时间计算误差为3.7 ms。

图2 不同目标舷角不同距离情况下传统模型相比精确计算模型的计算误差对比图

其次，设定目标相对声纳传感器的深度为20 m，目标舷角为0°，由此计算出对应不同距离和不同舰艇航速情况下，传统距离计算模型相比精确距离计算模型的计算误差，如图3 所示。

由图3 可以看出，随着本舰航速和目标距离的增大，传统距离计算模型相比精确距离计算模型的目标距离和声波反射段传播时间的计算误差都随之增大。在本舰航速为24 kn、目标距离为500 m 时，传统模型的距离计算误差为8 m，声波反射段传播时间计算误差为5.3 ms。

图3 不同舰艇航速不同距离情况下传统模型相比精确计算模型的计算误差对比图

最后，设定本舰航速为24 kn、目标舷角为0°，由此计算出对应不同距离和不同目标俯仰角情况下，传统距离计算模型相比精确距离计算模型的计算误差，如图4 所示。

由图4 可以看出，在相同距离、本舰航速和目标舷角的条件下，目标俯仰角的变化影响相对较小。在目标俯仰角从-20°到0°变化的情况下，在目标距离500 m 范围内传统模型距离计算误差小于0.3 m，声波反射段传播时间计算误差不超过0.4 ms。

图4 不同目标俯仰角不同距离情况下传统模型相比精确计算模型的计算误差对比图

通过上述计算分析可以看出，传统计算模型相比精确距离计算模型，在目标处于舰艇艏艉方向附近和舰艇航行的情况下，具有较大的原理计算误差。在本舰航速为24 kn、目标舷角为0°、目标距离为500 m 时，传统模型的距离计算误差达到8 m，因此，改进后的精确距离计算模型可显著提高距离测量精度。

4.2 工程简化模型相比精确计算模型的计算误差对比分析

为进一步分析对比工程简化计算模型相比精确距离计算模型的计算误差，也首先设定本舰航速为24 kn、目标相对声纳的深度为20 m，由此计算出对应不同距离和不同目标舷角情况下，工程简化计算模型相比精确距离计算模型的计算误差，如图5所示。

图5 不同目标舷角不同距离情况下工程简化模型相比精确计算模型的计算误差对比图

由图5 可以看出，工程简化计算模型相比精确距离计算模型的计算误差很小，在目标距离500 m范围内工程简化模型的目标距离计算误差不超过0.13 m，声波反射段传播时间计算误差不超过0.14 ms。

其次，设定目标相对声纳传感器的深度为20 m，目标舷角为0°，由此计算出对应不同距离和不同本舰航速情况下，工程简化计算模型相比精确距离计算模型的计算误差，如图6 所示。

由图6 可以看出，虽然随着本舰航速和目标距离的增大，计算误差单调增大，但是，在目标距离500 m 范围内，工程简化计算模型相比精确距离计算模型的目标距离计算误差不超过0.2 m，声波反射段传播时间计算误差不超过0.13 ms。

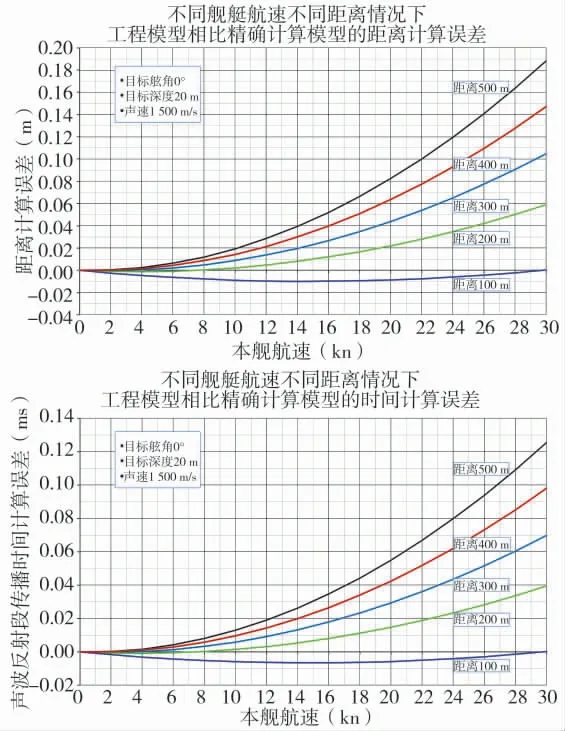
图6 不同舰艇航速不同距离情况下工程简化模型相比精确计算模型的计算误差对比图

通过上述计算分析可以看出，工程简化计算模型相比精确距离计算模型的计算误差较小，与声纳的距离测量误差相差一个数量级，因此，工程简化计算模型具有很好的工程应用价值。此外，工程简化计算模型对仅能测量距离和方位角的二维主动声纳，更具有工程应用价值。

5 结论

在水面舰艇近程水下防御系统中，提高主动声纳对近程来袭鱼雷、UUV 等水下运动目标的距离测量精度，有利于提高火控滤波解算精度，从而有利于提高超空泡射弹对来袭鱼雷、UUV 等水下小目标的命中概率。本文针对舰载主动声纳对水中目标的测距特性，研究舰艇航行运动情况下主动声纳对水中近程目标的距离测量原理，提出基于主动声纳的目标距离精确计算模型，并在对目标距离测量精度影响因素分析的基础上，提出了适合工程应用的改进计算模型。计算对比结果表明，该改进计算模型可有效提高舰载主动声纳对水中目标距离的测量精度。该方法可为主动声纳测距方法的改进提供技术参考。