变桨距四旋翼无人飞行器航迹跟踪控制

王 振，刘苹妮，马国亮

（空军工程大学空管领航学院，西安 710051）

0 引言

对定桨距小型四旋翼飞行器的研究已经有十几年的历史。加拿大的A Tayebi 和S McGilvary 证明了使用四旋翼设计可以实现稳定飞行［1］。澳大利亚的Phillip McKerrow 对其进行了精确的建模［2］。国内学者对定桨距四旋翼飞行器的研究集中在飞行器控制算法方面［3-4］。然而，定桨距四旋翼飞行器由于定桨距机构的限制，导致其只能通过改变直流电机的转速来改变旋翼产生的升力，并且只能产生方向向上的升力。同时，由于电机存在转动惯量，改变直流电机两端的电压，若要得到期望的转速则需要较长时间。因此，定桨距机构的限制将限制四旋翼飞行器的机动性能。

变桨距技术通过控制桨叶自动旋转到主控制器设定的角度，使叶片的迎风角始终保持在最佳位置，从而获得更好的空气动力学性能［1-2］。变桨距调节技术分为同步变桨距调节技术和独立变桨距调节技术［3-4］，已被广泛应用于风力［5-6］、潮流［7］发电机组。将变桨距技术应用于微小型四旋翼飞行器控制系统，可极大地减小飞行器的控制延迟，提高姿态响应，增加飞行器的机动性和灵活性，因此，变桨距四旋翼飞行器控制技术逐渐成为研究热点［8-11］。

针对四旋翼飞行器系统多变量、欠驱动、强耦合以及干扰敏感等特性［12］，本文在电机旋翼系统动力学模型的基础上，推导变桨距电机旋翼系统控制律，基于牛顿-欧拉方程和四元数运动学，建立四旋翼飞行器动力学模型，推导桨距角分配矩阵，设计航迹跟踪控制律，实现对变桨距四旋翼飞行器的高精度航迹跟踪控制。

1 变桨距电机旋翼系统控制模型

1.1 电机旋翼系统动力学模型

四旋翼飞行器采用无刷直流电机作为驱动器来控制螺旋桨的转速ω：

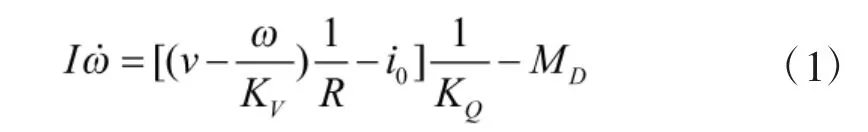
式中，v 为电机的终端电压，KV为电机电压常数，R为电机转子的总阻抗，i0为空转电流，KQ为电机转矩常数，MD为电机的阻力矩。

根据叶素理论和动量理论，旋翼转动产生的升力和阻力矩分别为：

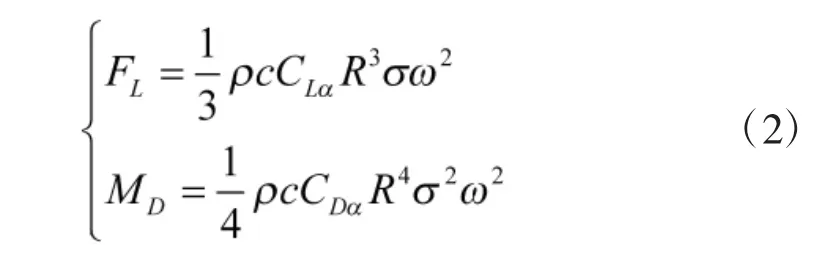
式中，ρ 为空气密度，σ 为旋翼桨距角，c 为旋翼弦宽，R 为旋翼弦长，CLα为旋翼升力系数，CDα为旋翼阻力系数。

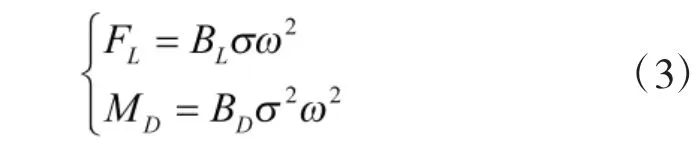
将式（3）代入式（1）可得：

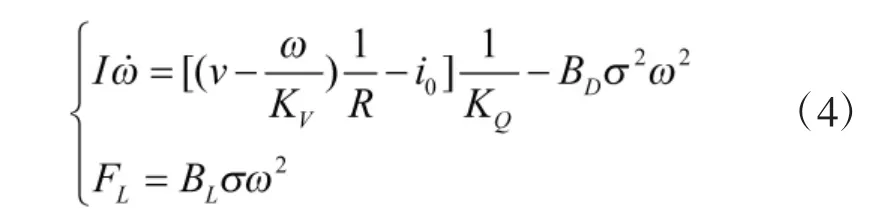
将式（4）在四旋翼飞行器悬停时所需的桨距角σ0与转速ω0进行小扰动线性化：

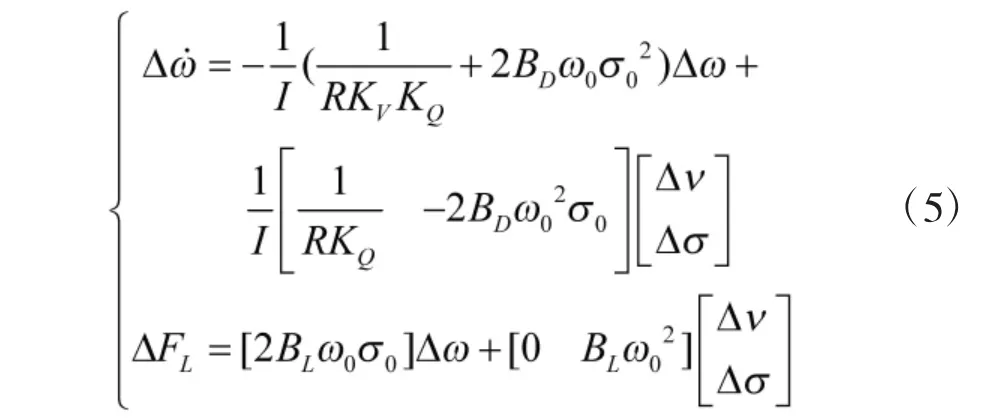
从式（5）可以看出，对于定桨距电机旋翼系统，升力的增加是通过增加直流电机两端的电压Δυ 得到的，升力的改变速度受到电机响应速度的影响。而变桨距电机旋翼系统的升力可以通过改变电压Δυ 和桨距角Δσ 两个因素来改变，如果只考虑改变桨距角，则升力改变的速度将不受限于电机的响应速度。

1.2 变桨距电机旋翼系统控制律

如果不考虑舵机的执行速度，通过直接改变桨距角可瞬间得到需求的升力改变量ΔFLd：

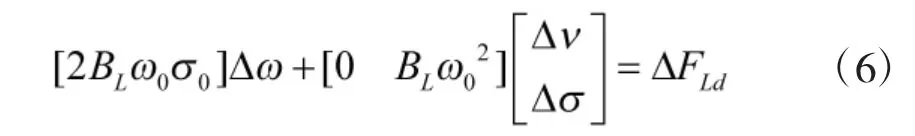
则

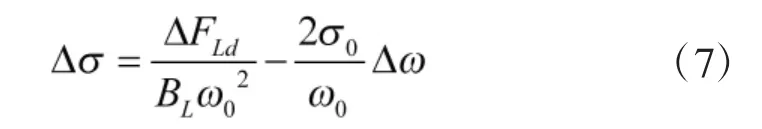
根据式（7），若瞬间得到需求的升力改变量ΔFLd，则需要实时对状态Δω 进行反馈，这会使控制系统结构变得复杂。

现将桨距角改变量Δσ 变为开环形式：

对比式（8）与式（7）可知，若使Δω 尽快保持为0，升力的改变量也会迅速达到ΔFLd。那么，问题转化为将式（8）代入式（5）后，调节电机两边的电压Δυ，使转速的改变量Δω 迅速变为0。

此时，

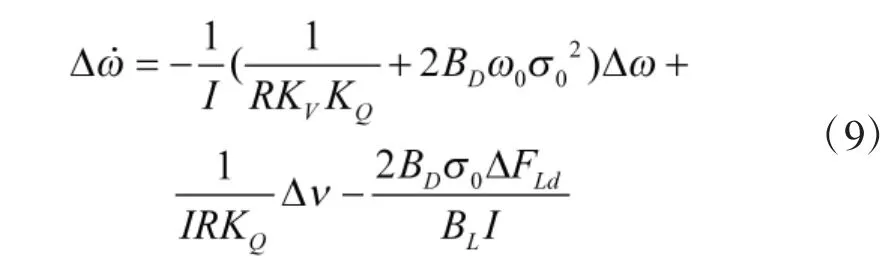
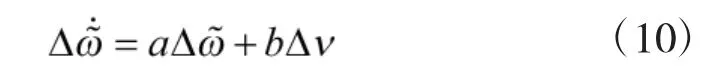
基于状态方程式（10）可将变桨距电机旋翼系统控制问题建模为典型的连续时不变系统有限时间状态跟踪问题：

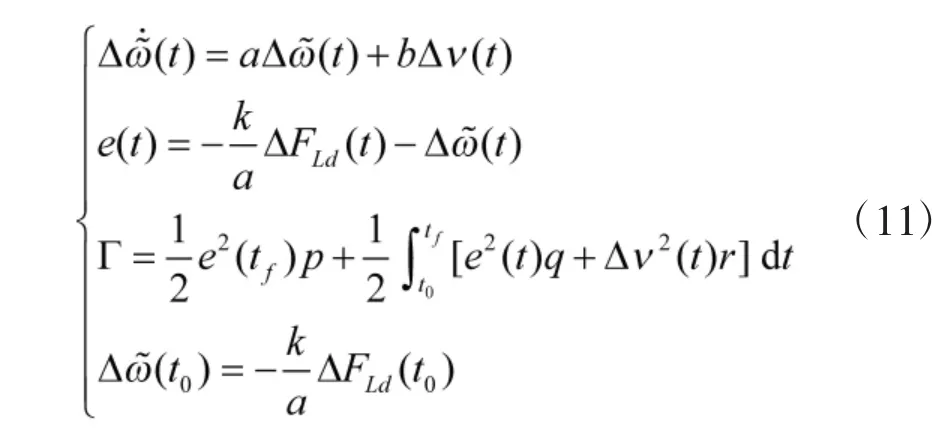
式中，p、q、r 分别为正实数，该模型是在满足状态方程约束与终端约束的条件下，使性能指标Γ最小。

根据最小二次型最优控制求解方法，可得：

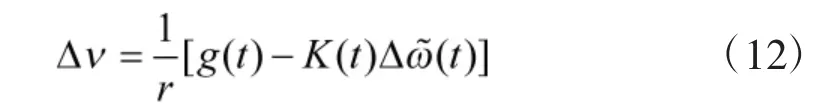
式中，K（t）满足一阶黎卡提微分方程：

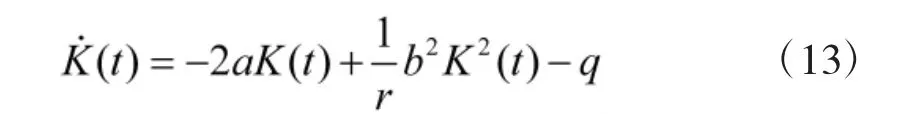
K（t）的边界条件K（tf）=p。

标量函数g（t）满足微分方程：

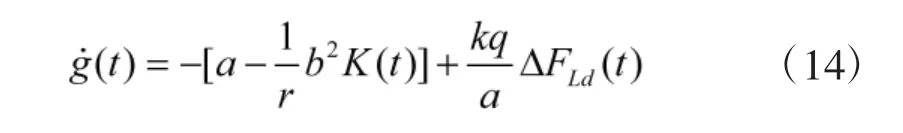
基于上述模型可得到变桨距电机系统结构如图1 所示。

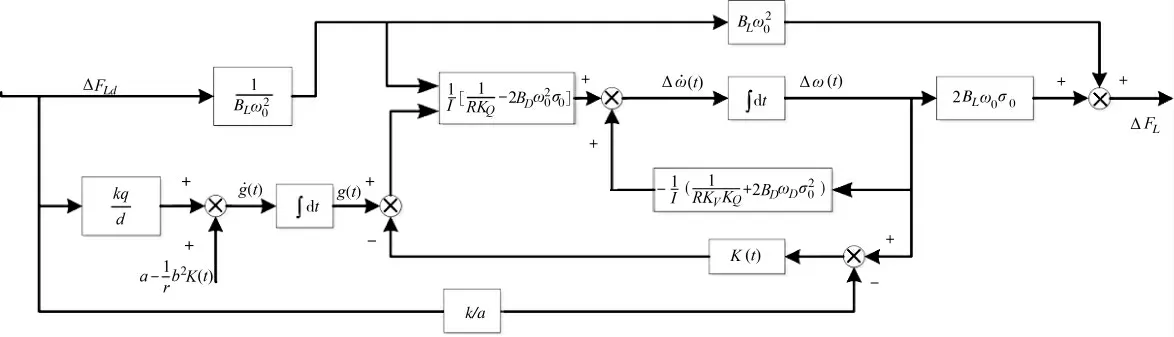
图1 变桨距电机系统结构图

2 变桨距四旋翼飞行器航迹跟踪控制

2.1 四旋翼飞行器动力学模型

定义如图2 所示的地面坐标系OdXdYdZd和机体坐标系ObXbYbZb，其中ObXb轴取为飞行器的速度方向。

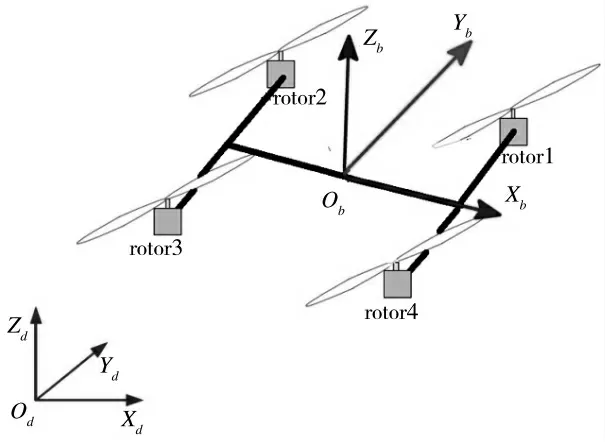
图2 四旋翼飞行器坐标系

四旋翼飞行器动力学模型的建立基于以下假设：

1）飞行器机体为一个刚体；

2）不考虑电机、机架的安装误差，认为飞行器机体为对称分布。

根据牛顿-欧拉方程和四元数运动学，建立模型如下［13］：

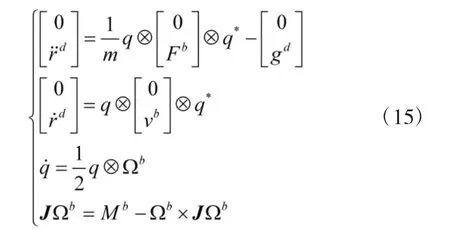
从四旋翼飞行器的特点可知，飞行器受到的除重力外的合外力为4 个旋翼产生的升力之和，方向为沿着轴或其反方向，即

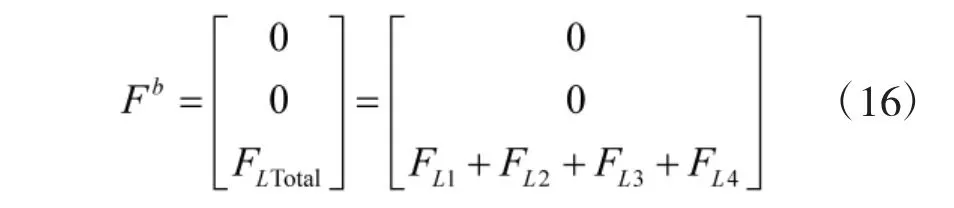
合外力矩Mb有3 个分量，分别为俯仰力矩，横滚力矩和偏航力矩。

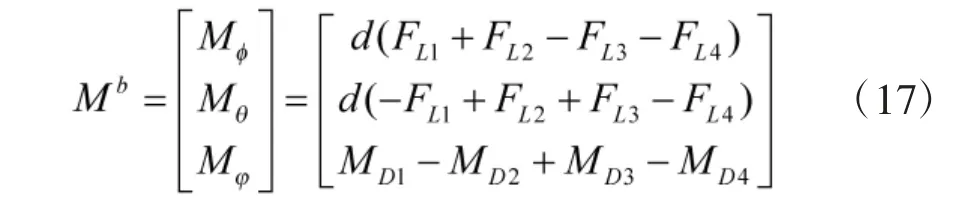
式中，MDi为4 个电机旋翼产生的阻力矩，d 为升力矢量到坐标轴的径向矢量距离。

将式（3）代入式（16）、式（17）可得：

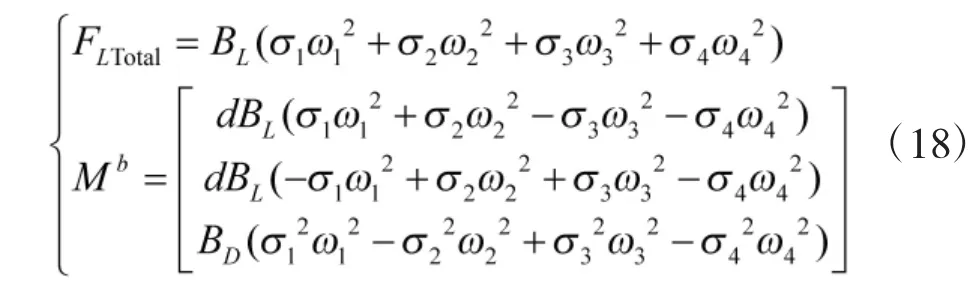
定义控制量U：

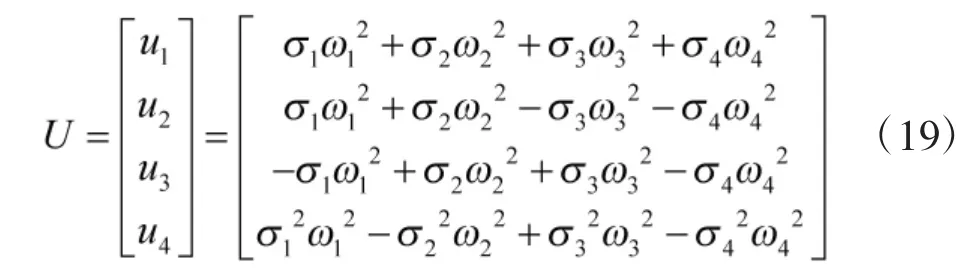
则

根据式（19），若给定桨距角σ 与电机转速ω 的关系，即可通过U 反求出4 个桨距角与4 个转速。前面已证明，变桨距电机旋翼系统使电机转速一直稳定在某一个值时，升力的响应最快，因此，本文假设4 个电机转速全部稳定在固定值ω0。此时，可求解出4 个桨距角：

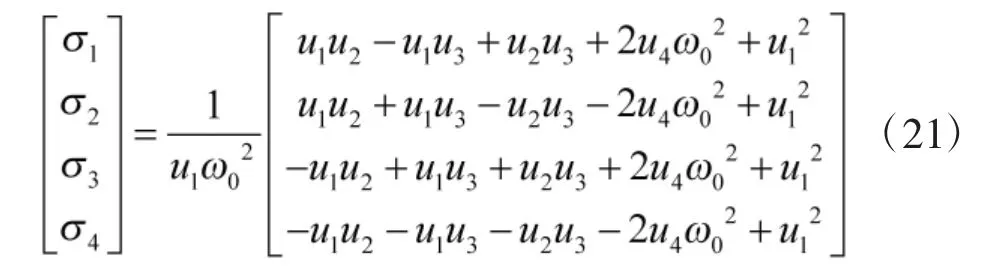
2.2 四旋翼飞行器航迹跟踪控制律

四旋翼飞行器的航迹点为空间离散的状态点，包括位置、速度、加速度信息。本文采用四元数方法来推导四旋翼的航迹跟踪控制律。假设为飞行器提供目标点位置矢量和飞行器的目标偏航角，通过推导控制律，得到飞行器需产生的力与力矩。

运用PID 控制方法［14］，反馈加速度矢量可以表示为：

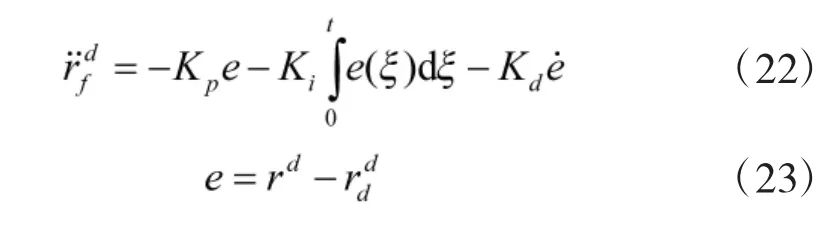
其中，e 为误差距离矢量，rd为当前的位置矢量，为目标位置矢量。进而，可以求出四旋翼受到的合外力Fd：

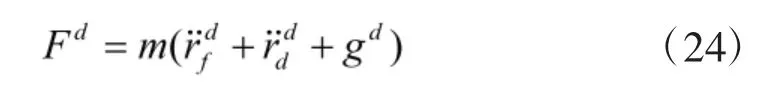
将式（24）代入式（15）可得：

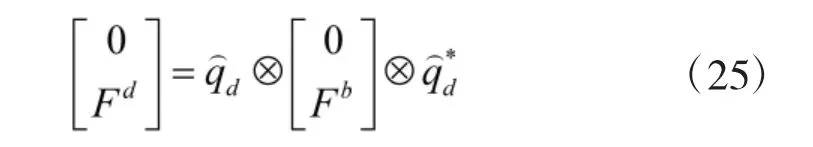
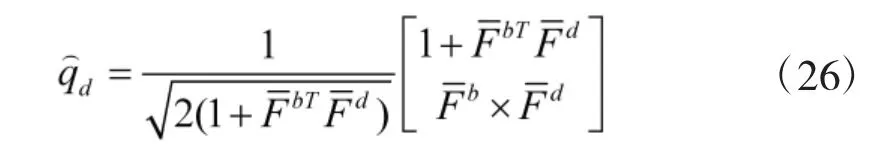
加入目标航偏角，得到目标四元数qd：

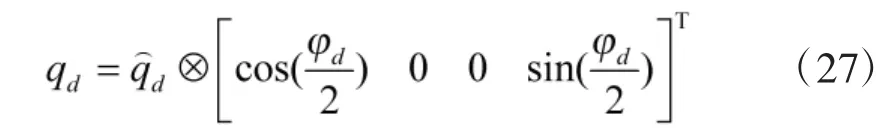
姿态误差四元数qe：

式中，q*为q 的共轭四元数。

下面，推导误差角速度。

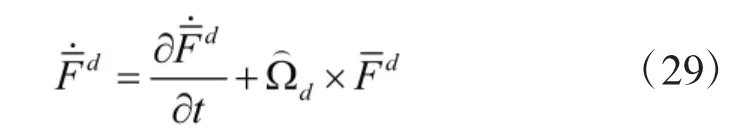
于是，姿态误差角速度Ωd为

其中

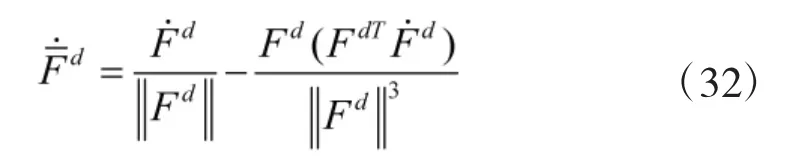
由于单位四元数空间是SO（3）的双覆盖，因此，单位四元数表示姿态误差可能出现标量部分为负的情况，此时可直接将四元数表示的误差转换为其等效表示即可。

根据姿态误差四元数qe与姿态误差角速度Ωd，设计四旋翼飞行器的姿态控制器为：

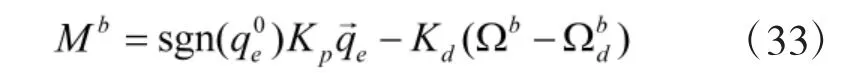
变桨距四旋翼飞行器系统控制结构，如图3所示。

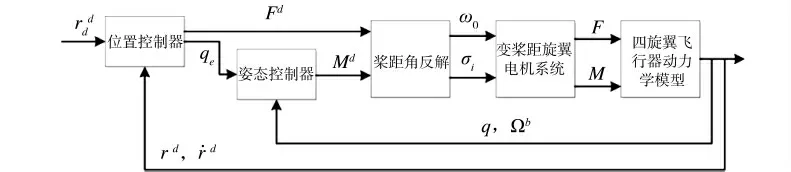
图3 变桨距四旋翼飞行器系统控制结构图

3 仿真实验与分析

3.1 变桨距电机旋翼系统控制仿真

对提出的变桨距电机旋翼系统控制策略的控制性能进行仿真，并与只改变桨距角或只改变电机电压两种控制策略的控制性能进行对比，仿真在MATLAB/Simulink 环境中进行，仿真所用参数如表1 所示。

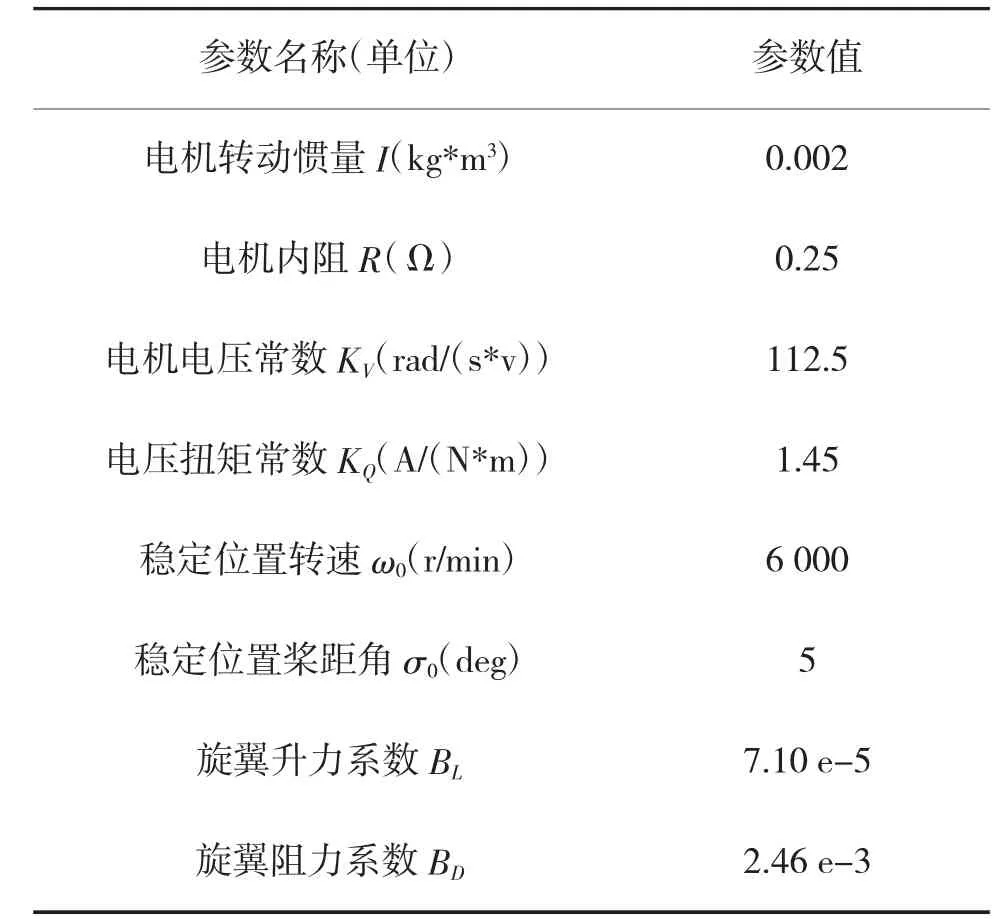
表1 变桨距电机旋翼系统参数表

从图4、图5 所示升力变化曲线、电机转速变化曲线可以看出，只改变桨距角会导致电机转速降低，升力出现较大的超调；而只改变电机两端电压，由于电机的固有动态响应，升力变化缓慢。而本文给出的基于最优控制方法同时改变桨距角和电机电压的控制策略，升力的暂态响应远远优于前两者。

图4 升力变化曲线图

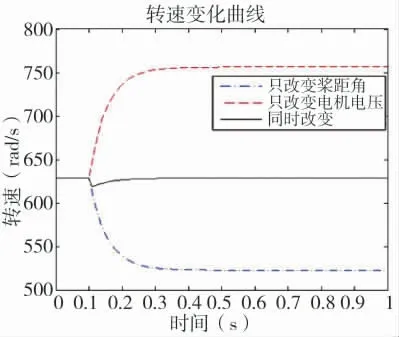
图5 电机转速变化曲线图

3.2 航迹跟踪控制仿真

航迹跟踪控制性能仿真所用的四旋翼飞行器参数如表2 所示。

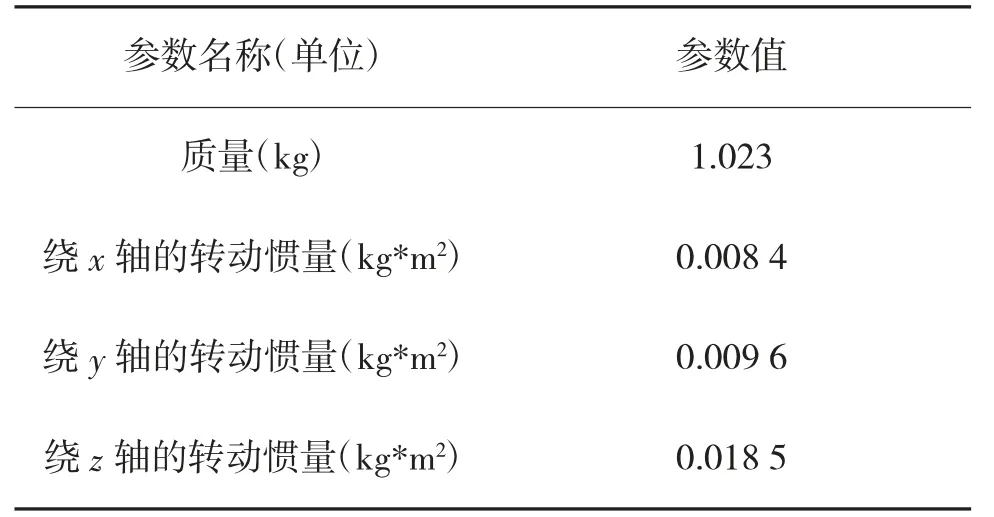
表2 四旋翼飞行器参数表

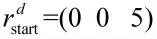
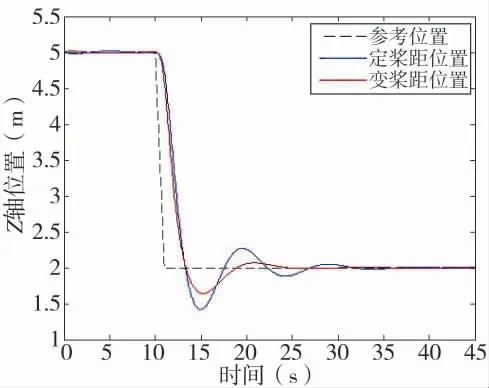
图6 Z 轴位置变换曲线图

仿真2：基于提出的航迹跟踪控制律计算变桨距四旋翼对给定航路的跟踪性能。图7 给出了轨迹跟踪三维图，图8、图9 分别给出了飞行器x 与y 方向的速度位移曲线，仿真结果表明，所设计基于航迹跟踪控制律能够实现变桨距四旋翼飞行器对给定航路的高精度追踪，具有良好的鲁棒飞行能力。

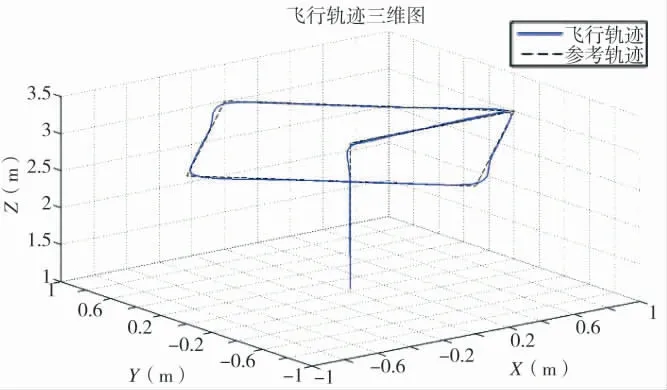
图7 飞行轨迹跟踪三维图

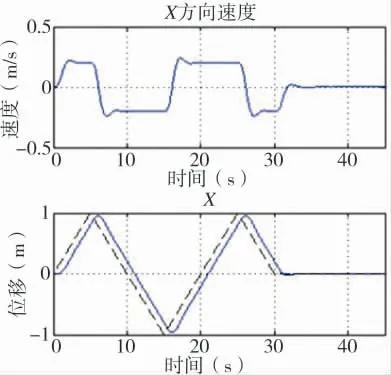
图8 x 方向速度、位移曲线

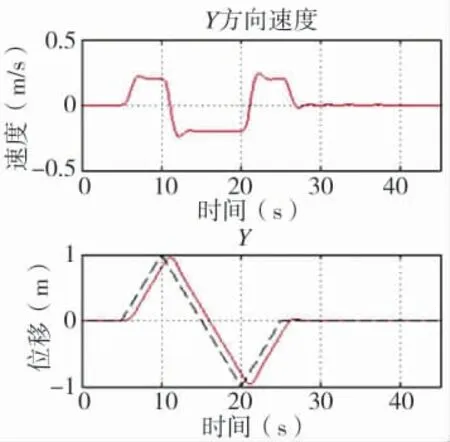
图9 y 方向速度、位移曲线

4 结论

本文在变桨距电机旋翼系统动力学模型的基础上，基于最优控制理论推导出其控制律；运用四元数方法建立了四旋翼飞行器的动力学模型，设计了航迹跟踪控制律，通过仿真验证了变桨距四旋翼飞行器在机动性上要优于定桨距四旋翼飞行器，提出的控制方法能够实现对变桨距四旋翼飞行器的高精度航迹跟踪控制。尽管性能上具有明显优势，但变桨距控制系统结构远比定桨距控制系统复杂，因此，下一步将从飞行试验的层面深入研究变桨距技术在微小型四旋翼飞行器的工程应用问题。