物流企业系统控制中的并联与串联控制比较研究

程伟东+毛良伟+黄垂景

[摘 要]一个实际系统往往是由许多动态环节组成，每个环节输入输出之间的动态关系可用传递关系式来表示，而这些环节又通过串联、并联、反馈等各种形式构成各种复杂的系统。计算是很复杂的，文章介绍了如何通过结构图来简化复杂系统的传递过程的可靠性运算，其推导针对的是普通企业物流控制流程。

[关键词]物流企业；系统控制；并联；串联

[DOI]10.13939/j.cnki.zgsc.2016.32.029

1 串联系统的管理控制过程计算

下面是一个物流采购程序中的串联过程。（见图1）

我们假定这6个环节都是互相完全独立的概率事件，我们要保证这个过程完全正确，只有保证这6个环节都完全正确，才能确保这个过程完全正确，我们假定这6个环节各自正确的概率都是0.9，那要这个过程完全正确的概率是0.9的6次方约为0.53，所以这种串联环节的控制过程发生错误而不被发现的概率是：1-0.53=0.47。

并联系统的管理控制误差计算，而如果我们将上面同样一个采购过程改为并联管理控制流程，其流程设计见图2。

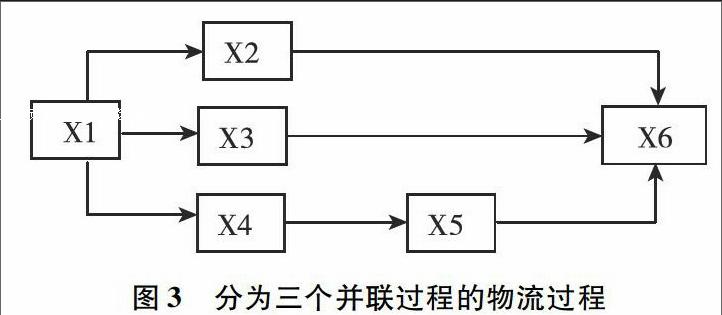
这是一个并联控制系统，它是由两平行作业流程组成，第一个作业流程是签订合同X1—合同登记X2—发货X3—记账X6，假定这一流程各环节都是独立概率事件，每个事件上正确概率都为0.9，那么这一流程正确概率是0.9的4次方约0.66，这一流程错误概率是1-0.66=0.34，第二个作业流程是签订合同X1—财务审核发出收款通知X4一收取货款X5—记账X6，假定这一流程各环节都是独立概率事件，每个事件正确概率都为0.9，那么这第二流程正确的概率也是0.9的4次方约0.66，这第二流程错误的概率是1-0.66=0.34.这个并联管理控制系统和串联控制系统一样是由6个环节组成，但不同的是由两个平行的互相独立的串联控制流程组成，只有这两个独立的串联控制流程都发生错误，整个并联系统才发生错误而不被发现，而这两并行的串联系统发生错误的概率都是0.34，那么整个并联系统发生错误而不被发现的概率是0.34的平方0.34×0.34≈0.12，大大低于串联环节的控制过程的0.47的概率。并且在这个并联控制系统中有两个互相对照的程序，如果从X1→X2→X3和从X1→X4→X5程序来的数字不一样，那么到X6记账程序就会发现不对，所以这个并联过程比串联过程控制更可靠。下面我们将这个物流过程分为三个并联过程（见图3）。

这个并联系统是由三个串联系统组成，第一个串联系统是签订合同X1—合同登记X2—记账X6，第二个串联系统是签订合同X1—发货X3—记账X6，第三个串联系统是签订合同X1—财务审核发出收款通知X4—收款X5—记账X6，假定每个环节正确概率也是0.9，那个第一个串联系统正确概率是0.9的3次方约0.73，错误概率是1-0.73=0.27，第二个串联系统的正确概率也是0.9的3次方约0.73，错误概率是1-0.73=0.27，第三个串联系统的正确概率是0.9的4次方约0.66，错误概率是1-0.66=0.34，这个并联系统由三个独立平行串联系统组成，只有这三个串联系统都发生错误不被发现，整个并联系统发生错误不被发现的概率是3个错误概率的乘积0.27×0.27×0.34≈0.02，大大低于前面两个控制过程的0.47和0.12的概率。因为这三个串联控制系统互相独立，所以三个串联控制系统发生错误不被发现几乎不可能，因为这里有三个互相监控的数据对照系统，从这里我们也可以发现，将一个串联系统分拆成若干个平行的串联系统组成的并联系统，分拆得越多，控制系统错误率越低，可靠性越高，前面在第一个串联系统中数据来源只有一个，无法核对，而在第二个并联系统控制方式和第三个并联系统控制方式中，记账的数据来自独立的两个和三个来源，只有这两个来源数据都一样，或这三个来源的数据都一样，账才可能记下去，否则无法登记，这样就可以发现错误。

2 反馈系统的控制过程计算

假定我们对前面的物流采购程序过程设计反馈控制过程。一种是部分反馈控制过程，一种是全程反馈控制过程。（见图4）

图4显示是部分反馈控制过程，在X1到X2之间实行反馈实际上是X2到X1之间反过来对账，那X1→X2之间流程发生错误不被发现的概率是0.1×0.1=0.01，因为在这个反馈过程中有四种可能，A：第一次正确，第二次错误；B：第一次错误，第二次正确；C：两次都正确；D：两次都错。只有两次都写错同样的数字才能不被发现，所以它的概率是（1-0.9）×（1-0.9）=0.01，那么正确的概率1-0.01=0.99，但是X2→X3→X4→X5→X6过程没有反馈，所以整个过程正确的概率是0.99×0.95≈0.58，错误的概率是1-0.58=0.42，举例来表示就是如无任何反馈X1，签订合同时将价格从正确的80元误写成7元，然后登记合同也跟着登记为7元，一直到记账都登记为7元，因为在电脑和实际手工记账中都是看板生产，根据上一级环节票据登记内容，所以价格写错，以误传误一直误传下去，如果在X1到X2之间加了个反馈程序，不可能合同签订者犯同样错误将价格80元还是写成7元，但是后面的X2→X3→X4→X5→X6程序还是会犯错，所以部分反馈监控程序是不够。

如实行全程反馈监控过程，监控流程如下。（见图5）

如前面所述，从X1→X2正确的概率是0.9，错误概率是0.1，因为有一个反馈环节，两次错误都不被发现的概率是0.1×0.1=0.01，那么正确的概率是0.99，于是从X1到X2正确概率是0.99，如果从X2到X3，X3到X4，X4到X5，X5到X6，全都有反馈全部反过来对账，那么全部正确的概率是0.99的6次方，约等于0.94，错误的概率是1-0.94=0.06，因此反馈环节的控制系统错误发生率大大降低，但是这个反馈环节实际上是12个环节，将这个物流控制系统运行了两次。因此耗费的人力物力也大，所以在实际企业管理内部控制流程中，并联系统及反馈系统的控制可靠性肯定高于串联系统，至于并联系统和反馈系统谁优谁劣，就要具体情况具体分析，根据实际情况决定采用并联或反馈系统了。将财务业务流程拿来讨论，在财务手工记账程序中也是一个并联系统，在这个系统中由审查原始凭证，登记记账凭证等七个程序组成，具体可画图如下（见图6）：

在以上这系统中有两个并行的核算系统，这两个并行的核算系统互相对账在X6，但是从X1至X2很关键，所以一般在X1到X2之间实行反馈监控即反过来对账，从X6到X7可以不搞反馈系统，因为财务报表的内部据结构就是一个互相反馈监控结构，如果试算平衡表数据不对，借货双方不平衡，不管采用账结法还是采用表结法借贷双方都不平衡，而如果损益表的利润数字和资产负债表的利润数不对，那么财务报表就不平衡，这实际也就是混合了串联、并联和反馈的控制过程。

3 目标最优化过程计算

在控制论系统优化的内容里，一般都包括系统目标的内容，也就是当一系统在运行过程中，为达到某目标而设计对系统的控制（决策）变量，这个解答过程称为最优化过程。

例如某跨国公司的商品价格有如下提价数学模型：

根据以往公司的销售统计分析，有如下经验公式：

s（t）=-p（t）+100[SX（]dpt[]dt[SX）]+100

c（t）=0.5S2（t）+2S（t）+40

令： [SX（]dp（t）[]dt[SX）]=u（t），且：p（0）=70， P（52）=100

要求：J=∫520{s（t）p（t）-C（t）}dt→MAX

式中：S（t）表示商品t时刻的销售量，P（t）表示该商品t时刻价格，C（t）表示该商品t时刻的成本，U（t）表示提价变量即决策变量，价格的变化P（0）=70，表示在0时刻（或周）的价格为70元，P（52）表式在52时刻（或周）的价格为100元，又可以说决策开始时价格70元，52时刻（或周）后价格提到100元，并要求提价过程中，使总利润J额最大化，式中S（t）P（t）-C（t）是利润函数，∫x0{s（t）p（t）-C（t）}dx是利润函数的积分，即表示在（0，x）区间内的利润数，本例x=52，经过计算（计算过程略）。

在实际运用中，比较难统计分析的是S（t）和C（t），S（t）表示的是价格和销量之间的积分方程函数关系，C（t）表示的成本与销量之间的一元二次函数关系，这些函数关系都必须统计分析一个企业几年的销量、价格、成本之间的关系才能得出，当建立了这些函数关系式后，利润就不难求得。