统计学课程中方差分析内容的教学方法探讨
陈寿雨


【摘要】针对统计学教学过程中有关方差分析教学内容的重点和难点问题,通过结合一个具体的例子来讲解方差分析的概念、原理和前提条件等知识点,有助于克服方差分析教学内容较为抽象、理论性较强的难点,从而更好地帮助学生理解和掌握方差分析的知识。
【关键词】统计学、教学方法 方差分析(ANOVA ) 莱文方差等同性检验
一、引言
方差分析是一种常用的统计分析方法,属于统计学教学中的重点和难点之一。从统计方法上课,方差分析是较为复杂的一种假设检验的方法,回归分析的结果中也涉及到方差分析的内容,所以对学习统计学课程的学生来说,正确理解和掌握方差分析的思想和原理显然非常重要。但从授课教师的角度,一些教师往往会发现方差分析的内容不好讲,也讲不好,无法让学生较好地理解方差分析的原理。本文基于笔者多年统计学课程教学的经验总结,围绕方差分析的概念、原理和前提条件等教学内容,与同行探讨教学方法。
二、方差分析的概念
方差分析(Analysis of Variance,缩写为ANOVA),是由英国统计与遗传学家,现代统计科学的奠基人之一,R.A.Fisher发明的,用于检验多个总体均值是否全相等的一种统计推断方法。例如,一个国家不同地区的成年男性平均身高是否相等呢?对于该问题的分析就可以使用方差分析的方法。假设该国分为北部、中部和南部等三个区域,成年男性平均身高分别用来表示,则相应零假设和备择假设为:
H0:μ1=μ2=μ3 H1:μj不相等,j=1,2,3
如果最后零假设无法被拒绝,可以得出三个地区成年男性的平均身高不存在显著差异,即地区因素对身高没有影响;反之,如果最后拒绝零假设,从而支持被择假设,则可以得出三个地区成年男生的平均身高存在显著差异,至少有一个地区的平均身高与另一个地区不一样,说明地区因素对身高有影响。因此,方差分析也可以用于研究一个自变量(通常为分类变量)对别一个变量(数值变量)是否有影响的问题。如果只涉及到一个自变量,该方差分析方法称为单因素方差分析,涉及两个自变量则称为双因素方差分析。本文主要围绕单因素方差分析的教学。方差分析的名称容易造成学生的误解,使一些学生误认为方差分析是比较多个总体方差。其实,方差分析是用来比较总体均值是否相同的,但由于使用计算“方差”的方法,故把该方法称作方差分析。
三、方差分析的原理
为了比较多个总体的均值是否相等,方差分析将通过计算样本数据的方差大小进行判断。假设在北部、中部和南部分别随机、独立地抽取一定样本容量的样本,这里为了便于分析,从三地分别抽取3名成年男性,样本容量为9,并记录身高的样本数据,如下图所示。
方差分析就是比较样本数据中北部、中部和南部这三组数据的组间方差和各组数据的组内方差的大小,并构造F检验统计量进行检验。组间方差度量样本数据中组与组之间的变异,从数据结构的角度看表现为数据的横向差异。造成组间数据变异有两个因素,一个是地区因素,另一个是随机因素。组内方差度量样本数据中各组内部的数据变异,是由于抽样的随机性导致,表现为数据的纵向差异。如果组间数据的方差明显地超过组内数据的方差,很可能表明地区因素会显著影响成年男性的身高,从而不同地区成年男性的平均身高存在差异。
为了计算组间方差(MSA),需要先求组间平方和(SSA)和相应的自由度(C-1),其中C为组数,这里为3。组间方差等于组间平方和与相应自由度的比值。
MSA=
组间平方和用每组的均值与所有数据的均值之差的平方再乘以该组观测值的个数来表示。组间平方和越大,说明各组之间的数据差异越大,当然如果组数越多组间平方和也会越大,因此这里不用直接用平方和直接进行比较。
为了计算组内方差(MSW),需要先求组内平方和(SSW)和相应的自由度(N-C),其中N为所有观测值的个数,这里为9。组内方差等于组内平方和与相应自由度的比值。
MSA=
组内平方和用每组的观测值与该组数据的均值之差的平方和来表示。组内平方和越大,说明各组内部的数据差异越大,当然如果各组的观测值越多,则组内平方和也会越大。
有了组间方差和组内方差,就可以造成出F检验统计量,再与临界值比较,可以就以做出统计决策。
FSTAT=
其中,服从分子自由度为C-1,分母自由度为N-C的F分布,其临界值可以在指定显著性水平下通过查表获得。
在样本量较大情况下,手工计算显然耗时耗力,方差分析的相关
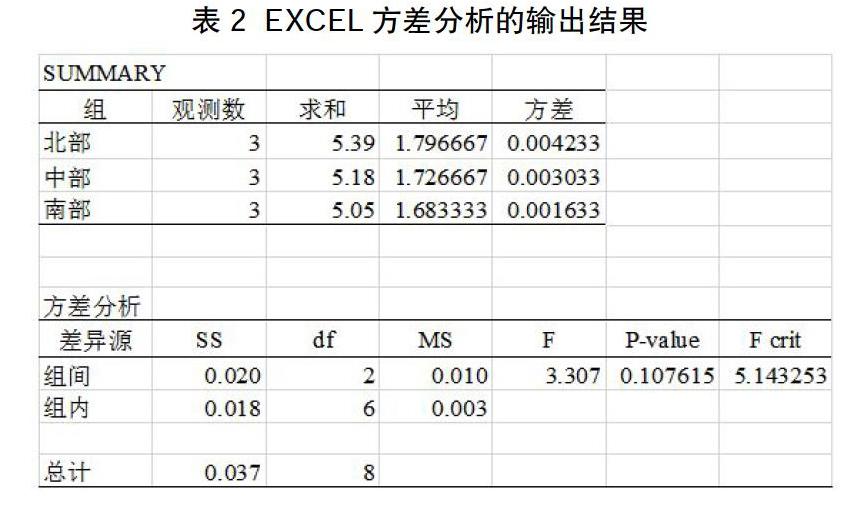
算一般需要通过统计软件来完成。以下是用EXCEL进行方差分析的输出结果。
EXCEL共输出2个表格,第一个表格是对样本数据进行描述分析,从中可以发现各组观测值的个数、均值和方差。第二个表格为方差分析的结果。方差分析把数据的差异区分为组间差异和组间差异,SS为平方差,从表中可以SSA=0.020,SSW=0.018,df为自由度,组间平方和对应的自由度C-1=2,组内平均和对应的自由度为N-C=6。MS为均方,组间均方MSA=0.010,组内均方MSW=0.003。F为检验统计量,其值为MSA/MSW=3.307。在0.05显著性水平下,F的临界值约为5.14。如果使用P值法进行假设检验,EXCEL也给了相应的P值,约为0.108。根据EXCEL单因素方差分析的输出结果,不管使用临界值还是P值法,在0.05的显著性水下,我们都可以得出不拒绝零假设的结论,即三个地区成年男性的平均身高不存在显著差异,同时也表明地区因素没有显著地影响成年男生的身高。
四、方差分析的前提条件
在统计方法的教学过程中,都要强调使用某种统计方法的前提假设条件,如果条件满足,就不能使用相应的统计方法。在方差分析的教学过程中,同样需要强调方差分析的三个前提假设,即样本是随机、独立抽样的,每个总体是正态分布并且方差相等。其中抽样的随机性和独立性相對容易做到,总体是否为正态分布可以通过直方图等方法进行判断。最后总体方差相等是一个非常重要的条件,如果该条件不满足,就不能进行方差分析。如果各总组(各组)本身方差大小存在显著差异,就不能从数据中发现由于地区因素造成的数据变异到底有多大。关于总体同方差假设是否成立可能用莱文方差等同性检验来解决。
莱文方差等同性检验第一步是对各组样本数据排序,找中位数;第二步计算各组观测值与其中位数之差的绝对值;第三步对绝对值做单因素方差分析;第四步得出结论。
根据莱文方差等同性检验的EXCEL输出结果,可以得出三个地区成年男性身高的方差不存在显著差异,可以进行方差分析。
五、小结
针对统计学课程教学中相关方差分析的内容较为抽象、理论性较强的特点,为了帮助学生更好地掌握方差分析的知识,笔者通过多轮的教学实践,认为从具体例子出发,进行启发示教学,比起一开始就讲授方差分析的理论知识,能更利于学生的理解和掌握方差分析的内容。
参考文献:
[1]莱文.商务统计学[M].中国人民大学出版社, 2017.
[2]安德森.经济与商务统计[M]. 机械工业出版社, 2017.
[3]贾俊平.统计学[M]. 中国人民大学出版社, 2018.

