基于SCAD正则最小一乘回归问题研究
罗孝敏,彭定涛
(贵州大学 数学与统计学院,贵州 贵阳 550025)
首先,考虑以下的L0正则最小一乘问题:
(1)

(2)
由于这个问题是NP难的,Candés、Tao等将L0范数松弛为L1范数[2]。L1罚优化问题为:
(3)
2001年,Fan J Q等[3]指出L1正则近似逼近L0正则,得到的结果常有偏估计量。另外,提出用SCAD罚来近似逼近L0罚,并证明了SCAD正则松弛优化问题具有很好的统计性质,例如有orcale 性质,可以用于高维非参数建模;SCAD 罚能够同时实现系数估计和变量选择,其罚函数是对称的,在原点处是奇异的, 在确定的条件下, 其解是连续的,从而具有稀疏性和稳定性;对于较大的系数,SCAD罚函数以确定的常数为界,从而产生无偏估计量[4-5]。2017年,Soubies E等[6]提出了用精确连续L0(CEL0)罚松弛模型(4)来连续逼近问题(2)。精确连续L0罚松弛模型为
(4)

原始基数罚问题:
(5)
其中,A=[A1,…,An]∈Rm×n,Ai∈Rm表示矩阵A的第i列元素组成的向量,b∈Rm。
SCAD罚松弛优化问题为:
(6)
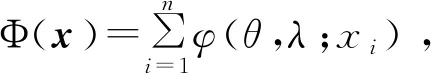
SCAD罚函数满足下列的性质:
(i)当xi>0,φ(θ,λ;xi)是不减的、凹的函数;
(ii)对xi∈R,有φ(θ,λ;xi)>0,及φ(θ,λ;0)=0;
(iii)对∀xi∈R{0},φ(θ,λ;xi)是可微的且有
0≤φ′(θ,λ;xi)≤λ,
这里
图1是一维情形下L0,L1,SCAD罚函数的图像。由SCAD函数的定义及图1可知:当|xi|≤λ时,SCAD罚与L1罚是相同的;当λ<|xi|≤θλ时,随着特征系数|xi|的增大而减小压缩的程度;当|xi|>θλ时,SCAD罚对特征系数不再进行压缩。SCAD罚克服了L1罚有偏估计的缺点[3]。

图1 L0,L1,SCAD函数图像Fig.1 Function images of L0,L1,SCAD
本文主要研究原始基数罚问题(5)和SCAD罚松弛优化问题(6)之间解的关系。第一部分主要介绍需要用到的预备知识;第二部分主要对SCAD罚问题证明了下界理论性质,并在一定条件下,证明了问题(6)与模型(5)有相同的全局最优解以及最优值,松弛模型(6)的局部最优解是问题(5)的局部最优解,且在局部极小值点处问题(5)和问题(6)的最优值是相等的;最后是一个简单的总结。
1 记号
对给定的x*∈Rn,x*的支撑集为
此外,
依次表示向量x的1-范数、2-范数、-范数。

SCAD罚函数的Clarke次微分为:
定义1称x*∈Rn是问题(6)的一阶稳定点,若
命题1若x*∈Rn是问题(6)的局部最优解,则
x*∈Rn是问题(6)的一阶稳定点。

2 SCAD罚松弛问题与原问题解的关系
在这一节里,建立了SCAD松弛问题的下界理论性质,并分析了问题(5)和(6)在一定条件下解(包括局部解和全局解)的关系。


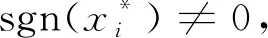
且
故



φ(θ,λ,0)=0≤φ(θ,λ,xi)

φ(θ,λ,0)=0≤φ(θ,λ,xi)≤λ。
因此
φ(θ,λ,xi)≤λ|sign(xi)|。
对上式两边分别求和,有




所以
故




故x*是问题(5)的全局最优解。

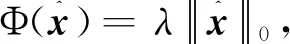



下面研究问题(5)与(6)局部最优解之间的关系。

G(x*)=F(x*)。
证明设x*∈Rn是问题(6)的局部最优解,由命题1可知x*是问题(6)的稳定点。因此,与证明定理1类似可得:
由于x*是问题(6)的局部最优解,故存在x*的邻域N(x*),使得对∀x∈N(x*),有
F(x*)≤F(x)。



因此可知,x*是问题(5)的局部最优解且G(x*)=F(x*),即问题(5)与(6)在x*处有相同的目标值。
定理2表明了问题(6)的局部最优解是问题(5)的局部最优解,在局部最优值点处问题(5)与问题(6)的最优值相等。
最后,在满足一定条件下针对问题(5)与问题(6)解的关系,用图2做一个简短的总结。

图2 问题(5)与(6)的关系Fig2 Relation of between problems(5)and(6)
3 总结
本文主要介绍基于SCAD罚的最小一乘问题(6)与原问题(5)之间解的等价性。证明了松弛模型的下界理论性质,并在此下界理论性质下分析了原问题与松弛问题之间解的等价性。在一定条件下,证明了问题(5)与问题(6)具有相同的全局最优解以及最优值。此外,松弛模型的局部最优解是原问题的局部最优解,在局部极小值点处松弛模型与原问题的最优值是相等的。这为进一步设计有效的算法提供了理论基础。

