一种基于单调链和Geohash索引的公共边裂缝处理算法

杨 伟， 邓涵文， 冯贤菊， 廖雪花， 李晓宁*

（1.四川师范大学计算机科学学院，四川成都610101； 2.河南工业职业技术学院电子信息工程学院，河南南阳473000）

矢量数据压缩在计算机图形学、地理信息系统（GIS）和数字制图等方面的应用非常广泛，其中较为广泛使用的压缩方法为Douglas-Pecucker算法［1］及其一系列的改进算法，其中改进算法大多侧重于算法时间效率的优化［2］、距离阈值的计算［3-4］、自相交和相交拓扑异化问题的处理［5-7］等.在压缩过程中，保持数据的拓扑一致性对数字制图和GIS都至关重要［8］.然而，大多数矢量数据压缩算法在压缩数据时并不考虑数据的空间关系，压缩后出现拓扑关系不一致［9］，如在对共享公共边的无拓扑矢量图形压缩时存在公共边裂缝的拓扑不一致问题.出现这一拓扑异化问题的根本原因是无拓扑矢量图形的共享边被存储多次，当压缩算法对起止点敏感时，共享公共边的两相邻图形因起始点和结束点不同，压缩后导致共享边在2个图形中出现不同的化简结果［10］.如图1（a）所示，多边形 A 与 B 共享顶点｛P6，P7，P8，P9，P1｝，多边形 A、B 经压缩算法化简后，顶点P7从A中删除，但没有从B中删除，公共边｛P6，P7，P8，P9，P1｝在2 个图形中的压缩结果不一致，因而出现图1（b）中的裂缝.

图1 公共边裂缝问题Fig.1 Common edge crack problem

针对这一问题，翟战强等［11］采用穷举搜索思想查找多边形的公共边，对公共边和非公共边分别压缩.王净等［12］采用深度搜索匹配法在整个矢量数据范围内查找公共边，将其从多边形数据中独立出来重组数据，然后用DP算法进行压缩.张胜等［13］采用正向搜索和反向搜索相结合的方法提取公共边生成等效元数据，对元数据压缩后再重建数据并按原格式存储.吴正升等［14］提出一个约束点串建立算法提取公共边的首尾端点，将多边形逻辑分段，然后再压缩各个分段.同文献［12-13］的方法相比，文献［14］的算法所需辅助空间较少，但公共边被多次压缩，因而时间效率不高.谢亦才等［15］利用字符串的模式匹配算法（KMP算法）提取公共边，根据公共边对象的压缩标记保证公共边只压缩1次.金良益等［16］指出了深度搜索匹配法提取公共边的不足，提出了一种基于共线搜索匹配的公共边提取算法.此外，金良益［17］将公共边的提取转化为找最长公共子串，提出了一种基于动态规划的无拓扑矢量化多边形公共边提取算法.赵真等［18］提出了考虑空间对象拓扑关系的压缩算法，保留了拓扑关系，解决了公共边压缩后出现裂缝的问题.

上述文献均采取化简前提取多边形的公共边，对公共边和非公共边分别压缩的策略，保证公共边去除的顶点保持一致.该类算法虽可解决公共边裂缝问题，但时间效率比较低，主要原因有以下3点：

1）每个矢量图形均需要同其他矢量图形进行是否相交判断，假设矢量图形数为m，则相交判断的时间复杂度为O（m2）；

2）提取公共顶点的方法大都采用双向深度搜索匹配法、模式匹配算法或动态规划算法，这一类算法在搜索多边形数量较多时效率不高；

3）公共边在压缩时可能被压缩处理多次.

原因2）为制约算法效率的关键.为解决上述问题，本文提出了一种基于单调链和Geohash索引的公共边裂缝处理算法.

针对以往模型做了以下3点改进：

针对1），为了避免在整个图形集中进行相交图形的判断，本文采用单调链扫描线算法，通过建立矢量图形单调链，提前过滤掉了大量相离图形，大大减少需要进行相交判断的矢量图形数，一定程度上提高了算法效率；

针对2），本文利用Geohash编码长于快速搜索的特性，构建Geohash索引结构，将空间划分为一个个矩形区域，实现两相交图形的公共顶点快速查找，大大提高了公共点的查找速率；

针对3），设计了一个索引结构存储公共边的压缩信息，当检索到公共边已被压缩过时，则直接根据索引结构提取公共边的第一次压缩数据，在保证公共边只压缩一次的条件下保证图形的完整性和一致性.

1 基于单调链和Geohash索引的公共边裂缝处理算法

基于单调链的扫描线算法常用于平面线段集合求交中过滤大量候选线段［19］.基于此，本文将其应用于矢量图形集的预处理，用于从众多的矢量图形中挑选出可能与当前图形相交的矢量图形.其次，对每个矢量图形，计算每个顶点的Geohash编码，创建Geohash索引表.然后，利用Geohash索引快速查找的特性，根据图形的相交图形，在图形中找到公共点和非公共点，并据此将矢量图形划分为公共边集合和非公共边集合.最后，对公共边和非公共边分段压缩时，对压缩过的公共边建立索引，保证公共边只压缩一次.

算法可粗略分为初始化图形单调链、生成相交图形集、建立Geohash索引表、提取公共边和分段压缩5个步骤.依次详述如下.

1.1 初始化图形单调链单调链扫描线算法的前提就是生成矢量图形的单调链.为此，本文利用堆排序算法，根据每个矢量图形的最小外接矩形MBR（Minimum Bounding Rectangle）的最小横坐标 xmin对图形集进行排序，生成一个xmin值由小到大的单调链，记为 MC（Monotonic Chain）.MC 中图形的xmin单增，如果多个图形的xmin相同，则按其最小纵坐标ymin由小到大排序.如图2所示的矢量图形集｛A，B，C，D，E，F，G｝，排序后生成的图形单调链 MC为｛A，D，B，E，C，F，G｝.

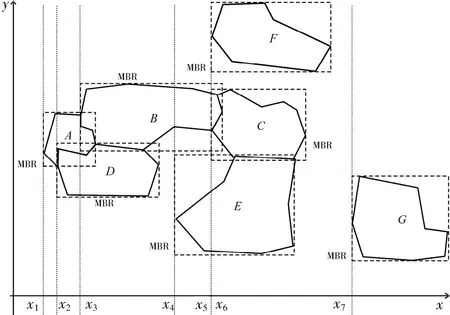
图2 图形集示例Fig.2 A graphics set example

1.2 生成相交图形集基于生成的单调链MC，利用扫描线算法扫描单调链MC中的矢量图形，确定每个图形的相交图形集.涉及的数据结构有：MC，含义同上；AC（Active Chain）记录同当前扫描线相交的矢量图形集合；RS（Related Shapes）为图形的相交图形集.

设单调链MC中有k个图形，过每个图形Si的MBR 的 xmin做纵向扫描线，记为 xi（i＝1，2，…，k）.初始化AC＝｛｝，对每一个xi，依次执行如下步骤：

1）如果AC中图形的MBR的xmax≤xi，从AC中删除该图形；

2）将该图形Si插入AC；

3）将新插入图形Si，同AC中已有图形逐一进行最小外接矩形的相交判断，若AC中已有图形与新插入图形Si相交，则将该图形保存在新插入图形Si的相交图形列表RS中.

表1以图2所示的图形集为例，说明生成相交图形集的执行过程.图形C、F的MBR的xmin相同，所以扫描线x5和扫描线x6相同，分别代表图形C、F生成相交图形列表的过程.

通过上述扫描过程，可以过滤掉大量相离图形，快速确定每个矢量图形的相交图形.结束扫描后，每个图形都生成一个列表RS，记录了与自己相交的所有矢量图形，为下一步的公共边提取处理提供了基础数据.

表1 相交图形集的生成过程Tab.1 Generation process of intersecting graphics sets

1.3 建立Geohash索引表Geohash编码将二维的经纬度坐标编码成一维的字符串，在实现邻近点搜索时具有快速查找的显著优势［20］.Geohash编码技术广泛应用于空间数据的检索，其编码过程实际上是将区域划分为一个个规则矩形，并对每个矩形进行base32编码.Geohash编码长度越长，区域划分越细，搜索时的效率越高.例如经纬度坐标为（116.389 550，39.928 167）的空间点，按 Geohash 编码生成的二进制序列为11100 11101 00100 01111，按base32编码为wx4g，实际上是表明该点落在wx4g代表的矩形区域.

Geohash索引表的建立的过程如下：

对MC中每一个图形Si，初始化一个Hash表HTi为空.对图形Si中的每一个顶点Vk，

1）计算顶点Vk的Geohash编码Code；

2）若Code在索引表HTi的表项中已存在，则将坐标点插入到Geohash编码对应的链表之后，否则在索引表中新增一项，并保存Geohash编码和坐标点到该项对应的链表.

按上述算法，MC中每一个图形都会生成一个类似图3的Geohash表.Geohash索引表中的每一项都由键值Geohash编码及其对应的坐标点链表组成，链表中存放Geohash编码相同的坐标点，提供了Geohash编码和坐标点之间的映射关系.

图3 Geohash索引表示例图Fig.3 Example diagram of Geohash index table

通过键值Geohash编码来检索落在某个区域的坐标点，只需搜索Geohash编码对应的链表中的坐标点即可，速度非常快.当编码长度较大时，链表中的坐标点个数接近于1，检索坐标点的时间复杂度接近于 O（1）.

1.4 公共边提取公共边提取的前提是公共点的判断.根据上一节为每个图形建立的Geohash表，对于相交的2个图形A和B，判断A上一点point是否为A和B的公共点的方法如下：

1）计算点point的Geohash编码，假设为code2；

2）在图形B的Geohash索引表中查找key值为code2的项.如找到，转3）；如未找到，point为图形A、B的非公共点；

3）找到该项对应的坐标点链表（如图4中虚线框部分），比较point与链表中的点坐标是否相同.若相同，则point为公共点，否则为非公共点.

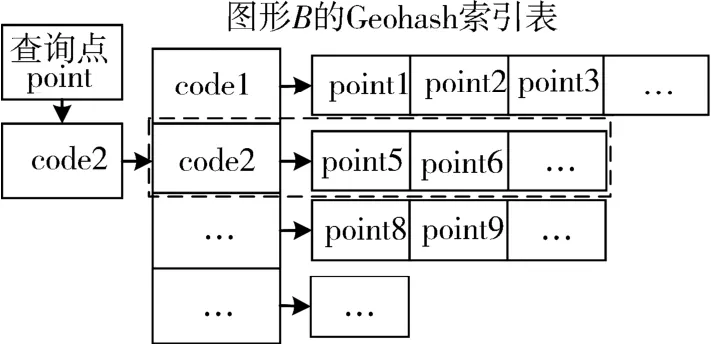
图4 公共点查找示意图Fig.4 Example diagram of finding common points

公共边提取实质上是公共边端点的查找.假如端点已经确定，以之作为约束点，即可在约束点处将多边形从逻辑上分段，拆分为公共边和非公共边.

假设图形 A 顶点记为 ai，i＝1，2，…，m；图形 B为 A 的一个相交图形，其顶点记为 bj，j＝1，2，…，n.图形A中的有2个相邻顶点ai和ai-1，根据2个相邻顶点是否是公共点这一特性，可划分为4种可能：

1）若ai为公共点且ai-1为非公共点，则ai为公共边的端点.ai和图形B中与ai坐标相同的顶点bj分别为图形A和B的拆分点，如图5（a）.

2）若ai为非公共点且ai-1为公共点，则ai-1为公共边的端点，ai-1和图形B中与ai-1坐标相同的顶点bk分别为图形A和B的拆分点，如图5（b）.

3）若ai、ai-1均为公共点，则需进一步判断图形B 中ai、ai-1对应的公共点bj、bk是否连续（包括正向连续或反向连续），若不连续，则ai-1、ai为公共边的端点，ai-1、bk和 ai、bj均为图形 A、B 的拆分点，如图5（c）；若连续，则 ai不是端点，ai-1是否为端点尚需结合ai-2是否为公共点来判断.

4）若 ai、ai-1均为非公共点，则 ai、ai-1均不是公共边的端点.

图5 公共边首尾点的3种情况Fig.5 Three kinds of end point cases on common edge

记sorta、sortb为记录图形A、B所有公共边首尾点下标的有序链表.假设ai为公共点，bj为B中与ai坐标相同的公共点；ai-1为公共点，bk为B中与ai-1坐标相同的公共点，初始化i＝1.根据上面的公共点判断规则，在2个相交矢量图形中查找公共边端点的主要步骤如下：

1）读取矢量图形 A（a1，a2，…，ai，…，am）、B（b1，b2，…，bj，…，bn）.

2）读取矢量图形 A 上点 ai（i＝1，2，…，m）的Geohash编码.

3）根据上面的公共点判断方法，判断ai是否为公共点.若ai为公共点，转4）；若ai为非公共点，转 6）.

4）若ai-1为非公共点，则ai为公共边的端点，ai、bj应为拆分点（如图6中的的情况），将其下标存储在各自的排序表sorta、sortb，否则转5）.

5）若 i＝m，则 ai为公共边的端点，ai、bj为拆分点，将其下标存储在各自的排序表sorta、sortb，转7）；否则进一步判断bj下标同bk下标是否连续，即｜j-k｜是否等于 1，若不连续（｜j-k｜！＝1），则 ai、ai-1为公共边的端点，ai-1、bk和 ai、bj均为拆分点，将其下标存储在各自的排序表sorta、sortb，转7）.

6）若ai-1为公共点，则ai-1为公共边界的端点，ai-1、bk为拆分点（如图6中的的情况），将其下标存储在各自的排序表sorta、sortb；否则，转7）.

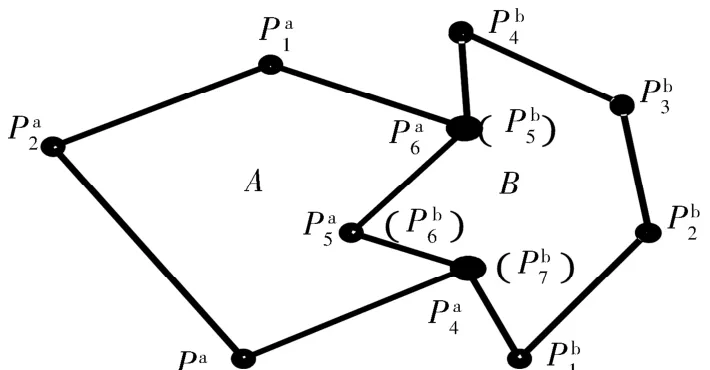
图6 公共边首尾端点的标记Fig.6 Mark the ends of common edge

7）i＋ ＋，若 i＞m 结束；否则，转2）.

待所有图形处理完，每个图形可得到一个记录图形拆分点下标的有序链表sort.根据这个有序链表对图形进行逻辑分段，就可将图形分为公共边和非公共边.如图6所示，图形A得到的有序链表为｛4，6｝，可将其拆分成下标为1 ～4、4 ～6、6 ～1 的3个逻辑分段；图形B的有序链表为｛5，7｝，可将其拆分成下标为1～5、5～7、7～1的3个逻辑分段.

1.5 分段压缩基于上一小节的提取结果，可将每个图形逻辑分段为公共边和非公共边，依次对每个分段进行压缩，能够解决公共边裂缝的问题.但公共边在共边图形中至少出现2次，出于效率考虑的原因，希望其只被压缩1次.为实现上述目的，并且保证所有共边图形的完整性和一致性，本文设计了一个索引结构表，用于为一个图形保存有关公共边压缩的索引信息，如图7所示.

图7 公共边压缩信息索引表Fig.7 Index table of common edge compression information

信息索引结构表中每个元素保存每条公共边有关压缩的必要信息，元素由（key，Value）键值对构成.其中key为公共边压缩前首点在原链表中的索引号；Value有2个数据段，一个为该公共边压缩后首点在新链表中的索引号Indexafter，另一个为公共边压缩后顶点的数量length.当图形未被压缩时，索引表为空；有公共边被压缩后，索引表记录了图形中公共边的压缩结果.

图6所示的图形A，只具有一条公共边，其首尾点分别为｛4，6｝.假设该公共边第一次压缩，压缩后非公共边1～4由4个点约简为3个点，公共边4～6由3个点约简为2个点，则A需要维护图7所示的压缩信息索引表，表中只有一个元素，其（key，Value）分别为（4，（3，2））.

分段压缩时，首先根据有序链表数据将原点链表分解为多个逻辑分段.对于每一个分段，执行如下步骤：

1）如果该段为非公共边，直接调用压缩算法.

2）如果为公共边，首先根据其首尾点索引号j、k找到其在共边图形中的对应索引号l、m.以l、m的最小值min（l，m）作为键值，在共边图形的压缩信息索引表中查找该项是否存在.如果不存在，该公共边未被压缩，转3）；如果存在，该公共边已被压缩，转4）.

3）直接调用压缩算法，并保存该公共边的压缩索引信息到图形的公共边压缩信息索引表.

4）根据该项的Value，从共边图形压缩后的顶点链表中，直接拷贝或者反序拷贝从Indexafter开始的length个顶点作为压缩结果.

根据公共边首尾点索引号j、k查找其在共边图形中的对应索引号l、m时，有可能会出现反序情况，如图6所示，A中的公共边顶点序号｛4，6｝在B中对应为｛7，5｝.在查找索引信息时，需根据较小值｛5｝作为查找的键值，同时拷贝公共边压缩数据时也需要反序.

1.6 算法整体流程综上所述，从多个图形对象中提取公共边和非公共边的算法流程如下：

1）对矢量图形集进行堆排序，获得图形集的单调链MC.

2）通过扫描线算法扫描上述单调链MC，确定每个图形的相交图形列表RS.

3）构建所有图形的Geohash索引.

4）相交图形公共点的查找和标记.遍历每个图形，查找图形和其相交图形列表RS中所有图形的公共点，根据公共边首尾端点的判断规则，标记公共边的首尾公共点、逻辑分段公共边和非公共边.

5）分段压缩.

设shapes为所有图形的集合；MC为根据图形最小包围盒构建的单调链；AC为活动图形链；RS［i］为第 i个图形的相交图形列表；HeapSort（shapes）用于生成图形的单调链，其详细的处理流程参见本文1.1 小节；CheckCross（e，s）用于判断图形 e、s的最小外接矩形是否相交；GeohashTable（s）用于为图形s建立Geohash索引表，其详细的处理流程参见本文 1.3 小节；MarkEndPoint（s，e）用于标记图形s、e的公共边端点，其详细的处理流程参见本文1.4小节；Compress（s）用于压缩图形 s中的各个分段，其详细的处理流程参见本文1.5小节.算法伪码如下：

Input：shapes，vector graphics set and points have no labels

Ouput：shapes，vector graphics set and points have labels

Initializations：

-MC：monotonic chain of shapes，initialized to null；

-AC：active chain of shapes，initialized to null；

For every shape s in shapes｛

／*Compute Minimum Bounding Rectangle*／

Compute MBR（s）；

｝

／*Sort shapes in the increasing order of the minimum x coordinate of its MBR and the minimum y coordinate if minimum x coordinates are equal*／

MC←HeapSort（shapes）；

／*Build relative shapes collection for every shape in MC*／

M←count of shapes in MC；

For i←1 to M｛

／*initialized related shapes set of the i th element of MC*／

RS［i］＝null；

s←MC ［i］；／*the i th element of MC*／

／*the minimum x coordinate of MBR of shape s；

x←s.MBR.xmin；

For every shape e∈AC｛

If e.MBR.xmax≤x then delete e from AC；

｝

For every shape e∈AC ｛

If CheckCross（e，s）then insert（RS［i］，e）；

｝

insert（AC，s）；

｝

／*Construct Geohash Table for every shape in MC*／

For every shape s in MC｛

GeohashTable（s）；

｝

／*Label all end pointsfor every shape

For every shape s in MC｛

For every shape e in RSof shape s｛

／*Find and label end points of shape s and e

MarkEndPoint（s，e）

｝｝

／*Compress every shape sectionally

For every shape s in MC｛

／*Compress every shape s

Compress（s）

｝

2 实验结果及分析

本文选取了3个数据集，实现了算法以验证算法的性能.数据集分别为：中国省级行政界线Data1，世界地图中的国家行政界线Data2，中国县级行政界线Data3.3个真实矢量地图数据集分别代表了不同数量等级和不同分布状态的地图数据，其参数如表2所示.

实验环境如下，处理器：Intel（R）Core（TM）i7-7700HQ CPU ＠ 2.80 GHz；内存：8.00 GB.

表2 测试数据集参数列表Tab.2 Parameter list of three test data sets

2.1 公共边提取与否对数据压缩影响的定性分析针对上述3个数据集，本文采用经典Douglas-Peucker算法作为压缩算法，对比直接进行压缩处理的化简结果和经本文算法做公共边预处理后再压缩的结果.总的说来，本文的公共边提取算法，能够保证公共边的化简结果一致，解决公共边裂缝问题.

图8给出了中国省级行政界线数据未做公共边预处理和做公共边预处理后压缩结果的局部放大对比示例.图8（a）中的粗实线为未做公共边提取的压缩结果，图8（b）中的虚线为采用本文算法做公共边提取后的压缩结果.从局部放大图可以看出，图8（a）中圆圈部位发生了裂缝，而图8（b）则保持了2段公共边的化简结果一致.

图9给出了世界地图国家行政界线数据未做公共边预处理和做公共边预处理后压缩的局部放大对比示例.图9（a）中粗实线为未做公共边提取的压缩结果，图9（b）中的虚线为采用本文算法做公共边提取后的压缩结果.圆圈内国家行政边界与多国接壤，圈内线段均为公共边.从圆圈的局部放大图可以看出，图9（a）中圆圈部分粗实线线条多为双线，表明多处公共边被压缩成不同的结果，而图9（b）则保持了多段公共边的化简结果一致.

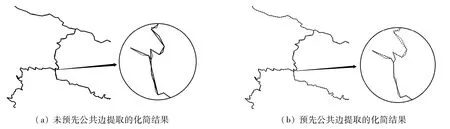
图8 测试数据集Data1在2种情况下的化简结果Fig.8 Different simplified results with or without extraction of common edges in Data1 set

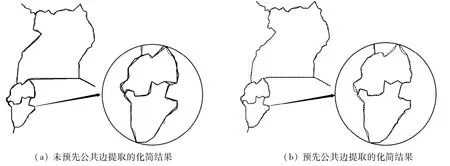
图9 测试数据集Data2在2种情况下的化简结果Fig.9 Different simplified results with or without extraction of common edges in Data2 set

从实验结果来看，采用本文算法预先处理相邻图形的公共边，可以保证公共边在相邻图形中化简结果的一致，解决常见的公共边裂缝问题.值得注意的是，虽然都采用DP算法作为压缩算法，但因为公共边被拆分后，输入DP算法处理流程的数据首尾点发生了变化，导致公共边提取后的压缩结果与不预先提取公共边的结果有些细微变化.

2.2 算法的时间效率分析本文算法中涉及公共边提取和分段压缩2个部分，其中分段压缩部分，其时间效率受压缩算法的选取而不同，所以在时间效率分析上仅对公共边提取部分的时间效率进行分析.假设M为图形集中的图形总数，N为图形集中总的顶点个数，m为扫描次数（最坏情况下为图形总数M），k为每次扫描要处理的图形最大值（k≪M），ni为图形i的顶点总数，ki为图形i的RS集合中包含的图形数，L为Geohash编码长度，S为Geohash编码对应矩形区域所包含的点数的最大值，则公共边提取算法的4个环节的时间复杂度分别为：

1）初始化图形单调链，时间复杂度为O（M log2M）.

2）生成每个图形的相交图形集合RS，时间复杂度为O（k*m）.

4）公共边的提取.需要遍历每个图形，查找图形和相交图形集合RS中图形的公共点，标记首尾公共点.对于图形i，判断其上所有点是否为公共点共需要ni*ki*S次判断，那么M个图形总的时间复杂度为

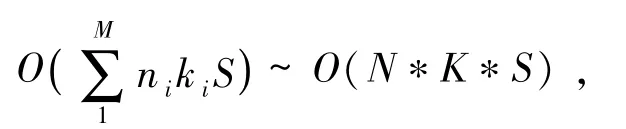
其中，K＝max（ki），K≪M.

综上，算法公共边提取的时间复杂度为

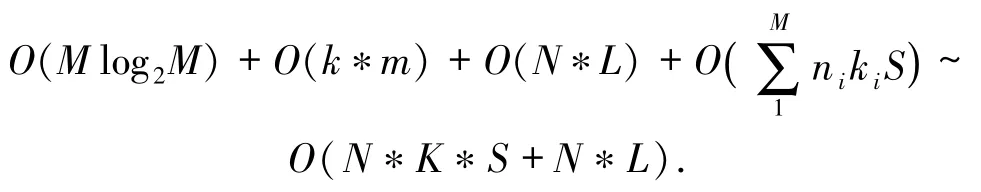
2.2.1 Geohash编码长度对时间效率的影响 Geo-hash编码在算法中的作用是减小公共点的搜索范围.Geohash编码长度L决定了搜索空间大小，是影响算法时间效率的重要因素.为测试编码长度L对算法时间效率的影响，本文用1～9的编码长度对3组数据集进行了公共边提取实验，其实验结果如表3所示.可以看出，随着编码长度L的增加，提取公共边的时间总体上呈先下降后上升的趋势.这是因为随着编码长度L的增加，每个编码所对应的矩形区域和落入该区域的顶点数越来越小，也就是说Geohash索引表中的顶点链表越来越短，查找公共点所花费的时间越来越少.在极限状态下，每个编码所对应的矩形区域最多只包含1个数据点，此时公共点的查找时间最短.此后，编码长度的增加对于公共点查找时间没有影响，但构建索引的时间一直随编码长度单调递增.因此，提取公共边的时间总体上呈先下降后上升的趋势.在实际应用中，由于数据采集精度的限制，无论数据的体量大小、稀疏程度，编码长度较为合适的取值范围为4～6.例如，数据集Data1，顶点数在万级规模，编码长度为5时，提取公共边耗时最小，为45.72 ms；数据集Data2，顶点数在十万级规模，编码长度为4时，提取公共边耗时最小，为102.31 ms；数据集Data3，顶点数在百万级规模，编码长度为5时，提取公共边耗时最小，为 1 246.22 ms.

同样可以看出，提取公共边所需的时间与数据规模成正向关系.在同一编码长度下，随着数据集顶点数、图形数量的增加，提取公共边所需时间也总体呈上升趋势.在编码长度为2～3时，数据集Data1提取公共边所需时间明显大于Data2的处理时间.这主要是因为Data1的图形比较紧凑，每个图形的相交图形个数K较大的缘故.

2.2.2 算法时间效率的对比实验与分析 为进一步验证算法的时间效率，本文选用文献［14，17］算法和本文算法进行对比，其实验结果如表4所示.

可以看出，当Geohash编码长度范围为4～6区间，本文算法的时间效率明显优于文献［17］的动态规划算法和文献［14］的深度搜索算法.

表3 不同编码长度、数据量和图形分布状态下的公共边提取时间Tab.3 Common edge extraction time under different encoding lengths，data amounts，and graphics distribution ms

表4 3个不同算法的公共边提取时间Tab.4 Common edge extraction time using three different algorithms ms

此外，本文还对公共边压缩一次和未作公共边压缩次数约束的时间效率进行对比，其结果如表5所示.设t0为公共边压缩次数未限制的压缩时间，t1为公共边压缩一次的压缩时间，时间减少率定义为（t1-t0）／t0.

可以看出，限定公共边压缩1次时，算法的效率也有一定的提高.但是对不同的数据集，效率提升不同.例如，差不多的压缩率情况下，对数据集Data3，做了公共边压缩次数限定后，时间减少90.02%.而数据集Data2，做了同样的处理，时间仅减少了19.92%.这可能跟数据集中公共边的数量有关.

表5 公共边压缩次数处理前后的不同压缩时间Tab.5 Different compression time before and after limiting common edge compression times

综上，实验结果说明了本文的公共边提取算法，不仅能够有效地解决公共边裂缝问题，在时间效率上也具有较大的优越性.

3 结论

本文在分析多矢量数据压缩时产生公共边裂缝的原因，以及解决该问题的常用方法的优缺点的基础上，提出了一种基于单调链和Geohash的公共边裂缝处理算法，并通过实验验证了本文算法在解决裂缝问题上的有效性，对比分析了本文算法的时间效率.

本文还设计了一个公共边压缩信息索引表，用于公共边多次压缩时直接从第一次压缩结果中提取数据，从实验结果看，经过该环节处理后，压缩时间也有比较明显地减少.

本文算法不局限于任何压缩算法，可作为一个预处理过程，在压缩前对矢量数据进行逻辑分段，保证公共边压缩结果的一致性，从而解决公共边裂缝问题.从实验结果可以看出，Geohash编码长度对于公共边提取过程的时间效率的影响比较大，而本文仅从数据采集精度的角度给出了编码长度的一个适当范围，未涉及如何自适应的确定编码长度这一问题，未来需进一步研究讨论.

此外，本文算法在实现过程中，未过多考虑数据结构与算法的优化，如果进一步优化算法与数据结构，在时间效率上和空间效率上应当有提升的空间.