基于粗糙熵的三支加权变形熵

廖升俊， 张贤勇*， 莫智文， 唐玲玉

（1.四川师范大学数学科学学院，四川成都610066； 2.四川师范大学智能信息与量子信息研究所，四川成都610066）

由波兰学者Pawlak教授提出的粗糙集理论［1］是分析不完整、不精确信息系统的有力工具.目前，粗糙集理论已经广泛应用于信息系统分析、人工智能、数据挖掘、模式识别等领域.

在粗糙集理论中，已经引入熵测度［2］.文献［3］在粗糙集理论中定义了粗糙熵；文献［4］对粗糙熵进行了进一步研究，重新定义了粗糙熵的表达式；文献［5］对粒的不确定性度量及其关系进行了研究；文献［6-7］利用条件熵度量开发了启发约简算法；文献［8］研究了知识积分与知识熵之间的关系；文献［9］在粗糙集中对互信息进行了研究，为不确定性度量提供了更新的粒计算解释；文献［10］在粗糙集理论中定义了一种新的信息熵——互补熵，考虑了信息函数补的性质；文献［11-12］在粗糙集中定义组合熵并研究了其性质；文献［13］介绍了几种熵在不完备信息系统中的应用；文献［14］基于三层粒结构定义了三支信息度量；文献［15］基于三层粒结构定义了三支单调邻域熵.

综上多种信息度量，可见粗糙熵是较早引进的度量，其直接模拟表达具有意义，但相关研究还欠缺.本文将通过粗糙熵［4］的表达公式，结合三支概率，先定义三支变形熵，因其中有一支无粒化单调性，进而定义三支加权变形熵，并证明它的单调性与系统性.三支加权变形熵推进了粗糙熵的发展，有益于粗糙集不确定性的表示及应用.

1 预备知识

本章通过文献［14］和［4］简要介绍决策表与粗糙熵.

粗糙集的基本数据是以下信息表：

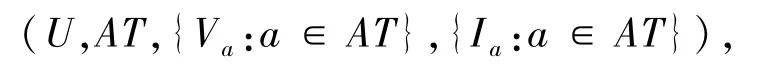
其中，U是一个非空的有限论域，AT是非空的有限属性集，Va是值域，对∀a∈AT，Ia：U→Va是一个信息函数.每个对象x在属性a下有属性值Ia（x）.特别地，决策表是一种特殊类型的信息表，其中AT＝C∪D，C∩D＝Ø，C和D分别代表条件属性集和决策属性集.

为了方便，决策表被记作（U，C∪D）.在属性约简中，条件属性涉及子集参数A⊆C，而决策表属性涉及常数D.属性集A的等价关系被定义为：

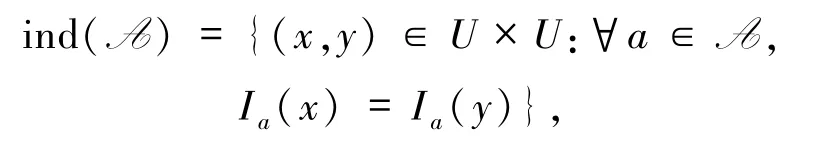
其诱导等价类［x］A，这是一种基本粒.分类结构

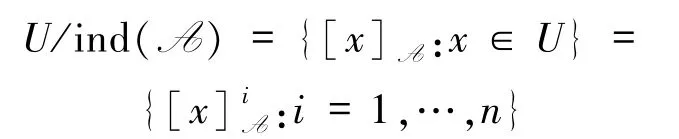
称为知识分类或条件分类，其中｜U／ind（A）｜＝n.类似地，D可以导出等价关系ind（D）和进一步的决策分类

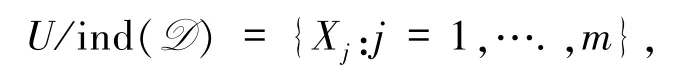
后者由m个决策类组成，即｜U／ind（D）｜＝m.

对于决策表（U，C∪D），文献［14］提供了三层粒结构：

1）宏观高层包括条件分类U／ind（A）和决策分类U／ind（D），以展现宏观规模和高层级水平；

2）中观中层包括条件分类U／ind（A）和决策类Xj，以体现中观规模和中层级水平；

粗糙集理论（特别是其属性约简）涉及的不确定性主要关联于知识粒化（即条件分类粒化）.设B⊆A⊆C，则 U／ind（A）与 U／ind（B）分别对应着较细与较粗的粒度结构，它们确定着一种偏序转化，相关的粒度粗化表示为

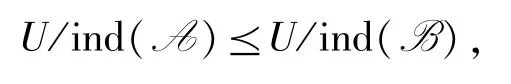
对应有

即知识粗化蕴含着一些粒合并的组.在粗糙集理论及其属性约简中，知识粒化提供了表象不确定性的粒计算机制，而粒化单调性则成为评估不确定性度量的基本准则.可见，对粒化单调性的研究很有必要.特别地，文献［16］指出粒化单调性只需证其中的一组粒合并.

定义1［14］先验概率、后验概率、似然概率分别定义如下：

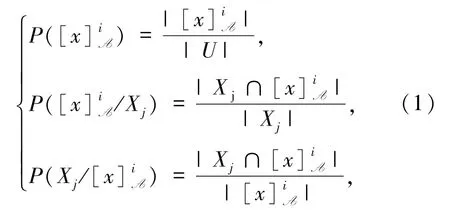
它们统称为三支概率.

定理1［14］三支概率服从如下贝叶斯定理：

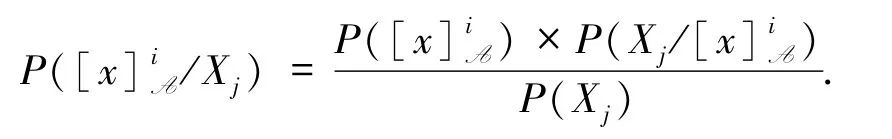
因为三支概率分别对应相对和绝对度量，所以具有不同的概率语义和决策行为.特别地和分别直接地“从因到果”和“从果到因”地直接反映因果关系.因此，它们的相关融合可以很好地描述决策概念与条件结构之间的相互关系.而贝叶斯定理表达了三支概率的系统性，为深入的不确定度量构建奠定了基础.

定义 2粗糙熵 E（A）定义为［4］：

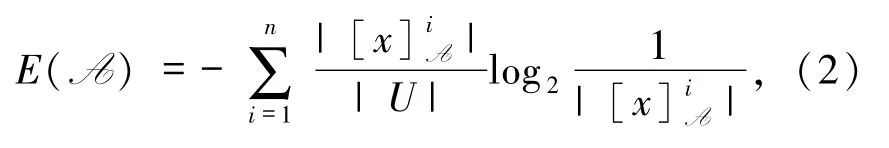
其具有相等的概率表示：

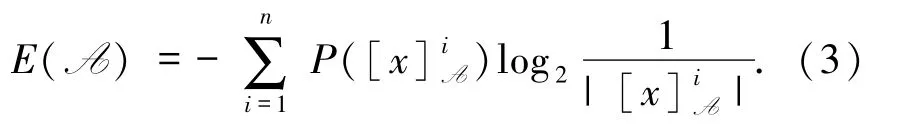
2 三支变形熵

本节模仿粗糙熵，考虑三支概率定义三支变形熵，并聚焦其中的粒化单调性.

定义3三支变形熵定义为：

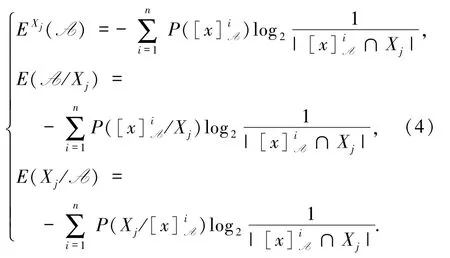
基于三支概率构建的三支变形熵，具有三支概率的特征.EXj（A）偏向绝对评估，而 E（A／Xj）和E（Xj／A）从两个不同的因果方向做交互描述.因此，三支变形熵（尤其是 E（A／Xj）和 E（Xj／A））能够度量条件分类U／ind（A）和决策类Xj之间的因果关系.接下来，讨论三支变形熵的粒化单调性.

命题 3EXj（A）和 E（A／Xj）具有粒化单调性：

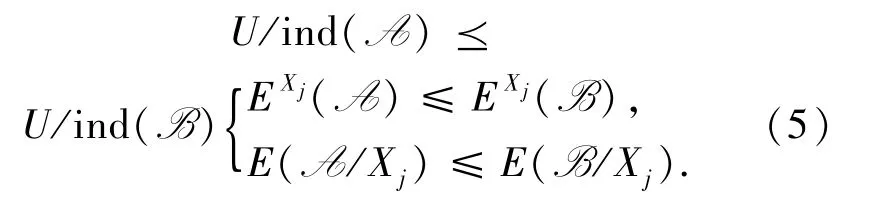
证明1）于粒合并代表组有

2）利用同样于1）的方法可以推出，当

时，E（A／Xj）≤E（B／Xj）成立.

此外，E（Xj／A）只有粒化非单调性，该结果可由下面的一个例子来验证.总之，三支变形熵只有其中两支有粒化单调性，有一支非粒化单调，故三支变形熵具有改进空间.

例 1给定决策表（U，C∪D），其中 U＝｛x1，x2，…，x80｝具有 80 个元素，C＝｛a，b，c｝具有 3 个条件属性，D＝｛d｝具有1个决策属性.相关数据见表1，下面提供一个统计说明.

1）对于前 40 个元素x1，x2，…，x40，它们在属性a下的值全为 1；在 b、c下的值全为 -1；除了Id（x1）＝1，后面的39个元在 d下的值全为0.

2）对于后40 个元素x41，x42，…，x80，它们在属性 a下的值全为0；除了Ib（x1）＝1，后面的39个元在 b下的值均为0；除了Ic（x80）＝1，前面的39个元在c下的值全为0；前29个元在d下的值为1，而后11个元在d下的值取0.

下面，设Xj为d值取1的所有30个元素之集，即 Xj＝｛x：Id（x）＝1｝＝｛x1，x41，…，x69｝，｜Xj｜＝30，并设 B＝｛a｝，则

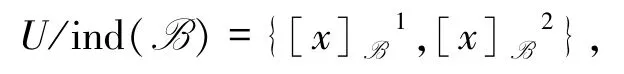
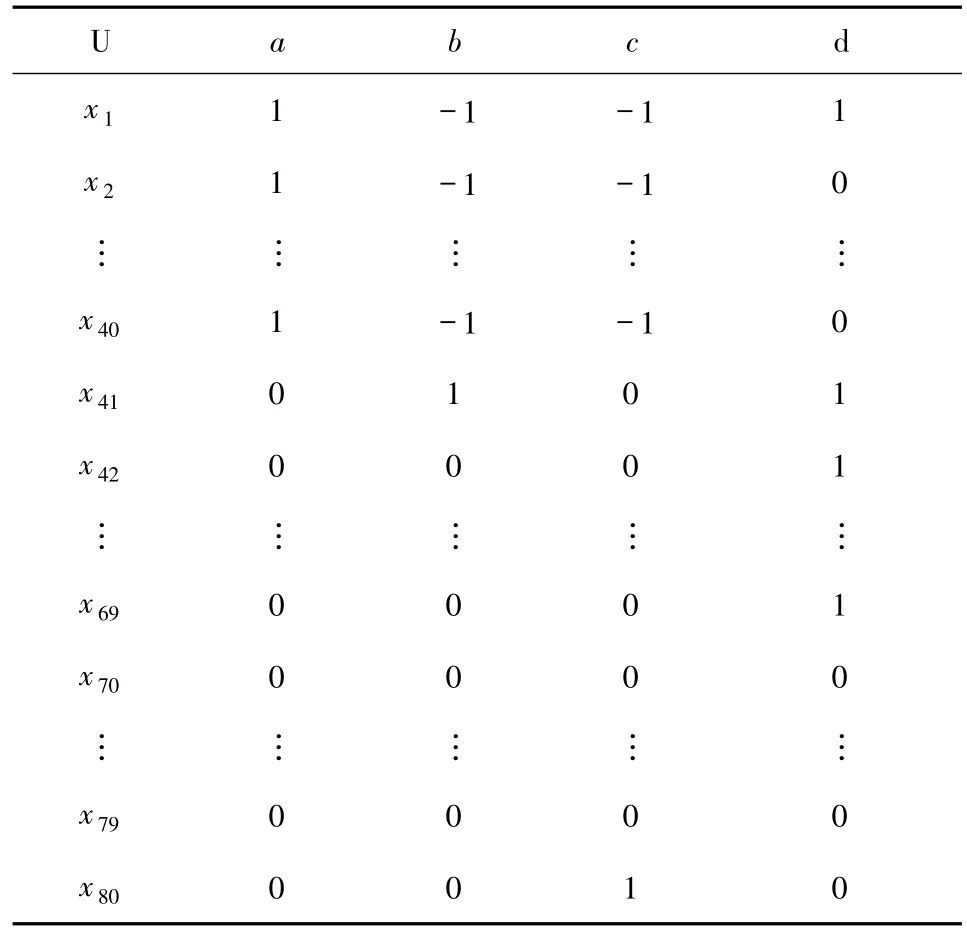
表1 实例的决策表Tab.1 Decision table of the example

可知

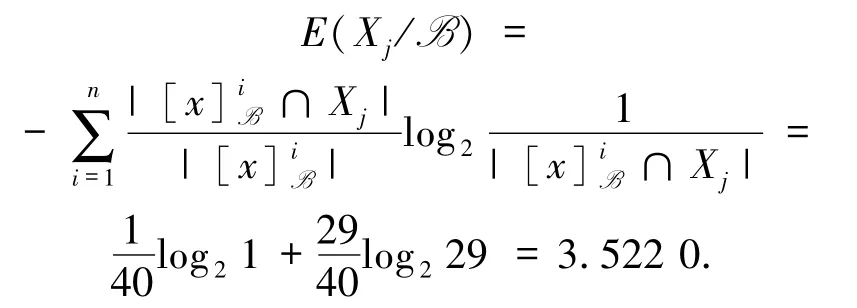
1）若设 A＝｛a，b｝，则

因

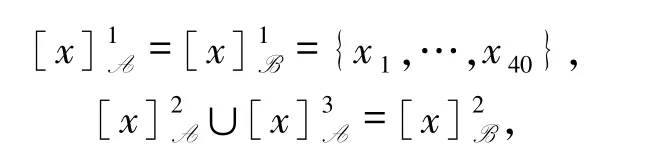
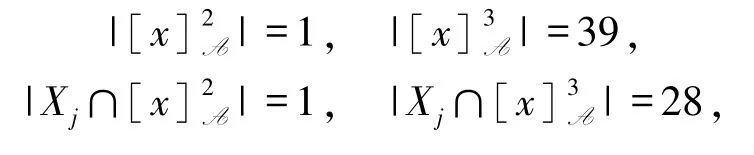
则

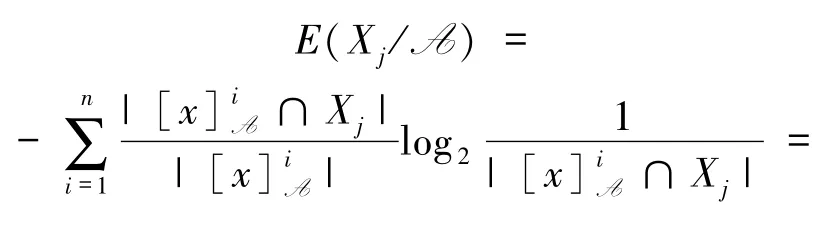
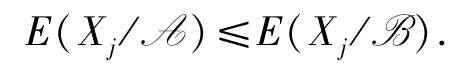
2）若设 A＝｛a，c｝，则

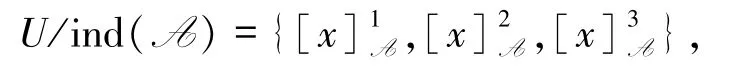
因

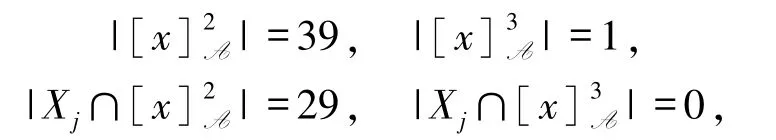
则

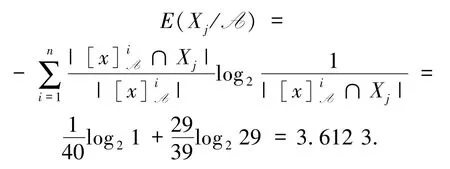
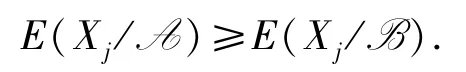
综上，E（Xj／A）不具有粒化单调性的性质.

3 三支加权变形熵

由上，三支变形熵有一支具有非粒化单调性；另外，系统性也缺损.为此，本节构建三支加权变形熵，以进行相关改进.根据贝叶斯公式，三支概率具有良好的系统性.本节将以贝叶斯公式为起点，对贝叶斯公式进行变换，进而构建三支加权变形熵.

由贝叶斯公式有：

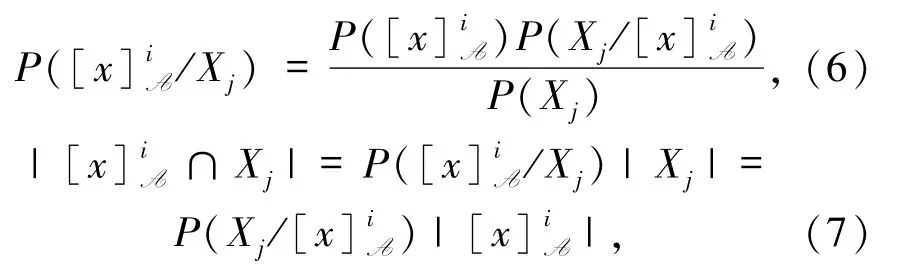
由（8）和（9）式两边对应相加得

再基于i的累加有

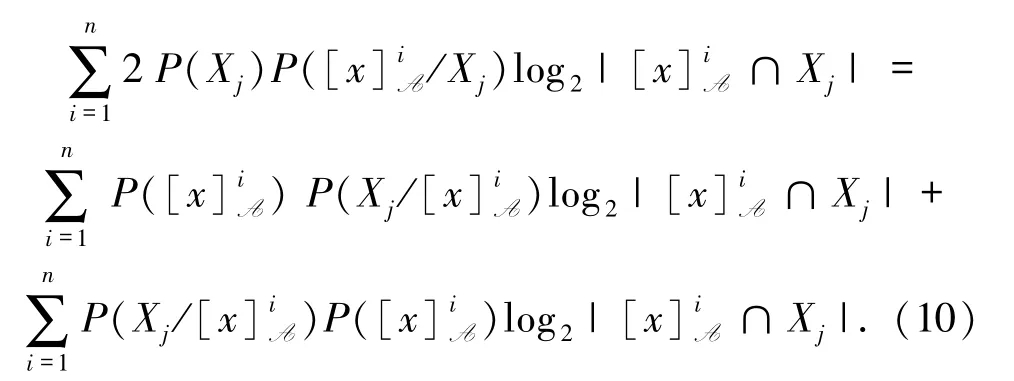
基于（10）式，由三支概率的不确定性语义，将三支变形熵与相应具体概率的权重系数融合，进而得到三支加权变形熵.

定义4三支加权变形熵定义为：

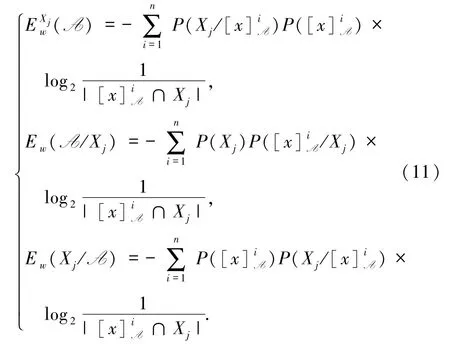
推论1

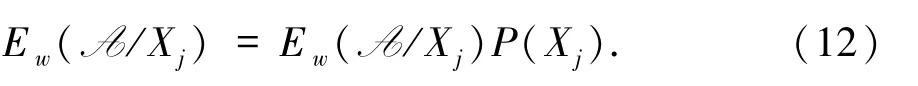
定理3三支加权变形熵具有系统性

根据（11）式，三支加权变形熵将概率权重引入三支变形熵中，用来反映信息的重要性或关注度.三支加权变形熵的权函数分别为

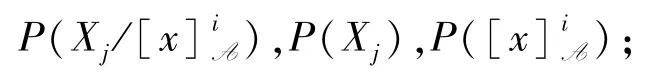
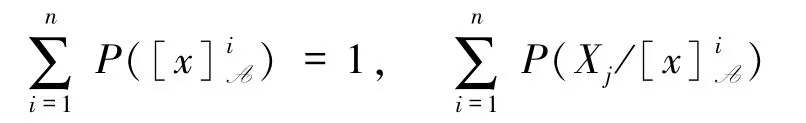
不确定.这里，加权主要基于系数来称谓，其意义比“权和为1”的一般加权更广泛.三支加权变形熵不仅起着重要的作用，并可以建立起系统方程.实质上，当采用三支加权变形熵时，用到了双量化融合思想，以便获得更好的信息特征.接下来，将阐述三支加权变形熵的粒化单调性.

定理4三支加权变形熵具有粒化单调性：

证明因三支变形熵E（A／Xj）具有粒化单调性，而 P（Xj）为常数，故 EW（A／Xj）≤EW（B／Xj）显然成立.对此，下面只证明不等式

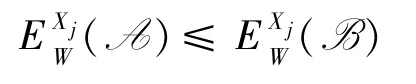
和

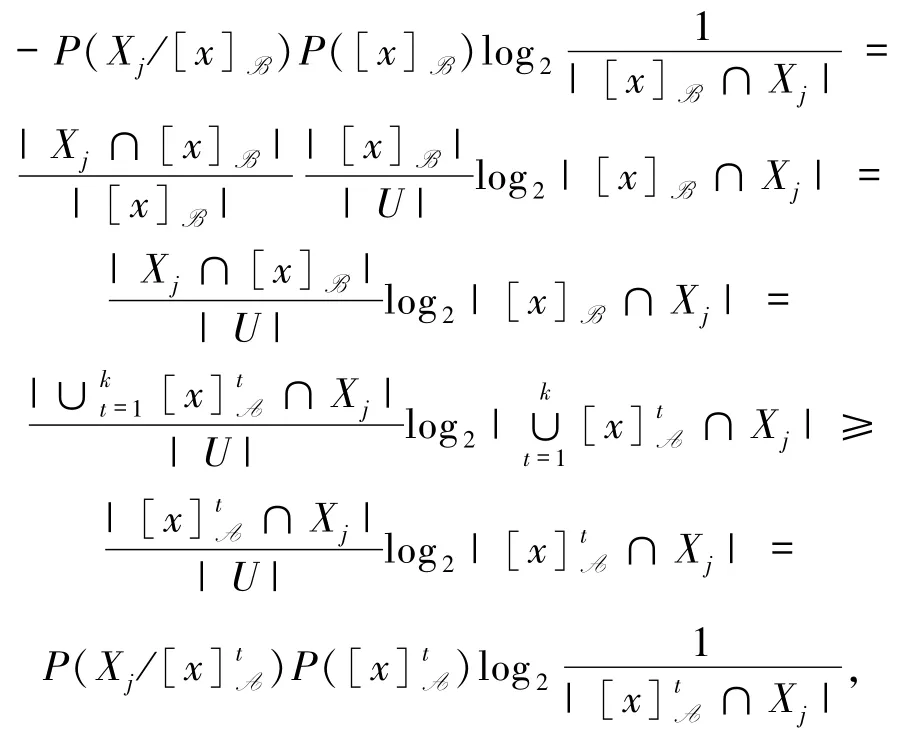
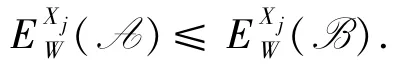
有

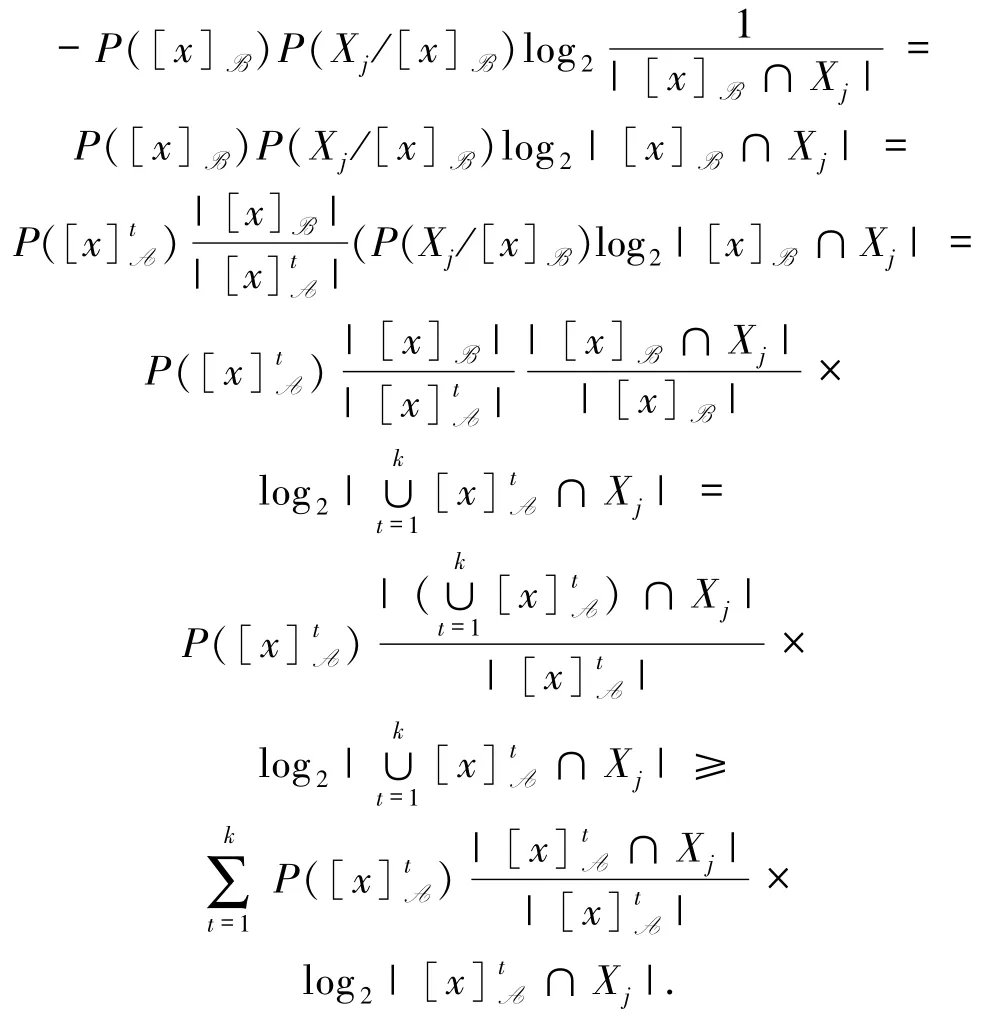
本节基于微观底层的三支概率和贝叶斯公式，构造了三支加权变形熵，并讨论和证明了它的系统性和粒化单调性，可以更好地描述关于条件分类U／ind（A）和决策类Xj的系统，并改进了前面的三支变形熵.

4 结论

粗糙熵［3］由来已久，其相关研究具有意义.本文借鉴粗糙熵，结合三支概率定义了三支变形熵和三支加权变形熵，深入地诠释了粗糙集中的不确定性度量，丰富了粒计算和三支决策，为不确定度量提供了更为完整和更新的粒计算解释.从决策表的三层粒度［14］结构来看，本文主要立足于中观中层，后续宏观高层的构建还需要讨论.此外，后续相关的不确定性应用，如属性约简还值得深入讨论.