基于Hydrus-2D的红壤区涌泉根灌自由入渗土壤水分运移数值模拟
代智光
(南昌工程学院水利与生态工程学院,江西 南昌 330099)
红壤主要分布在我国南方丘陵区,是我国主要土壤资源之一。红壤区光热资源充足,气候条件优越,特别适合柑、橘等果树的生长。随着农业的发展,红壤区季节性干旱以及红壤酸黏贫瘠等问题日益突出,人们往往通过过量灌溉来提高果树产量,这不仅导致灌溉水利用效率低下,而且造成当地土壤侵蚀和养分流失问题突出,发展科学合理的灌溉技术迫在眉睫。
涌泉根灌是一种微灌新技术,类似于地下滴灌,它通过埋在地下的灌水器将水分直接输送到作物根区进行局部灌溉,提高了水分利用效率。相比其它灌溉方式,涌泉根灌出流方式为三维柱状出流,与土壤接触面积大,特别适宜于红壤等质地较为黏重的土壤。近些年,相关学者对涌泉根灌技术进行了大量研究,如Dai等[1-2]通过枣树的涌泉根灌水氮耦合试验研究表明,涌泉根灌能有效提高果树的水肥利用效率,特别适宜于果树灌溉;刘风华等[3]研究了容重对红壤区涌泉根灌土壤水分的运移特性影响,结果表明容重不同土壤水分运移特性存在显著差异;代智光等[4]研究肥液浓度对红壤区涌泉根灌水氮运移特性的影响,并建立了土壤累计入渗量及湿润锋运移距离与肥液浓度的关系模型;费良军等[5]研究了黄土高原地区不同肥液浓度对涌泉根灌土壤湿润体的影响,揭示了涌泉根灌土壤入渗量和湿润锋运移距离随肥液浓度的变化关系;吴恒卿等[6]对双点源涌泉根灌交汇入渗土壤湿润体特性进行了试验研究,结果表明灌水器间距对湿润体的运移、交汇时间、土壤含水率有明显影响。近些年,国内外对土壤水分运移的数值模拟开展了大量研究工作,如美国盐分实验室开发的Hydrus1D/2D/3D软件可以模拟饱和非饱和土壤水、热、盐、单组分和多组分溶质运移转化问题;李耀刚等[7]采用Hydrus-3D软件模拟了陕北黄绵土涌泉根灌土壤水分的运移,结果较好;Kandelous等[8]利用Hydrus-2D软件对地下滴灌的土壤水和溶质运移进行了模拟,精度满足要求;Cai等[9]利用Hydrus-2D软件对陶瓷根灌土壤水分运移进行了模拟,结果满足要求;李久生等[10]基于土壤水分运动的动力学方程和溶质运移的对流-弥散方程,建立了不同土壤中地表滴灌水肥运移的Hydrus-2D模型,并对模型进行了求解;赵新宇等[11]采用Hydrus-3D软件对涌泉灌的水分运移进行了模拟,结果较好。
目前,有关红壤区涌泉根灌土壤水分运移的研究还主要集中在室内试验,局限性较强,而对土壤水分运移的模拟研究还少见报道。基于此,本文通过红壤区涌泉根灌土壤水分运动的数值模拟,并与室内试验结果相对比,验证Hydrus软件在红壤区涌泉根灌中的适用性,以期为涌泉根灌技术在红壤区的推广应用提供参考。
1 材料与方法
1.1 试验土壤
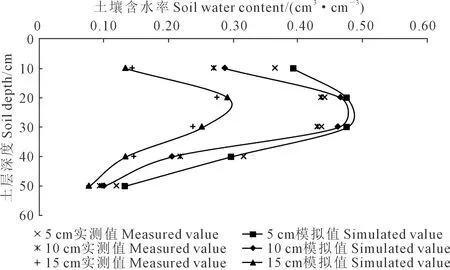
试验于2019年5月在南昌工程学院灌溉排水实验室进行,供试土壤取自江西省进贤县田间表层0~50 cm熟土,土壤经自然风干后进行研磨,过2 mm筛备用。土壤颗粒组成用激光粒度分析仪(MS2000型,马尔文,英国)测定,粒径为0 mm 试验装置主要由马氏瓶、土箱和灌水器组成(图1)。马氏瓶用于提供恒定水头,其内径为14 cm,高为100 cm,通过调整出口开关来控制出流流量;土箱材质为有机玻璃,长×宽×高为50 cm×50 cm×50 cm;灌水器长度为20 cm,内径为4 cm,在其下部10 cm范围内均匀开孔,开孔率为25%,取1/4用玻璃胶粘于土箱一角,并用纱布包裹以避免土壤颗粒堵塞灌水器。试验土壤初始含水率为10.20%(体积含水率),设定土壤容重为1.35 g·cm-3,灌水历时180 min。灌水器初始流量设2个梯度:2.0、3.0 L·h-1,其中2.0 L·h-1用于参数率定,3.0 L·h-1用于模型验证。 1.马氏瓶 Markow bottle; 2.橡胶管 Rubber tube; 3. 土箱 Test box;4. 湿润体 Wet body; 5. 灌水器细部 Detail of emitter 图1 试验装置示意图及灌水器细部Fig.1 Schematic diagram of the test device anddetails of the irrigator 将试验土壤按容重分层(每层5 cm)装入土箱,层间打毛,自然沉降24 h后开始试验,按先密后疏的原则设定时间间隔,观测马氏瓶读数,同时以灌水器底部为起点,用直尺测量湿润锋在竖直向上、竖直向下和水平方向的运移距离。试验结束时,在距离灌水器5、10、15 cm处使用土钻取土,每隔10 cm 取样1次,取土深度为50 cm。每组试验重复3次,取其平均值。 涌泉根灌土壤水分入渗为三维柱状水分入渗。假定土壤各向同性,则土壤水分为轴对称分布,因此本文选用Hydrus-2D模型进行模拟研究。本次室内试验时长为180 min,由于试验时间较短,因此地表蒸发可忽略。不考虑空气、温度及滞后效应对土壤水分的影响,则土壤水分运动用Richards方程描述为: (1) 式中,θ为土壤体积含水率(cm3·cm-3);t为入渗历时(min);K(h)为非饱和导水率(cm·min-1);h为土壤水头(cm);x,z为坐标轴,其中z轴向上为正(cm)。 2.2.1 初始条件 土壤水分运动方程的初始条件为: h(x,y,z,t)=h0(x,y,z) (2) 式中,h0(x,y,z)为土壤初始负压水头(cm);X,Z为模拟计算区域横向和竖向的最大长度,与室内试验土箱一致,即X=Z=50 cm。 图2 数值模拟控制体Fig.2 Numerical simulation control body 2.2.2 边界条件 图1为涌泉根灌土壤水分运动数值模拟控制体示意图,O点为坐标系原点。由于室内试验不考虑蒸发,因此上边界DE段:∂h/∂z=0 (2 cm≤x≤50 cm,z=50 cm,t>0 min);右边界为土箱边壁,因此EF为零通量面,即∂h/∂z=0 (x=50 cm,0 cm≤z≤50 cm,t>0 min);下边界为土箱底部,因此FO也为零通量面,即∂h/∂x=0 (0 cm≤x≤50 cm,z=0 cm,t>0 min);左边界OA段为土箱边壁,则有∂h/∂z=0 (x=0,0 cm≤z≤30 cm,t>0 min);CD段为灌水器迷宫流道部分,因此∂h/∂z=0 (x=2 cm,40 cm≤z≤50 cm,t>0 min)。 AB和BC段为灌水器出流部分,由于涌泉根灌流量较大,灌水器出流量大于土壤入渗量,因此套管中形成积水,积水深度随着时间不断变化,开始阶段逐渐增加,一定时间后达到稳定,因此按变水头边界处理:h(x,y,z,t)=H(0 cm≤x≤2 cm,z=30 cm,t>0 min;x=2 cm,30 cm≤z≤40 cm,t>0 min),其中H为灌水器内积水深度,通过试验过程中实测可得。 利用Galerkin有限单元法完成对数学模型的数值计算,时间采用隐式差分法离散[13-14]。计算区内网格划分采用三角形单元,网格尺寸划分见图2,三角形边长为3 cm,灌水器位置入渗界面处适当加密网格,以提高计算精度。 在Hydrus-2D模型中,土壤水分特征曲线采用Van Genuchten (VG)模型,其表达式为: (3) 式中,θ(h)为土壤体积含水率,与土壤水吸力有关(cm3·cm-3);θr为土壤滞留含水率(cm3·cm-3);θs为土壤饱和含水率(cm3·cm-3);h为土壤吸力(cm),当土壤处于饱和状态时,h=0;α为土壤尺度函数,其值为土壤进气吸力值的倒数(cm-1),容重较大的土壤,其对应的进气吸力值较大,而土壤容重较小时,对应的进气吸力值也较小;参数n与土壤水分特征曲线的坡度有关,对于砂质土而言,其土壤特征曲线的坡度较缓,对应的参数n就较大,对于粘性土壤而言,其土壤特征曲线的坡度较陡,其对应的参数值n就较小;参数m=1-1/n(n>1)。 土壤非饱和导水率公式为: K(θ)=Ks×S0.5[1-(1-S1/m)m]2 (4) (5) 式中,S为饱和度;Ks为饱和导水率(cm·min-1)。θs、θr、Ks通过室内试验测定。利用RETC软件获取土壤水分特征曲线初始参数α、n,采用马氏瓶流量为2.0 L·h-1时的实测数据进行率定。 运行模型并在一定范围内调整参数,使模拟值尽可能接近实测值(表1)。利用SPSS 21.0软件对湿润锋运移距离及不同时刻含水率的模拟值和实测值分别进行对比,当决定系数(R2)均大于0.05水平对应的临界决定系数,土壤湿润锋和含水率的均方根误差分别小于1.5 cm和0.05 cm3·cm-3、F检验P值>0.05时,认为精度满足要求,确定模型参数。 图3为涌泉根灌自由入渗实测和模拟对比。土壤各向湿润锋运移距离的模拟值和实测值随入渗历时变化见图4。由图4可知,在灌水结束时,土壤各向湿润锋运移距离的模拟值和实测值基本一致,均表现为随着入渗历时的增长先快速增加,而后缓慢增加的变化趋势,这是因为在开始阶段土壤含水率还较低,土壤空气含量较高,因此水分运移速度也较快,随着入渗历时的逐渐增长,土壤空气含量逐渐减小,因此土壤水分运移速度也逐渐变慢。 在灌水结束时,在竖直向上方向湿润锋均达到土箱表层;在竖直向下方向模拟值和实测值分别为22.2、21.1 cm,相差1.1 cm,相对误差均为5.21%;在水平方向,模拟值和实测值分别为19.1、20.6 cm,相对误差仅为-7.28%,可以看出,在灌水结束时,各向湿润锋的相对误差均不超过±10%。 图5为灌水结束时,距离灌水器5、10、15 cm处土壤水分在0~50 cm土层内的分布。可以看出,在灌水结束时,距离灌水器不同距离处土壤含水率剖面分布的模拟值和实测值基本一致,均表现为随着土层深度的增加而先增大后减小,这是因为灌水器埋置于20 cm处,距离灌水器越近,土壤水分就越容易到达,因此相应的土壤含水率就越大。 图3 涌泉根灌自由入渗实测和模拟对比Fig.3 Comparison of measured and simulated of freeinfiltration of surge-root irrigation 表2 湿润锋运移距离模拟误差分析 通过对模拟误差的分析表明,在距离灌水器5 cm处,40~50 cm土层的模拟误差最大,其值为9.92%;在距离灌水器10 cm处,20~30 cm土层的模拟误差最大,其值为7.39%;在距离灌水器15 cm处,30~40 cm土层的模拟误差最大,其值为-8.37%,可以看出在距离灌水器不同位置处,误差的分布比较随机,且均在±10%以内。 图5 距离灌水器不同距离处土壤含水率模拟值和实测值对比Fig.5 Comparison of simulated and measured values of soilwater content at different distances from the irrigator 表3 土壤含水率模拟误差分析 根据土壤水动力学理论结合土壤水分的运动特征,建立了红壤区涌泉根灌条件下土壤水分运动的数学模型,按照试验条件设定数值模拟边界条件,并采用Hydrus-2D软件对所建模型进行求解。通过涌泉根灌土壤水分随时间的变化规律及空间分布规律的模拟值与实测值的对比可知,土壤湿润锋运移距离和土壤含水率随时间变化的模拟值与实测值非常吻合,相对误差均在±10%以内,湿润锋运移距离和含水率模拟值和实测值之间RMSE分别小于1.300 cm和0.030 cm3·cm-3,且差异均未达到显著水平,这说明Hydrus-2D软件可以用于红壤区涌泉根灌土壤水分运动的模拟。1.2 试验装置及试验设计

2 数学模型
2.1 土壤水分运动基本方程
2.2 定解条件
0≤x≤X,0≤z≤Z,t=0
2.3 数值求解方法
2.4 模型参数率定
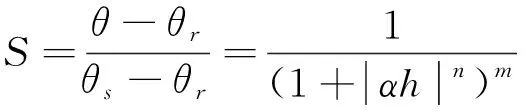
3 模型准确性评价
3.1 湿润锋运移距离模拟准确性评价

3.2 土壤剖面含水率模拟准确性评价




4 结 论

