BDS-3时间频率传递方法及其性能分析

张鹏飞，涂 锐，广 伟，卢晓春

(1.中国科学院国家授时中心，西安 710600；2.中国科学院时间频率基准重点实验室,西安 710600；3.中国科学院精密导航定位与定时技术重点实验室,西安 710600；4.中国科学院大学，北京 100049)

0 引言

高精度的时间传递是时间实验室的重要工作之一。相对于卫星双向和光纤等专用技术手段，全球导航卫星系统(Global Navigation Satellite System，GNSS)技术具有设备成本低、维护简单、测量精度高等特点，已逐渐成为国际时间传递工作中的重要技术手段。其实施方法也从早期的共视法时间传递，发展到了全视法时间传递，特别是基于载波相位观测值的时间传递方法，国内外学者对其关键技术问题进行了深入研究和分析。早在1980年，Allan和Weiss利用全球定位系统(Global Positioning System，GPS)共视法实现了远程时间传递，获得了ns量级的时间传递精度。2003年，Ray等学者指出基于GPS载波相位时间传递技术获得的链路钟差序列中存在明显的天跳变不连续现象[1-2]。2007年Petit和Jiang利用GPS 精密单点定位(Precise Point Positioning，PPP)技术进行了精密时间传递的研究，认为其精度可以达到亚ns量级[3]。Defraigne和Jiang等学者通过实验分析了融合GPS和GLONASS的远程时间传递方法，认为联合双系统的时间传递方法有助于进一步提升时间传递的性能[4-6]。随着我国BDS-2卫星导航系统的不断建设和完善，Guang和Liang等学者将BDS-2应用于国际时间传递的工作中，进一步拓展了北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)在时间传递工作中的应用[7-8]。国内方面，聂桂根较早地指出了利用GPS载波相位技术进行时间传递的理论精度可达0.1ns[9]。张小红等利用静态PPP技术分析了不同时间间隔的精密卫星钟差产品进行单站时间传递的性能，从短期和长期2个角度对比分析了其频率稳定度[10]。黄观文通过研究GPS载波相位时间传递中的天跳变现象，提出了一种基于参数先验贝叶斯估计的连续时频传递算法来削弱其影响[11]。2016年，于合理提出了一种附加原子钟物理模型的PPP时间传递算法，显著提升了时间传递的精度和稳定性[12]。孙清峰等通过实验对比分析了融合GPS/BDS/GLONASS/Galileo这4个系统的PPP技术，可以实现亚ns级的时间传递，其精度较GPS单系统具有一定程度的提高[13]。张鹏飞等对基于BDS-2的时间传递性能进行了深入分析[14]，同时系统地研究了BDS-2伪距系统偏差对精密时间传递的影响以及解决策略[15]。涂锐等首次提出了BDS非差非组合观测值的时间传递模型，并与常规模型进行了比较分析，得到了一致的结果[16]。

上述学者的深入研究极大地推动了GNSS时间传递技术的发展，但是前期研究主要集中在GPS和GLONASS等方面，对于当前新兴的BDS-3全球系统的研究相对较少。BDS是由我国自主研发、能够独立运行的全球卫星导航系统，计划在2020年完成全球覆盖的建设目标[17]。考虑到BDS-3卫星在卫星载荷和信号设计等方面与BDS-2区域系统有显著不同，其应用于远程时间精密传递的性能有待进一步分析。因此，本文选取了2个国际时间实验室的BDS-3观测数据，建立了2条不同长度的时间传递链路，从定性和定量方面分析了BDS-3时间传递的性能。

1 BDS-3时间传递方法

1.1 共视法时间传递

GNSS共视法(Common View，CV)是目前远程时间比对的主要方式之一。其基本原理是位于两地的用户接收机在同一时刻同时观测同一颗卫星，以消除或削弱卫星星历及钟误差，以及卫星信号传播路径上的部分公共误差，实现两地的时间传递。假设A地本地时钟的时间为τa，B地本地时钟的时间为τb，卫星钟的时间为τs，于是，位于两地的时钟相对于卫星钟的时间分别为

τas=τa-τs-τaΔ

(1)

τbs=τb-τs-τbΔ

(2)

式中，τaΔ与τbΔ分别为两站到卫星传播路径上的延迟。于是，两站之间的时差即可表示为

τab=τas-τbs-(τaΔ-τbΔ)

(3)

若两站之间的距离较近时，共视法利用其较强的相关性能够很好地消除或者削弱信号传播路径上的误差。随着距离的增大，两站间的误差的相关性也逐渐减弱，共视比对精度将会逐渐降低。

近年来，随着共视法在时间传递中的广泛应用，国际上已逐步形成了其数据处理流程规范GNSS通用时间传递标准版本(Common GNSS Generic Time Transfer Standard Version 2E，CGGTTS V2E)，即：各个测站以16min作为共视时段单元，首先连续跟踪卫星13min；然后将其分成52组，每组15个点，对52组使用二次多项式拟合选取中点处的值；最后将这52个数据线性拟合，取中点处的值为最终参加实际计算的伪距观测值[14]。通过上述处理方式对伪距的观测噪声予以改善，最终利用式(3)即可获得两地时间传递量UTC(A)-UTC(B)。GNSS共视法时间传递示意图如图1所示。

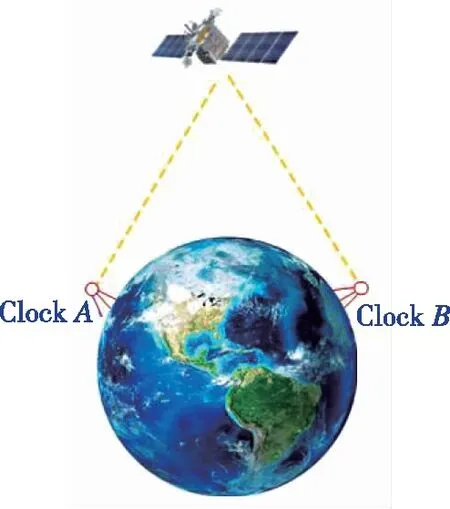
图1 GNSS共视法时间传递示意图Fig.1 Schematic diagram of GNSS common view time transfer

1.2 载波相位法时间传递

GNSS载波相位法(Carrier Phase，CP)主要是利用了伪距观测值中时间信息和载波相位观测值的低噪声优势，从原理上提升时间传递精度。其数学模型采用了双频伪距和载波相位观测值，构建无电离层组合模型，以消除一阶电离层延迟的影响，并利用其组建观测方程[18]

(4)

式中，ρ为卫星与地面站间的距离；dtr表示接收机钟差；dts表示卫星钟差；dtrop表示对流层延迟；λ为一阶无电离层组合后观测量的波长；c为光在真空中的速度；N为模糊度参数;ε(PIF)与ε(ΦIF)分别为伪距和相位观测值无电离层组合后的观测量噪声;PIF和LIF分别为伪距和载波相位的无电离层组合观测量。

将式(4)进行线性化和进一步转化，其待估未知参量可以写为

X=(x,y,z,dtr,dtrop,N)T

(5)

式中，(x,y,z)为测站位置参数，dtrop为对流层延迟估计参数，N为模糊度参数。如图2所示，在数据处理中，载波相位时间传递法的两站不需要同时观测同一颗卫星，采用国际GNSS服务组织(International GNSS Service，IGS)提供的精密轨道和钟差产品将本地钟统一参考于IGST(time scale of IGS)，即接收机钟差dtr代表接收机外接原子钟时间频率标准与IGST之间的钟差，即

dtr(a)=τ(a)-IGST

(6)

dtr(b)=τ(b)-IGST

(7)

于是，两地之间的时间传递量可进一步表示为

τab=dtr(a)-dtr(b)

(8)

图2 GNSS载波相位法时间传递示意图Fig.2 Schematic diagram of GNSS carrier phase time transfer

需要说明的是，不论共视法还是载波相位法时间传递，在测站获取GNSS卫星信号的过程中用到的GNSS接收机、天线，以及各种线缆均会引起一定量的硬件延迟，需要通过不同的校准方法进行准确测量[19]。

2 时间传递实验与精度分析

2.1 实验数据

为了充分验证分析BDS-3时间传递的性能，本文主要围绕时间传递的共视法和载波相位法两种主要技术手段，选取了位于德国联邦物理技术研究院(Physikalisch-Technische Bundesanstalt，PTB)的国际GNSS监测评估系统(International GNSS Monitoring and Assessment System，iGMAS)站BRCH, 其外接时间频率为该机构建立和维持的UTC(PTB)，同时该时间频率参考也是国际时间传递中的节点。由于在时间传递过程中，位于链路两端的时频参考也在实时变化，无法采用其他更高精度的技术手段进行反复测量获取一种外符合参考，因此在实验设计中，本文选取了位于捷克科学院的TP01和TP02站，两站均连接有相同频率源UTC(TP)。另外，考虑到各站的BDS-3接收机有不同的观测天线和接收机硬件，相关线缆也不相同，钟差传递量则包含这些硬件延迟之差，在一定的时间内，这些时间延迟相对平稳，有利于进行性能分析。

考虑所选择的3个测站不仅能够跟踪到BDS-3的卫星信号，还能接收BDS-2的数据，因此，在本文的时间传递实验中，分别对位于2条时间传递链路(BRCH-TP01)和(TP02-TP01)上的BDS-2和BDS-3数据进行对比分析。其中BRCH-TP01为长基线，基线距离为368.3km；TP02-TP01为共钟短基线，基线距离为4.6m。实验时间段为2020年2月3日～2月4日，基于课题组自主开发的GNSS远程时间传递软件(PPTSlo)分别对各站接收机的钟差进行估计，共视法的卫星星历采用广播星历，载波相位法采用德国地学研究中心(GFZ)提供的GBM多模精密卫星轨道及钟差产品。

2.2 共视法时间传递结果

图3给出了基于BDS-2和BDS-3共视法在BRCH-TP01链路上的钟差序列。从图3中可以看出，BDS-2和BDS-3的钟差序列存在明显的系统性偏差，这主要是由于不同系统的延迟并不一致，在链路校准中可对其进行准确的标定。另外，从图3中还可以明显地看出，BDS-3钟差序列的连续性明显优于BDS-2，究其原因主要是BRCH和TP01站位于欧洲地区，BDS-2作为区域卫星导航系统，在此区域可见卫星数较少，而BDS-3是全球系统，其可见卫星数目相对较多。最后，BDS-3链路钟差的噪声水平显著小于BDS-2，为了定量对其进行分析。本文选用时间传递中常用的Vondark方法对求解的钟差序列进行平滑，BDS-2和BDS-3平滑残差的均方根(Root Mean Square，RMS)值分别为3.13ns和1.48ns。

图3 基于共视法获取的BRCH-TP01链路钟差序列Fig.3 Clock difference sequence of BRCH-TP01 link based on common view method

图4给出了BDS-2和BDS-3共视法在TP02-TP01链路上的钟差序列。由于此链路为共钟链路，其时间传递量的变化在很大程度是链路上所使用到的硬件延迟的变化量。其链路钟差的变化在整个时间传递实验中明显小于BRCH-TP01链路。同样地，BDS-3的噪声水平也明显小于BDS-2，其平滑残差的RMS分别为0.65ns(BDS-3)和1.02ns(BDS-2)。

图4 基于共视法获取的TP02-TP01链路钟差序列Fig.4 Clock difference sequence of TP02-TP01 link based on common view method

在时频领域中，链路的钟差序列由于包含了两个时间频率参考的物理信号，导致其序列是非平稳特征。对于这类数据的评价，其均值和标准差不会收敛到某个值，当增加测量次数时，平均值也会滑动地改变，标准差也会随之增大。显然，用标准差来描述频率标准的稳定度是不合适的。为了解决这一问题，世界各国学者提出了各种频率标准时域频率稳定度的表征方法，目前采用最多的是由美国学者D. W. Allan提出的表征方法，即所谓的Allan方差来反映其频率稳定度。图5和图6分别表示了共视法获取的BRCH-TP01和TP02-TP01链路的Allan方差。从图中可以看出，在2条时间传递链路上，BDS-3与BDS-2的Allan方差规律也较为一致;另一方面，在不同的时间间隔上，BDS-3明显优于BDS-2方案，万秒稳定度能达到10-13量级。

图5 共视法获取的BRCH-TP01链路的Allan方差Fig.5 Allan variance of BRCH-TP01 link by common view method

图6 共视法获取的TP02-TP01链路的Allan方差Fig.6 Allan variance of TP02-TP01 link by common view method

2.3 载波相位法时间传递结果

图7和图8分别给出了载波相位法获得的BRCH-TP01和TP02-TP01链路的时间传递钟差序列。从图中可以看出，BDS-2与BDS-3方案的钟差序列趋势吻合得相对较好，但是存在明显的系统性偏差，究其原因主要集中在GBM卫星产品中BDS-2和BDS-3系统的处理方式、接收机不同系统间的信号环路硬件延迟等方面。同样地，对于BRCH-TP01的长基线链路而言，BDS-3和BDS-2 Vondark平滑残差的RMS分别为0.202ns 和0.203ns。对于TP02-TP01而言，BDS-3和BDS-2残差的RMS分别为0.022ns和0.033ns。

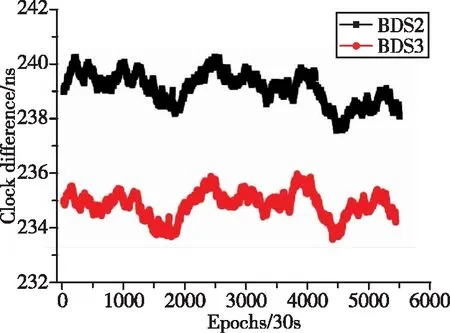
图7 基于载波相位法获取的BRCH-TP01链路钟差序列Fig.7 Clock difference sequence of BRCH-TP01 link based on carrier phase method

图8 基于载波相位法获取的TP02-TP01链路钟差序列Fig.8 Clock difference sequence of TP02-TP01 link based on carrier phase method

图9和图10分别给出了载波相位法获取的BRCH-TP01和TP02-TP01链路的Allan方差。从图中可以看出，在长基线链路中，BDS-2与BDS-3的频率稳定度基本相当，万秒稳定度能达到10-14量级；对于共钟短基线链路而言，BDS-3的频率稳定度要明显优于BDS-2，其万秒稳定度能达到10-15量级。

图10 载波相位法获取的TP02-TP01链路的Allan方差Fig.10 Allan variance of TP02-TP01 link by carrier phase method

3 结论

本文主要研究了基于BDS-3的时间频率传递方法，分析了GNSS共视法和载波相位法的基本数学模型，最后分别对国际时间实验室的长、短基线BDS-2和BDS-3时间传递链路的噪声水平和频率稳定度进行了对比分析，可得出如下结论：

1)在基于共视法的BDS时间传递实验中(2天)，BDS-3方案的钟差序列的噪声水平明显优于BDS-2方案，其平滑残差的RMS在长基线BRCH-TP01链路上分别为1.48ns (BDS-3)和3.13ns (BDS-2)，在短基线TP02-TP01链路上分别为0.65ns (BDS-3)和1.02ns (BDS-2)。但是，两种方案的钟差序列存在明显的系统性偏差，需要在后续的链路标定中予以考虑。此外，BDS-3与BDS-2方案的Allan方差在2条时间传递链路上均符合典型的1/τ的规律，BDS-3明显优于BDS-2，万秒稳定度能达到10-13量级。

2)在基于载波相位法的BDS时间传递实验中(2天)，虽然BDS-3方案的钟差序列与BDS-2也存在明显的系统性偏差，但是其变化趋势显示两者吻合度较好。在噪声水平方面，BDS-3和BDS-2相当，对于长基线BRCH-TP01链路，其平滑残差的RMS分别为0.202ns (BDS-3)和0.203ns (BDS-2)；对于短基线TP02-TP01，其残差的RMS分别为0.022ns (BDS-3)和0.033ns (BDS-2)。在频率稳定度方面，长基线BRCH-TP01链路上，BDS-3和BDS-2相当，其万秒稳定度能达到10-14量级；对于共钟短基线链路而言，BDS-3明显优于BDS-2，其万秒稳定度能达到10-15量级。

3)结合共视法和载波相位法的数学模型和实验结果，考虑到GNSS载波相位法时间传递中使用了观测精度较高的载波相位观测值，时间传递模式不受距离限制，其时间传递的噪声水平及频率稳定度指标明显优于共视法，在长基线的时间传递链路中更为显著。

随着我国BDS-3全球卫星导航系统的不断建设与完善，与其他诸如卫星双向、光纤等技术设备并址的BDS-3观测数据也将得到广泛积累，可以结合这些技术手段进一步评估BDS-3的时间传递性能。