防空导弹任务规划与协同控制技术研究
何飞毅,沈 洁,陈光山,廖幻年
(1.上海航天控制技术研究所,上海,201109;2.上海航天技术研究院,上海,201109)
0 引言
当前协同技术在航天、航空等领域已经得到广泛研究[1-2],随着网络中心战概念的不断深化,未来作战环境将更加复杂,防空导弹面临着作战任务多样、作战空域扩大和作战自主化需求等多方面的挑战。协同任务分配与协同制导技术作为多弹协同的重要组成部分,对于提升防空导弹的集群对抗能力具有重要意义。
在任务分配方面,国内外学者目前主要针对任务分配建模和任务分配算法进行了研究,并将其广泛应用于无人机对敌压制任务中[3]。Ozalp等采用多旅行商模型解决了单一类型任务的多无人机任务分配问题[4]。邢焕革等通过无人机执行任务代价、任务潜力和任务收益三方面建立了任务分配模型,并设计了基于买卖合同策略的粒子群优化算法进行协同任务规划[5]。张耀中等针对多无人机任务存在的特定时序耦合约束问题,采用基于遗传算子的混合引力遗传搜索算法求解协同任务决策模型[6]。肖刚等针对无人机集群多目标任务分配问题,提出了改进量子蚁群算法,提高了集群无人机任务分配效率[7]。
在协同制导方面,国内外学者的研究则主要集中于设计时间/角度协同制导算法。李桂英等针对多枚导弹同时拦截高机动目标的问题,基于终端滑模控制方法和一致性原理设计了多弹协同制导律,在视线方向上实现了时间协同,并保证了视线角收敛到指定终端角[8]。张聪针对反舰弹道导弹一体化协同制导控制的问题,基于一致性理论和扩张状态观测器理论,实现了导弹空间构型稳定和攻击角度一致性[9]。
综上所述,协同任务分配与协同制导技术已经取得了丰富的研究成果,但是应用对象主要是亚音速导弹或低速飞行的无人机。对于飞行速度为2~3Ma的防空导弹协同作战,任务分配需要在满足最优拦截的基础上,更加注重保证导弹的命中精度。在任务分配完成后,由于弹目相对速度和角度较大,导弹末制导无推力飞行,滑模制导和扩张状态观测器等非线性制导方法容易在飞行初始阶段产生大过载需求,最终导致难以兼顾时间/角度约束和命中精度的需求。
本文首先对防空导弹协同作战的特点进行了分析,提出了防空导弹面对群目标时的协同作战框架。然后通过能力预测建模描述多弹拦截目标的能力,并采用改进的粒子群优化算法进行任务分配。在任务分配的基础上,采用弹道成型和偏置比例导引思想,结合一致性理论,设计了时间/角度协同制导律,保证防空导弹能够在满足命中精度需求的基础上实现分布式协同作战。最后通过典型作战场景下的六自由度仿真,验证了方案的有效性。
1 防空导弹协同作战特点
传统上防空导弹拦截目标主要采用单对单的方式,在面对巡航导弹和战机等来袭群目标时,一方面随着目标机动能力和干扰能力的提高,导弹容易在拦截过程中丢失目标;另一方面,由于高威胁和高价值目标隐藏在集群中,使得导弹发射后很难改变拦截目标。采用协同作战将有助于提高对群目标的拦截效率:1)导弹发射后可根据实时探测信息快速改变拦截目标的能力;2)可对不同威胁、不同价值的目标进行差异化拦截;3)可在复杂干扰下高效拦截机动目标,降低目标不可逃逸区。因此,快速任务分配和分配后的协同制导是防空导弹协同作战发展的必然趋势。
一般任务分配包括完全集中式、完全分布式、分层集中式和分层分布式四种框架。考虑到防空导弹协同作战效率、实时性和抗干扰需求,本文建立了如下集中-分布式任务分配框架,有效提高了任务分配效率。

图1 集中-分布式任务分配框架Fig.1 Centralized-distributed task assignment framework
在上述框架下,各导弹依靠指挥中心承担大量级的任务分配;各弹根据分配目标形成协同制导编队,编队内部具备分布式规划能力,可以承担小范围的分配任务,并且编队中各弹通过协同制导对复杂干扰下的机动目标进行探测和拦截。
2 多弹协同任务分配方案
基于任务分配框架,本文首先从拦截距离、机动代价、转弯角度三方面,预测导弹在任意空域中拦截目标的能力,然后通过改进粒子群优化算法进行快速任务分配。
2.1 导弹能力预测模型
假设导弹i与目标j的距离矢量为rij,rmax为导弹最大拦截距离,则归一化后的距离代价为
Jdistance=|rij|/rmax
(1)
机动代价用零控脱靶量dij表示,则归一化后的机动代价为
Jmaneuver=dij/max{dij}
(2)
转弯代价用ψij表示,则归一化后的转弯代价为
Jangle=ψij/ψmax
(3)
综合上述代价可得到导弹i攻击目标j的代价为
cij=λ1Jdistance+λ2Jmaneuver+λ3Jangle
(4)
式中,λ1、λ2、λ3为权重系数,且λ1+λ2+λ3=1。
则m个导弹攻击n个目标的代价函数为
(5)

考虑不同的任务类型和实际约束条件:
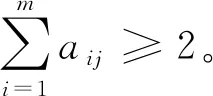
2.2 改进粒子群优化算法
上述任务分配模型为带约束的多目标优化问题,本文结合文献[10-11],采用改进的粒子群优化算法进行求解。
考虑到任务分配的离散特点,采用离散化的粒子表示方式,如表1所示。

表1 单个粒子形式
表1中,第一行为导弹序号,根据实际导弹数目进行排序,且序号固定;第二行为目标序号,通过随机数进行初始化,且被限定在[1,n]内变化。若粒子群数量被定义为N,则整个优化空间的维数为N×m维。
同时对于如下粒子更新公式

(6)
式中,r1、r2、RandT为[0,1]上的随机数;ω为惯性权重;c1、c2为学习因子。
为了保证优化过程具有较快的搜索速度,并加强在搜索初期的全局搜索能力和搜索后期的局部搜索能力。采用自适应线性权重系数
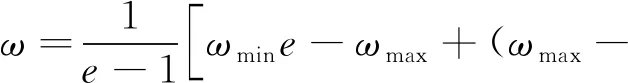
(7)
式中,ωmax为惯性权重最大值;ωmin为惯性权重最小值;e根据经验确定;k为迭代次数;Smax为最大迭代次数。
采用动态学习因子进一步提高算法的搜索能力,学习因子变化规律为
c1=c10-(c10-c1f)(k/Smax)
c2=c20+(c2f-c20)(k/Smax)
(8)
式中,c10、c1f分别为学习因子c1的初值和终值;c20、c2f分别为学习因子c2的初值和终值。按照较大的c1提高局部搜索能力,较大的c2提高全局搜索能力的原则取值。
3 多弹时间/角度协同制导方案
根据任务分配结果,多弹集群将被划分为多个编队的形式进行作战。对于具有较强干扰能力和机动能力的目标,需要多枚导弹同时对目标进行拦截或多角度探测抗干扰。本文分别采用弹道成型和偏置比例导引思想,结合一致性理论,设计了多弹时间/角度协同制导律,同时满足多弹协同制导和命中精度的需求。
3.1 时间协同制导律
一般导弹速度远大于目标速度,即Vm≫Vt,导弹拦截目标的剩余飞行时间tgo主要由Vm决定,因此考虑导弹运动模型如下
(9)
式中,θ为弹道倾角;a为纵向加速度;aB用于减小脱靶量;实现命中目标;aF用于调整飞行时间,实现时间协同。
将上述相对运动模型转化为具有终端时间限制条件的最优控制问题[12]
(10)
式中,所有变量均进行了归一化处理,有
(11)
根据弹道成型制导思想,定义如下目标函数
(12)
导引时间约束为
(13)
基于极大值原理求解上述带约束的最优控制问题,可以得到满足导引时间约束的最优制导律为
(14)
Kt=(-120V5)/(aBr3)
(15)
3.2 角度约束制导律
本文基于偏置比例导引[13]设计角度协同制导律,考虑如下相对运动模型。
(16)
式中,q为弹目视线角;r为弹目相对距离。
偏置比例导引律的一般形式为
(17)
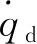
将式(17)代入式(16)并忽略导弹轴向加速度和目标加速度项可得
(18)
假设tf时刻以角度qf命中目标,求解式(18)可得
(19)
进而得到满足终端角度qf的加速度指令为
(20)
3.3 基于弹间通信的协同制导方案
一般多弹通信关系可通过强连通有向图表示[14]。假设编队中存在m个导弹的信息交互,将其通过Laplacian描述如下
(21)
式中,lij表示导弹i与导弹j的连接关系,且有
(22)
对于带通信的多弹分布式协同制导问题,假设要求各弹某一指标ξ=[ξ1,ξ2,…,ξm]T趋于一致,则可通过如下分布式加权平均一致性协调算法[15]实现

(23)
式中,C=diag(c1,c2,…,cn)。
本文考虑到导弹拦截精度问题,纵向运动采用传统比例导引保证命中目标,侧向机动通过协同制导律满足时间/角度约束需求,
纵向运动制导采用传统的比例导引方法,即
(24)
将式(21)代入式(14)中,可得多弹时间协同侧向制导律为
(25)
将式(21)代入式(20)中,可得多弹角度协同侧向制导律为
(26)

4 仿真验证
4.1 仿真场景设置
本文通过4枚导弹拦截3个目标的六自由度仿真,验证了方案的有效性。导弹发射后某一时刻的初始运动状态如表2所示。

表2 导弹初始运动状态
目标做匀速运动,其运动状态如表3所示。

表3 目标初始运动状态
设立如下仿真场景:1)目标1、2为当前已知目标,目标3在某一时刻被发现;2)目标1需要20°探测角探测,目标2需要同时拦截;3)导弹最大拦截距离为35km,最大机动角度为20°。
4.2 仿真结果分析
在46.5s开始仿真,64.5s发现目标3,76s结束。任务分配算法参数如表4所示。

表4 任务分配算法参数
协同制导算法参数如表5所示。

表5 协同制导算法参数
对上述场景进行六自由度仿真,得到的仿真结果如表6和图2~图7所示。
表6、图2、图3为任务分配仿真结果,仿真初始时刻4枚导弹通过任务分配形成了2枚导弹为编队拦截1个目标的态势,在64.5s发现目标3后,导弹重新分配目标。从图4和图7可以看出,导弹2改变了既定目标,且各弹脱靶量均小于5m。从图6可以看出,导弹2和导弹4的探测角不断增大,且在64.5s前形成了约19.51°的探测角,与期望值相差约0.49°。从图6可以看出,导弹1和导弹3在72s命中目标前剩余飞行时间误差不断减小,命中时间差小于0.5°。
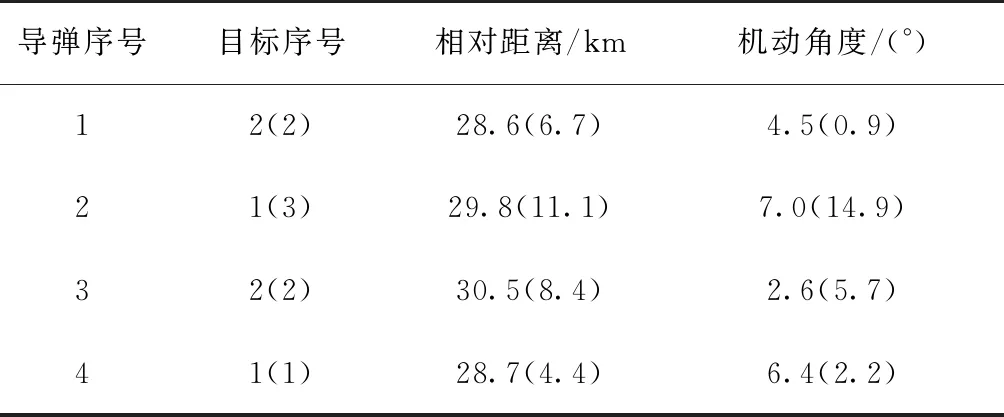
表6 任务分配结果

图2 初始时刻分配迭代次数Fig.2 Distribution iterations of initial time

图3 新增目标后分配迭代次数Fig.3 Distribution iterations after updating target

图4 弹目相对距离Fig.4 Missile-target relative distance
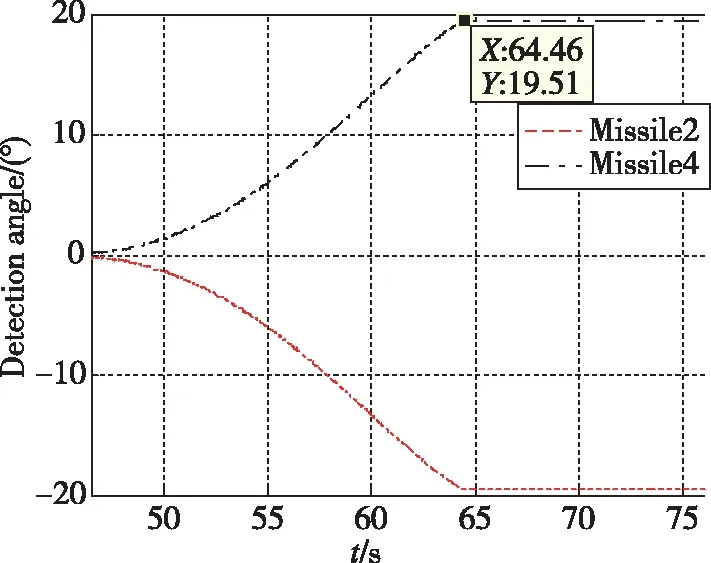
图5 导弹探测角Fig.5 Missile detection angle

图6 导弹剩余飞行偏差Fig.6 Missile time-to-go deviation
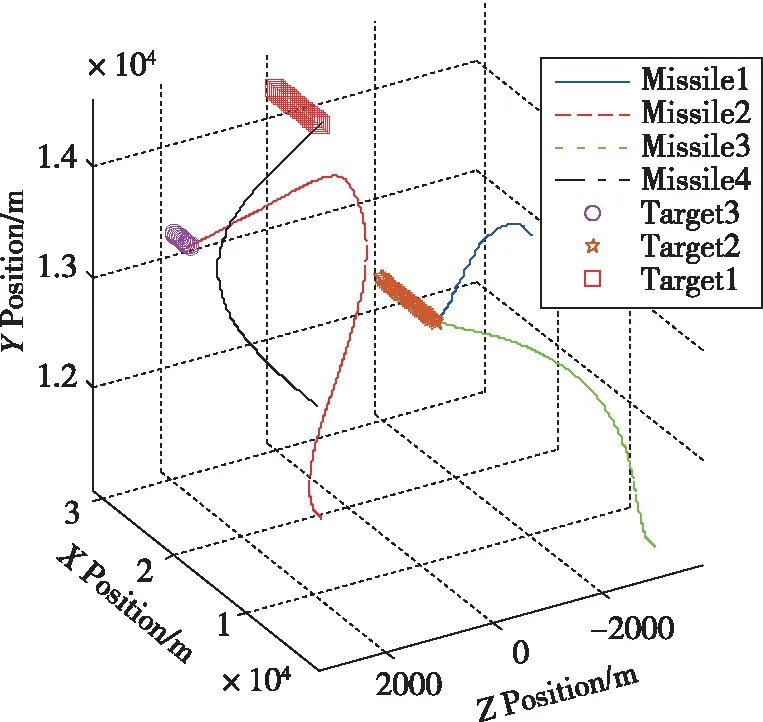
图7 三维轨迹Fig.7 Three dimensional trajectory
基于上述场景,采用文献[16-17]的滑模制导方法进行时间/角度协同制导对比仿真,导弹过载限幅20g,导弹3和导弹4的侧向过载变化对比曲线如图8所示。
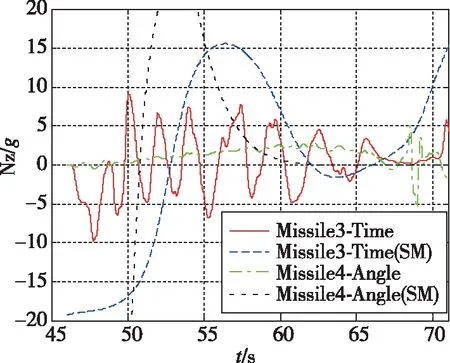
图8 侧向过载变化对比Fig.8 Comparison of lateral overload
从图8可以看出,与滑模制导等非线性制导方法相比,采用本文的时间/角度协同制导方法在初始时刻过载需求更小,且末端弹目距离变小时,因命中需求导致过载快速增大的持续时间更短,有利于降低脱靶量,可见本文方法更适用于工程应用。
5 结论
本文针对防空导弹面对群目标时的协同拦截问题,提出了一种多弹协同任务规划与制导方案。主要结论为:
1)本文采用的基于导弹拦截目标能力预测的快速任务分配方法,在传统以飞行路径进行规划的基础上,通过增加机动和转弯代价兼顾导弹的命中精度要求,为后续解决大弹目相对速度条件下的快速任务分配提供了思路。
2)通过设计基于多弹交互信息的时间/角度协同制导律,能够实现不依赖于对期望命中时间/角度的初始规划,使多弹作战具有更高的自主性和灵活性。同时与滑模制导等非线性制导方法相比,在多弹时间/角度约束下的初始过载需求更小,末端更容易命中目标。
3)本文所提的防空导弹协同任务规划与制导方法主要采用简化的模型进行设计,后续需要通过更加精确的建模和分析进行完善,以提高方法的工程应用能力。

