高精度二维指向光电跟踪平台设计

杨鹏 李晓 赵鑫 于飞 连华东

（北京空间机电研究所，北京 100094）

0 引言

天基空间光学监视系统是天地一体化感知网络的重要组成部分，是空间目标监视跟踪的重要手段，具有不受大气影响、测量精度高、可近距离精确成像的优势[1]。从2006年开始，美国航天局、加拿大、欧洲航天局、日本等国家和组织相继开始实现了在轨成像跟踪卫星的研制、发射验证和应用[2-4]。

天基空间光学监视系统以美国“地球同步空间态势感知计划”（GSSAP）系列卫星和美国天基空间监视系列卫星（SBSS）为代表。二者采用不同的技术手段，GSSAP卫星部署在GEO轨道（地球静止轨道）之上和之下的漂移轨道中，通过大量的在轨机动接近观测目标，最近的观测距离可达10km的位置，再利用星上光学载荷进行监视观测。SBSS卫星目前在轨1颗，运行于高度为630km的太阳同步轨道，完成全地球同步轨道带目标的观测。其配置1台300mm口径双轴凝视成像相机，安装在双轴万向节上，平均每天进行15 000次观察，可以监测地球同步轨道上的小于1m3的物体，可以提供目标物体轨道数据，预测其运行轨迹，避免碰撞的发生[5]。

从19世纪70年代起，国外已经开始发展并逐步完善了二维指向机构技术，80年代起开始在不同类型、不同轨道的卫星中实现了成功应用。目前该技术已先后在军事通信卫星、数据中继卫星、对地观测卫星、星际探测卫星和军用侦察、导航等卫星上得到广泛的应用[6-10]，精度指标已达到较高水平[11]。

本文设计一种高精度二维指向光电跟踪平台，搭载大口径光学相机，实现空间目标的高精度跟踪监视。同时考虑运动载荷较大对整星姿态产生的影响，以及整星姿态控制精度对高目标跟踪精度的影响[12]，在光电跟踪平台上设计安装惯量补偿装置，通过系统仿真分析验证，可以满足系统高跟踪精度、高跟踪稳定度的应用要求。

1 总体设计

1.1 系统设计

根据任务和卫星总体分解的光电跟踪平台系统指标如表1所示。

表1 光电跟踪平台系统指标Tab.1 System requirements of the electro-optical tracking platform

光电跟踪平台主体结构和坐标系定义，如图1所示，从相机通光口径看去，垂直向下为Z轴，水平向左为Y轴，X轴与Y、Z轴均正交，符合右手定则。光电跟踪平台主要包括二维指向机构、跟踪相机和光学载荷。其中二维指向机构承载光学载荷和跟踪相机二维高精度转动，实现空间目标跟踪和监视。跟踪相机配合控制系统，实现光电跟踪平台高精度指向控制。光学载荷质量约为100kg，口径为560mm，负责拍摄空间目标的光学影像，载荷指标达到国内外先进水平，也是目前空间高精度二维指向机构承载的最大有效载荷之一。

1.2 系统关键指标分析

（1）目标跟踪性能分析

目标跟踪精度（指向偏差）：0.01°(3σ)

目标跟踪稳定度（速度偏差）：≤0.042(°)/s(3σ)，（角速度在1～2.5(°)/s区间）；≤0.0042(°)/s(3σ)，（角速度≤1(°)/s）

平台的精度指标非常之高，负载又大，需要选用极高精度的测角元件，以及高精度、大输出力矩的电机。

图1 光电跟踪平台主体结构Fig.1 The main structure of the electro-optical tracking platform

（2）角动量干扰分析

光电跟踪平台系统转动负载惯量较大，工作过程中因为运动姿态的改变，会对整星的姿态控制产生干扰。

角动量计算公式为L=J×ω（其中L为角动量；J为轴上的转动惯量，俯仰轴为7.4 kg·m2，方位轴17kg·m2；ω为角加速度，两轴的最大转动角速度均为6(°)/s）。

根据公式可以计算，俯仰轴最大角动量为0.77 N·m·s，方位轴最大角动量为1.78N·m·s。两个轴都不能满足整星平台姿轨控对残余角动量小于0.5 N·m·s的要求。因此在跟踪平台上需要在俯仰轴和方位轴都加入动量补偿设备，抵消转台的跟瞄运动对整星平台的影响。

（3）稳定性能分析

整星能够实现姿态及控制精度有限，姿态指向精度（成像期间）优于±0.018°，姿态稳定度（成像期间）优于 0.005(°)/s。然而，光电跟踪平台的跟踪精度要求优于±0.014°，且当目标运动角速度不高于1(°)/s时，单轴跟踪稳定度要优于 0.004 2(°)/s。可见，整星控制性能难以满足高精度、高稳定度跟踪的需要，因此在光电跟踪平台上要加入惯性稳定环节，来补偿整星平台的不稳定的姿态控制。

2 结构设计

结合任务需求和指标分析，设计光电平台二维指向机构，如图2所示。整体上采用模块化设计，主要包括方位轴驱动组件、方位轴动量轮、俯仰轴驱动组件、U型支架、俯仰轴轴承座组件（包括制动器）、俯仰轴动量轮（对置安装）等。

驱动元件选用永磁同步电机，具有结构简单、功率密度大、效率高、运行可靠、环境适应能力强的特点。选用国产 24位绝对式光电编码器，角度误差不大于±2.8″，起到反馈两轴角度位置作用，用于控制系统闭环。光电转台驱动组件采用模块化一体设计的思路，电机和编码器本身不自带轴承，共用驱动组件轴承以节省重量。驱动组件设计时，将永磁同步电机、光电编码器、轴承、输出轴按模块集成为一个整体，可作为独立成套部件直接应用到转台机构中。

俯仰轴驱动组件如图3所示。俯仰轴轴系包括安装底座、转轴、转接法兰、电机法兰、轴承挡圈等结构件。采用一对背对背安装角接触球轴承，配合一个深沟球轴承，采用一端固支，一端游动的支撑方式，满足轴系支撑刚度，减小轴系热变形影响。

图2 光电平台二维指向机构Fig.2 The two-dimension pointing mechanism of the electro-optical tracking platform

图3 俯仰轴驱动组件Fig.3 The drive assembly around the pitch axis

3 控制设计

光电跟踪平台根据任务要求能实现多项任务模式，控制系统十分复杂。本文着重介绍控制器组成、角动量补偿回路、速率陀螺稳定回路等。

3.1 控制器组成方案

为实现光电跟踪平台高精度控制，设计采用一个FPGA（Field-Programmable Gate Array，现场可编程门阵列）和两个DSP（Digital Signal Processing，数字信号处理器）的多处理器的高精度控制伺服电路，由控制器电路和功率驱动电路两部分构成，其中，控制器电路包括电源综合管理单元、DSP控制核心电路，FPGA控制核心电路、ADC（Analogue-to-digital Conversion，模数转换器）转换电路、通信电路；功率驱动电路包括母线电源及其保护电路、功率驱动电源电路、位置检测电路、电流检测电路、PWM（Pulse Width Modulatio，脉冲宽度调制）信号光耦隔离及端口电路、功率驱动电路。系统组成框图如图4所示。

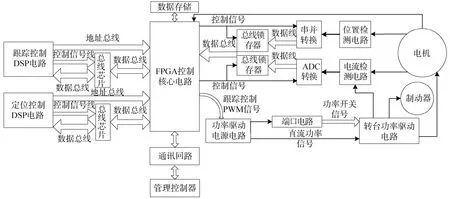
图4 光电平台控制系统框图Fig.4 The control system frame diagram of the electro-optical tracking platform

3.2 角动量补偿回路

经分析可知，由于转台转动惯量较大，单个较大转动惯量载荷体运动时，与卫星发生耦合作用使卫星系统参数不断变化，系统模型出现不确定性，降低卫星姿态稳定度，成像出现误差，图像发生扭转与平移，成像品质下降[13-18]，因此在目标跟踪过程中需要动量补偿回路。

动量补偿回路根据光电码盘计算出转动的绝对角速度，然后对动量轮进行控制。通过动量轮的转动来补偿转台在跟瞄过程中的角动量，保证转台补偿后的残余角动量在合理的范围内。补偿回路的实现原理如下图5所示。

图5 动量补偿回路的实现原理Fig.5 The momentum compensation principle circuit

利用动量轮进行转速与转台转动惯量对应比例的反向转动，可以补偿转台转动中转动速度、转动加速度对卫星平台的影响。有ωc/ωd=Jd/Jc，其中ωc和ωd为转台和动量轮的角速度，Jc和Jd为转台和动量轮的转动惯量。

为消除俯仰轴动量轮对方位轴的进动力矩影响，俯仰轴采用2个相同动量轮对置安装方式。根据对俯仰轴和方位轴在力矩和角动量的分析计算，选取动量轮的指标如表2所示：

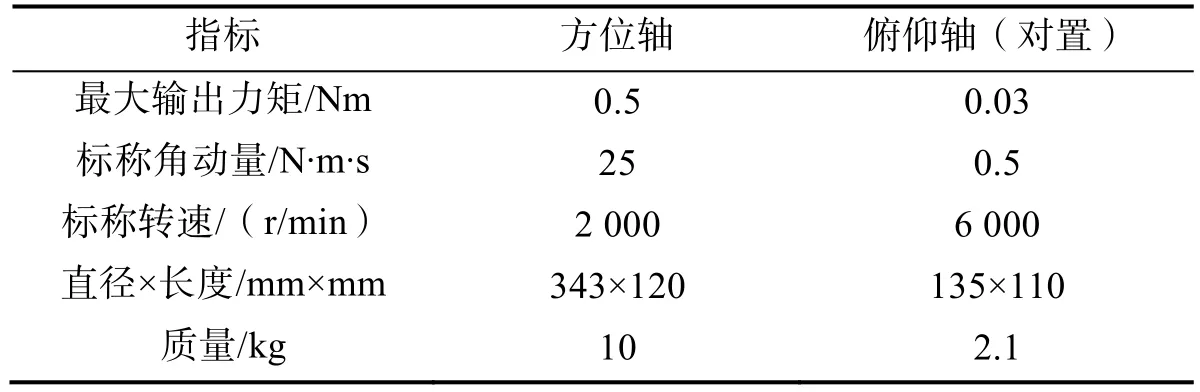
表2 方位轴及俯仰轴动量轮指标Tab.2 Requirements of the momentum wheel for the azimuth and pitch axes

3.3 速率陀螺稳定回路

方位和俯仰两个方向分别利用相应空间方向的速率陀螺作为反馈，来抑制卫星平台对指向跟踪转台的干扰。稳定回路框图，如图6所示。图中，iθ为目标角位置；为平台颤振引起的角速率变化；为视轴相对平台的角速率。

图6 稳定回路框图Fig.6 A diagram of the stabilization loop

根据总体指标，即系统带宽≥40Hz，隔离度≤0.5%，超调量≤20%，选择速率陀螺的指标如表3所示。

经计算，俯仰角速度陀螺稳定回路开环传递函数G(s)为：

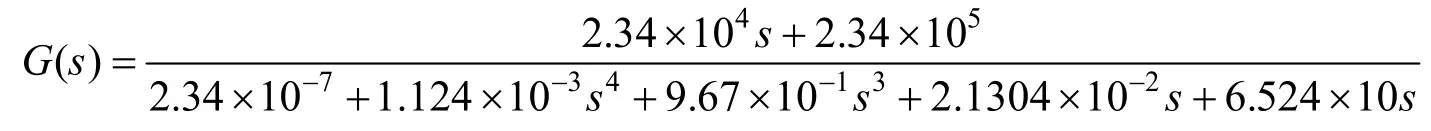
俯仰角速度陀螺稳定回路闭环传递函数Φ(s)为：

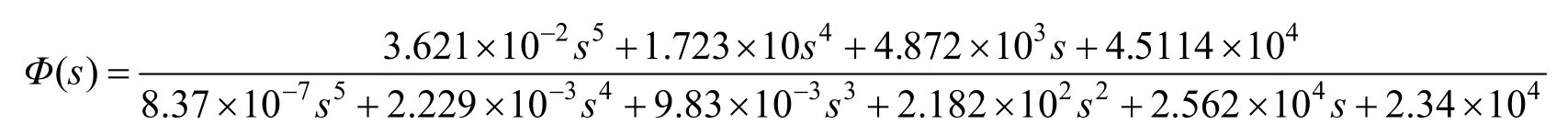
俯仰角速度陀螺稳定回路闭环幅频特性如图7所示，回路带宽为268rad/s，即42.7Hz，满足系统指标要求。

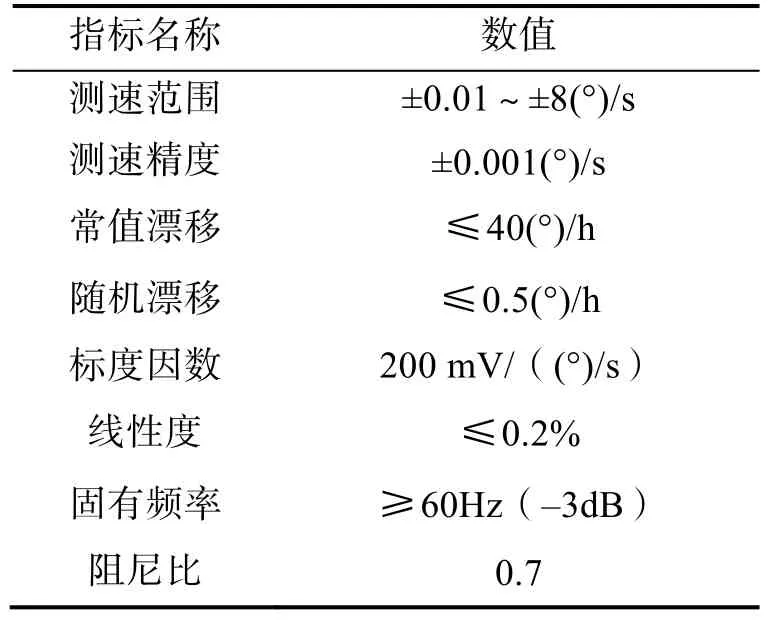
表3 速率陀螺指标Tab.3 Design requirements of the rate gyro

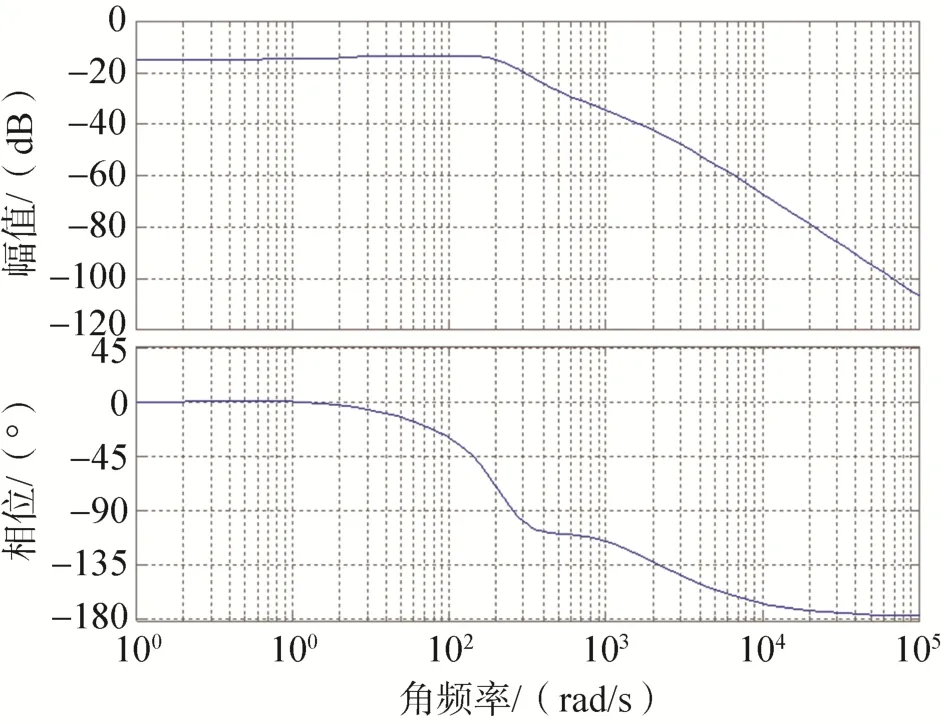
图7 俯仰角速度陀螺稳定回路闭环幅频特性Fig.7 Close loop amplitude frequency characteristics

产品逐次通电（间隔不小于24h）三次，零位电压变化量应不大于3mV，标度因数变化量应不大于1mV/（(°)/s）。

方位角轴计算过程从略，方位角速度陀螺稳定回路带宽为270rad/s，即42.9Hz，满足系统指标要求。

3.4 系统控制方案

光电跟踪平台系统控制方案在目标搜索阶段以高精度光电码盘作为位置回路的角度反馈，内环是由速率陀螺组成的稳定回路，此时的角度按照搜索条件选择的角度曲线，如使角度按照斜坡函数输出就可获得匀速速度输出。当通过成像系统捕获目标后，切换到目标跟踪回路工作，此时图像处理系统产生脱靶量信息作为位置回路的角度反馈，角度指令的输入为零。

在原始系统分析中，位置调节器、转速调节器、电流调节器均暂时用微分环节表示，在后续模型中需要考虑其中的转速滤波、电流滤波、角位移滤波，在原始系统分析中，暂时用一阶惯性环节表示[19-21]。

以俯仰轴为例，对跟踪控制器进行仿真建模，绘制出闭环系统的频率响应，以波特图的形式，如图8所示。其中-3dB对应的频率是系统的截止频率，也就是校正后系统的带宽。截止频率为：46.2rad/s，即带宽为7.35Hz，满足带宽优于4.8Hz的要求。

为验证轴系转动刚度是否满足控制带宽要求，对光电平台二维指向机构进行模态分析。其中光电载荷及2组动量轮采用质量点代替，工况为解除火工锁状态。其中前两阶模态与轴系扭转无关，第三阶模态为方位轴扭转，如图9所示。此时频率为68.9Hz，约为控制带宽7.35Hz的10倍，满足系统带宽要求。

4 系统仿真

本文对成像跟踪过程中的运动精度和速度稳定性进行仿真。考虑到跟踪的精度、稳定度对闭环带宽的需求与成像帧频、成像处理时延的矛盾，在成像跟踪控制中利用卡尔曼滤波的运动滤波、运动预测功能，进行目标的运动估计运算。从而提高测量带宽和测量精度，确保跟踪控制的性能要求。

考虑在不同距离监视跟踪同一轨道的目标，光电跟踪平台方位轴运动轨迹会有所不同，如图10所示。选择极限运动曲线进行分析，即最大跟踪角速度为2.5(°)/s，最大角加速度为1(°)/s2的运动轨迹。

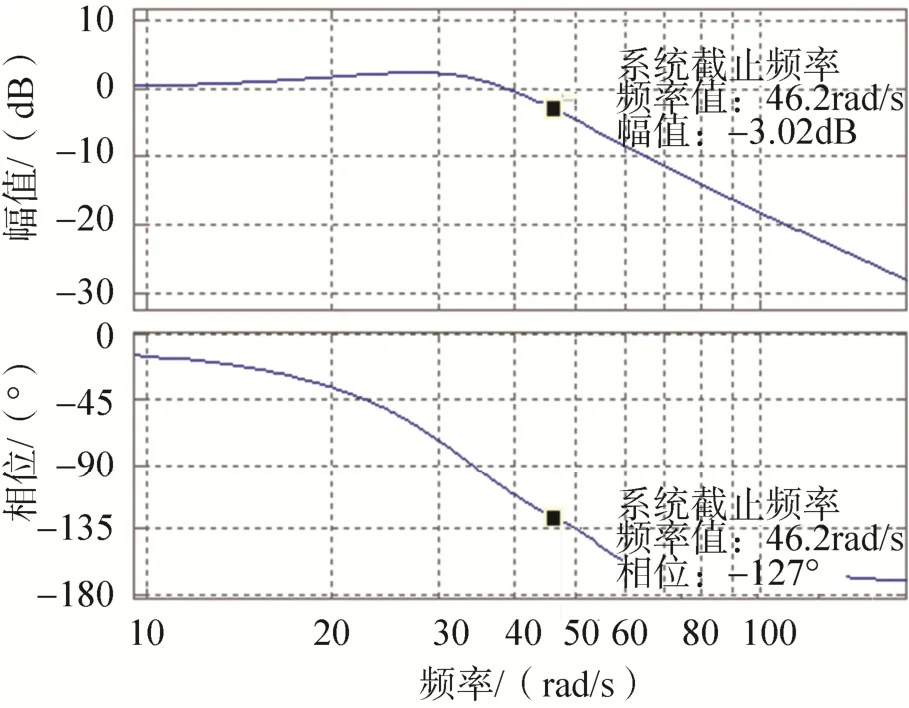
图8 俯仰轴跟踪回路闭环波特图Fig.8 The bode plot of closed loop tracking of the pitch axis

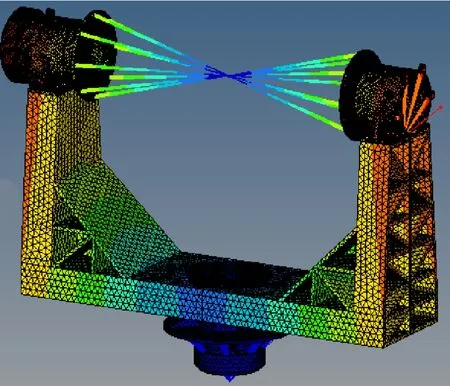
图9 第三阶模态仿真结果Fig.9 The 3rd modal simulation results

目标极限运动的成像跟踪的指向偏差结果如图11所示，在450～550s区间段，运动变化较为剧烈，在此段会有指向偏差峰值，在500s时刻方位轴运动由加速运动变为减速减速运动，此时指向误差过 0点，符合物理实际。根据仿真结果，指向偏差峰值为0.006 4°，满足单轴成像跟踪精度0.01°(3σ)的指标要求。

目标极限运动的成像跟踪的速度偏差仿真结果如图12所示，由图10运动曲线可知在480s和520s时刻，加速度达到最大值且变化最为剧烈，此时速度偏差出现峰值，可以获得角速度在1～2.5(°)/s区间段跟踪稳定度优于0.004 5(°)/s，能够满足单轴跟踪稳定度优于 0.042(°)/s(3σ)的指标要求；在角速度≤1(°)/s区间段跟踪稳定度优于0.002 4(°)/s，能够满足单轴跟踪稳定度优于0.004 2(°)/s(3σ)的指标要求。

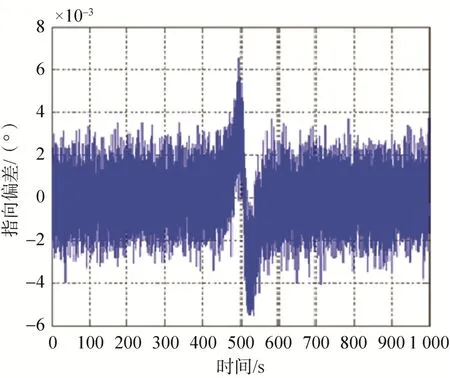
图11 成像跟踪指向偏差仿真结果Fig.11 Simulation results of the imaging tracking pointing deviation

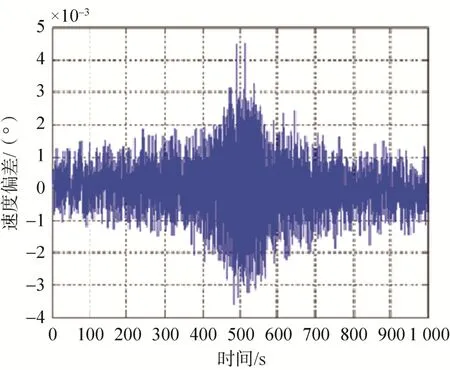
图12 成像跟踪的速度偏差仿真结果Fig.12 Simulation results of the imaging tracking speed deviation

5 结束语

本文针对某型空间大口径高精度光电跟踪平台的特殊应用环境，提出采用动量补偿系统解决平台运转对整星的影响的问题，提出采用在载荷上安装高精度速率陀螺解决整星控制精度不足的问题。在此基础上，搭建控制系统方案，对目标极限运动轨迹跟踪下,系统跟踪性能进行仿真验证，结果表明：

在最大跟踪角速度为2.5(°)/s，最大角加速度为1(°)/s2的目标极限运动轨迹跟踪情况，光电跟踪平台跟踪精度和稳定度均可满足指标要求，仿真结果为后续产品研制打下良好基础。