初中数学复习课的教学实践与思考

摘 要：数学复习课要具备明确价值、突出主题、实现回眸、显现架构、经历生长、调动思维五个要素。在“圆的再认识”这节复习课的教学实践中，设计了画图、识图、释图、构图、论图五个教学环节，着力促进了学生的三个生长点。

关键词：复习课;实践;思考

春秋时期，孔子在教学上有着丰富的经验，他常常与学生一起研讨问题，并给学生解决各种疑难问题，他在《论语》中提出：“学而时习之，不亦说乎？”“温故而知新，可以为师矣。”这些都在告诫我们：学习的东西要时常去复习、去实践，只有这样，才能不断地加深记忆，最终将知识化为己用。

数学复习课是根据学生的认知特点和规律，在学习的某一阶段，以巩固、梳理已学知识、技能，促进知识系统化，提高学生运用所学知识解决问题的能力为主要任务的一种课型。其目的是温故知新，查漏补缺，完善认知结构，促进学生解题思想方法的形成，发展数学能力，促进学生运用数学知识解决问题的能力。

文章基于上述思想，结合圆的再认识这一教学活动，谈谈自己关于复习课的实践与思考。

一、 复习课要明确价值

在数学复习中，我们必须要明确，存在的最大问题是什么？阻碍学生提高数学成绩的最大障碍是什么？唯有如此，才能真正提高效率，让学生感受到数学复习的价值。

圆是初中阶段曲线形的代表，它具有与直线型完全不同的性质，无论是从知识的学习、技能的训练或数学思想方法的渗透，都为我们提供了一些新的视角。

从完善对几何知识的认识的角度看：圆提供了一种新的认识图形的方式（研究方法、思维方法的不同，并解决了证明中需要穷举的证明方法（反证法））。通过复习，学生会对圆有一个较为全面系统的认识，而且对各种数学思想如分类讨论，转化思想，完全归纳、类比的思想等有很好的理解和把握。

二、 复习课要突出主题

复习绝不是对旧知识的简单重复，而是学生认识的继续、深化和提高。平时教学中点状、零散的知识需要系统化，成为线状、网状。平时学生所学知识的疑惑点需要澄清，平时所学知识中重要的思想方法需要提炼，以凸显“让学生又一次发展”的教学理念。如果说新授课是“画龙”，复习课则是“点睛”，那么复习课的主题就是“睛”。

圆的复习突出用圆的对称性聚合圆的相关知识，对圆进行系统的知识梳理，形成知识体系。在对以圆为背景的直线形问题的生成、分析过程中，培养运用圆的对称性解决问题的意识。

三、 复习课要实现回眸

学生要根据教师搭建的立体式、生长型构架中的“梯子”，重新认识所要复习的知识，并通过知识的生长过程，让学生拾级而上，看清数学本质，达到一定的认知高度，形成“一览众山小”的体验，切实提高问题解决的能力，进而提升数学素养。

本节课首先通过圆与其他简单图形的关系对圆进行再认识，进一步树立圆的知识体系，形成知识的结构化和体系化。通过对以圆为背景的直线形问题的生成、分析与理解，进一步深刻理解圆的对称性，一方面能运用圆的对称性，提升对圆的再认识，另一方面能够运用对称变化的观点分析和构造图形。

四、 复习课要显现架构

根据所要复习的知识内容和学生已有的认知经验，坚持系统论理论，运用结构化的思维方法，架设生长型路径，开展探究性活动。生长型架构下的数学复习课是一种行之有效的方法，一改惯用的“框图+例题+练习”的单一做法，而是践行“生长数学”的教学主张。

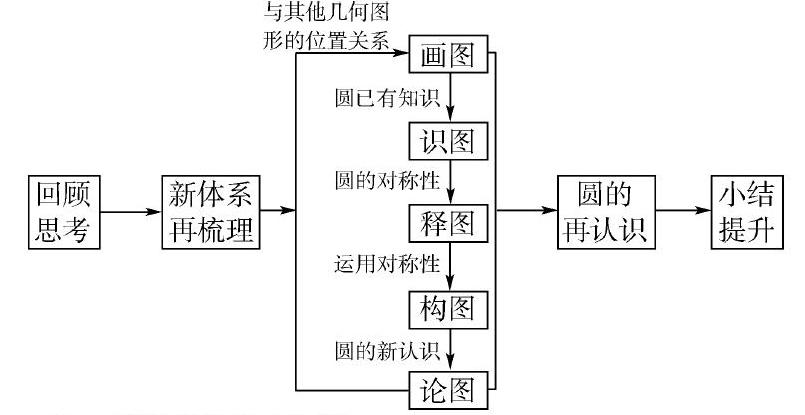
关于圆的复习课，我的生长型架构是：

五、 复习课要经历生长

“新授课育树，复习课育林”，数学教学的价值在于思维教学，思维教学的关键在于创设思维必然的场景，让学生学到具有生长力的数学。让学生从问题中生长思维、从探究中生长学力、从感悟中生长品格、从内化中生长素养。

为达到上述目的，笔者设计了画图、识图、释图、构图、论图五个环节，从而达到了复习的知识在层层推进，学生对圆的认识也在步步生长。

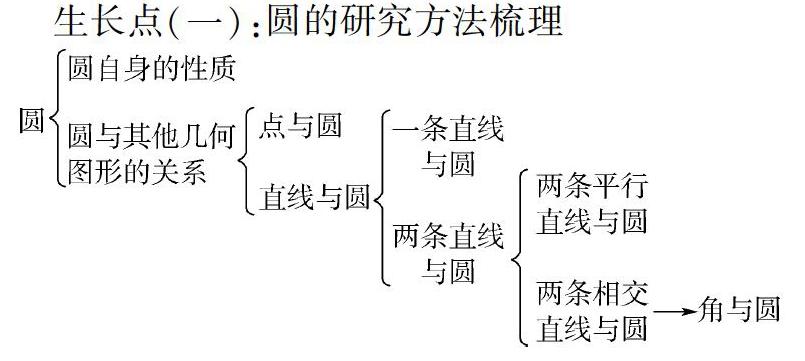
生长点（一）：圆的研究方法梳理

在此处角与圆的关系是一个很好的生长点，为此设计了如下教学活动。

1. 画图识图

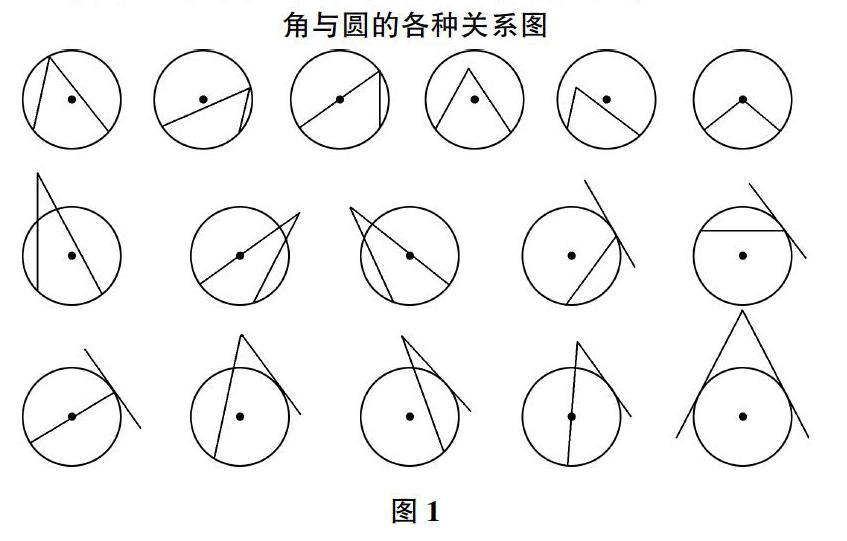
（1）画出圆与角的关系，如图1：

使学生明确再认识圆的思路和方法。

（2）在图1中识别已学过的圆的内容，并解释。

涉及的相关内容有，圆心角、圆周角、圆周角定理、垂径定理、切线的判定，完成对圆的有关知识重新进行梳理。

生长点（二）：针对角与圆的位置关系，选取其中相关联的三种关系图进行再生长。

为此设计了如下教学活动。

2. 释图构图

提出问题：图2中的四边形可不可以是菱形，若不是，需要添加什么条件？

生长点（三）：针对上述圆与角的相关联图形变化，添加或改变图中相关量的条件，看看有什么新的发现？经历第三次生长，为此设计了如下教学活动。

3. 构图论图

添加几何条件，生成新的问题：

在生长图3中：若添加∠C为直角，AB为角平分线;

若添加点A、点O、点B共线。

在生长图4中：若P为半圆的中点，P也为AC的中点;

在生长图5中：若P不为半圆的中点，过点P作圆O的切线PE;

①OE与AC平行，

②点E是BC的中点，

③PE=CE，

④四边形POBE可不可以是平行四边形？若不是，需要添加什么条件？

⑤四边形POBE可不可以是正方形？若不是，需要添加什么条件？

⑥四边形AOEP可不可以是平行四边形？若不是，需要添加什么条件？

学生经历观察、分析、推理、论述、表达等过程，从而让学生经历以圆为背景的直线形问题的生长过程，形成对圆的再认识。

六、 復习课要调动思维

美国教育学家克罗韦尔指出：“教育面临的最大挑战，不是技术，不是资源，不是责任感，而是……去发现新的思维方法。”

为了唤醒学生已有的知识，进行深入的数学思维活动。同时促使学生对所学的知识进行比较、分析、提炼，形成自己的观点。提出了如下两个问题：

问题一：你认为圆中什么内容最重要？为什么？

其核心目的是为了促使学生主动建构知识之间的联系，调动学生的思维。

为了将课上研究的问题进一步的延伸，引发学生进一步的思考。

问题二：从本节课所画图形中选择一个图形，结合圆的对称性，添加几何条件，构成一个新的图形，观察、思考、提出新的有价值的问题。

在复习课的教学中要让学生懂得任何方法都是有思维过程的，你所使用的任何方法不能简单地套用，而是要能够解释你选择这个方法的逻辑。所以教师要坚持思维在前方法在后，克服那种见到某种题型就对应一种方法的教学形态。

参考文献：

[1]张鹤.数学复习课如何提高思维品质[J].中国教师报，2016，6（6）.

[2]卜以楼.生长构架：复习课的理念创新[J].考试研究，2016，10（4）.

[3]卜以楼.让复习课留下一串串生长节[J].中学数学月刊，2013，11（11）.

[4]张鹤.如何做一名优秀的中学数学教师[J].中小学教材教学，2016，3（3）.

作者简介：

邵海磊，北京市，首都师范大学附属中学。