基于演化博弈的高校垃圾分类监管机制研究

郝梦阁， 张冬咏， 郭柯楠

（河南农业大学信息与管理科学学院，郑州 450046）

垃圾分类是垃圾减量化及资源化的主要途径［1］. 截至2017年，全国城市生活垃圾清运量已达2.152 09亿t，并以4%的年增长率递增［2］，解决“垃圾围城”问题，实现垃圾减量化、资源化迫在眉睫. 早在2000年，北京、上海等8个试点城市实施“城市垃圾分类”，但效果并不理想［3］. 目前，大学生占城市居民人口比例逐渐提高，高校校园垃圾已经成为城市生活垃圾的重要组成部分［4-5］.

一直以来，垃圾分类都颇受学者们的关注，从经济和管理的角度来看，垃圾分类的相关研究主要从影响因素、回收模式、激励与约束机制3个方面展开：①关于垃圾分类的影响因素研究. 垃圾分类是一个复杂的系统工程，受多种因素的影响［6］，国内学者孟小燕［7］、谭爽［8］、曲英和朱庆华［9］分别探讨了居民垃圾分类的主观因素和外部情景因素、城市生活垃圾的政社合作的影响因素以及情境因素对垃圾分类行为的影响；国外学者Dijkgraaf 和Gradus［10］以及Thomas［11］认为激励与惩罚措施对垃圾分类效果具有显著影响. ②关于垃圾分类回收模式的研究. 娄成武［12］以政策网络为工具分析概括了德国、巴西和中国的垃圾回收网络，指出我国垃圾分类回收模式的回收力量分散、利益取向过于明显和责任归属不明确等问题；石超艺［13］以上海市梅陇三村为例，探讨了大都市社区生活垃圾治理推进模式，讨论了梅陇三村在垃圾分类标准、激励制度、推进主体创新、运行模式创新上的独特治理模式；姜建生等［14］深入剖析了国内外城市垃圾分类实践模式，结合深圳市为期6年多的试点试验，探索出了我国垃圾分类存在的问题. ③关于垃圾分类激励与约束机制的研究.国内外已有研究和实践表明，科学的激励机制对垃圾分类具有积极影响［15-16］；黄文芳等［15］以上海居民生活垃圾源头分类为例，讨论垃圾源头分类减量的激励机制，提出以法律强制为根本、以小区为单位，多种激励并重的激励机制；邹鹏［17］构建了城市生活垃圾资源化体系，并从经济激励、市场驱动机制、政策推动机制建立了激励机制，从减量回收机制、惩戒处罚机制、监督考评机制进行了约束和限制；Iyer和Kashyap［18］进一步论证了激励机制的时效性，认为激励政策效应会随着政策的截止而消失.

基于上述学者的相关研究可发现，当前关于垃圾分类的研究大多运用定性分析方法，定量研究较少［19］.随着博弈论方法的成熟，采用博弈论研究垃圾分类回收管理成为一大热点. 曹俊等［20］通过建立两阶段Stackberg动态博弈模型，讨论了垃圾发电厂如何制定利益分享合同条款，能促使消费者实行垃圾源头分类，提高垃圾燃烧热值，进而实现期望利润最大化. 叶健飞等［21］对城市垃圾分类回收的逆向物流监管机制进行了演化博弈分析. 张爽等［22］对政府、企业对低值可回收物处理中的演化过程进行了分析，并用六组数据进行仿真模拟. 此外，该学者还构建了居民垃圾分类行为和政府收费行为的演化博弈模型. 结果表明，居民垃圾分类行为与环保意识和政府收费政策有关，并指出政府制定合理的垃圾收费政策、加强宣传可引导居民参与垃圾分类［19］.

现有关于垃圾分类的博弈研究中，涉及的博弈主体大多是居民、企业或政府，对大学生和高等院校这一特定群体进行博弈分析的较少. 仅有李达［3］以高校和大学生作为研究对象，并在博弈模型中引入声誉资本，研究结果显示声誉损失对学生分类行为具有显著影响，但遗憾的是没有进行仿真分析. 本文借鉴以往学者的研究，以校园垃圾分类为研究对象，分析了大学生垃圾分类行为与高校监管行为，构建了两者的演化博弈模型，并用Matlab 2018a软件进行仿真分析，更清晰直观地展现了学生垃圾分类行为与学校监管行为之间的博弈过程，以探索垃圾分类政策如何更好地在高校校园中实施，为校园垃圾处理问题提供了理论上的支撑.

1 高校垃圾分类的博弈主体分析

高等院校的校园生活垃圾分类管理涉及多个主体，其中大学生是校园垃圾的主要制造者，也是校园垃圾源头分类的主要推动者. 现有文献中，大多认为大学生环保意识薄弱，不愿进行垃圾分类. 如赵雪［23］认为，大学生垃圾回收及循环利用意识不强，大多数学生放弃可再次利用的垃圾资源. 但也有学者对大学生环保意识进行了实证调查，结果表明88.9%的大学生对限塑令持支持态度，57.1%的大学生认为学生义务参加环保活动很有必要［24］. 可见，一半以上的大学生已经具备基本的环境素养，并非只考虑自身利益，不属于完全经济人. 所以，不能简单地对大学生进行经济人假设，部分大学生（以下简称“学生”）属于“有限理性社会人”，他们愿意为社会效益和可持续发展承担一定的责任. 计划行为理论认为，行为意向是影响行为的决定性因素，行为意向反过来受态度、主观规范和知觉行为的影响［25］. 在强制垃圾分类的时代下，当周围的同学朋友都进行垃圾分类时，受到社会规范和主观规范的影响，学生考虑到个人声誉，若不进行垃圾分类则会有声誉损失.

高校垃圾分类回收的监管主体主要是学校相关部门或者学生组织（以下简称“学校”），如学生会、研究生会、后勤部门等［3］. 高校垃圾分类的监管主体比较单一，不存在多层级管理制度，容易开展监管工作，不易使管理策略成为纸上谈兵. 因此，与其他居民和社区相比，高校校园在垃圾分类监管上具有一定的优势.

2 高校垃圾分类的演化博弈模型

2.1 模型假设与构建

假设1：高校校园垃圾分类的博弈主体为学生和学校，且两者都是有限理性的.

假设2：学生的行为策略集为｛分类，不分类｝，学校的行为策略集为｛监管，不监管｝.

假设3：学生选择分类的概率为x，选择不分类的概率为1-x；学校选择监管的概率为y，学校选择不监管的概率为1-y.

假设4：如果学生选择分类，则需要投入时间和精力成本C1，同时会因垃圾分类而获得生活环境提升的正效应R1，包括舒适的居住环境和有利于身体健康的潜在因素的影响. 同时，学生进行垃圾分类时，校园环境会得到提升，给学校带来正效应R3.

假设5：学校的监管成本为C2，包括人力、物力及财力成本等. 学校选择监管时，学校给予进行垃圾分类的学生奖励R2，包括德育成绩加分、评优评先评奖学金等. 学生不进行垃圾分类则会受到学校的处罚P，包括相应罚款、德育成绩扣分、劳动教育等.

假设6：学生的行为策略选择受到主观规范的影响，学生会考虑个人声誉，如果学生不进行垃圾分类，在社会规范和主观规范的约束下，学生的声誉受到损失f1. 同时，在当地政府强制垃圾分类政策的监管下，学生不分类则需要学校自行分类，导致学校处理校园垃圾的逆向物流成本增加，给学校带来负效应f2.

假设7：以上假设中所有参数均为正数.

根据上述假设及参数设计，构建学生和学校在不同策略下的收益矩阵，如表1.

2.2 模型分析

由演化博弈相关理论，易得学生采取分类策略和不分类策略的期望收益分别为：

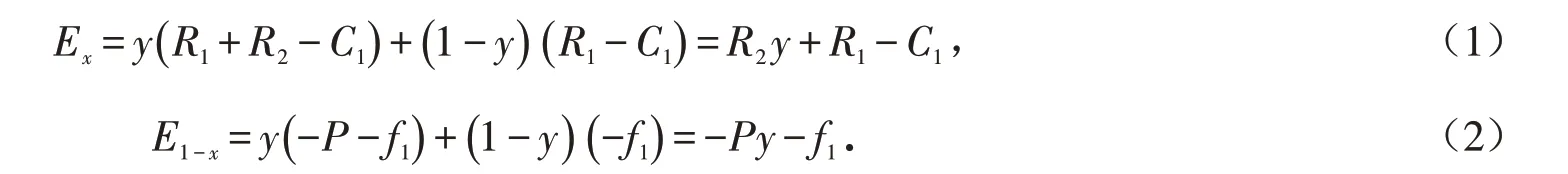
学生混合策略的平均期望收益为：

学生行为策略的复制动态方程为：

同理，学校采取监管策略和不监管策略的期望收益分别为：

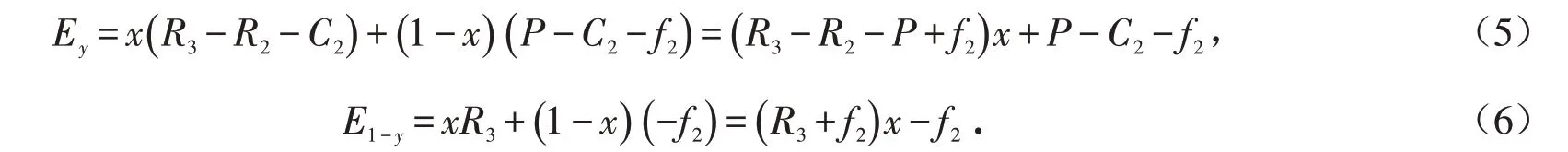
学校混合策略的平均期望收益为：

学校行为策略的复制动态方程为：

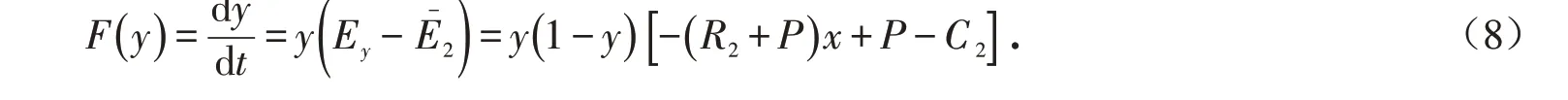
根据演化博弈的性质可知，上述5个平衡点的局部稳定性可由该系统对应的雅克比矩阵行列式和迹的值来确定，当且仅当detJ＞0，trJ＜0 时，平衡点具有稳定性. 由复制动态方程式（4）和（8）可知，该演化博弈模型的雅克比矩阵为：

将该系统中5个平衡点带入雅克比矩阵J中，并求得各个平衡点对应的雅克比矩阵行列式和迹的值，结果如表2所示.

表2 雅克比矩阵的行列式和迹的值Tab.2 Determinants and traces values of the Jacobian matrix

2.3 平衡点的稳定性分析

经计算不难得出，平衡点（p*，q*）迹的值为0，不能满足trJ＜0，因此该局部平衡点不是ESS. 在平衡点（1，1）处，要使detJ＞0，只需C1-f1-R2-P-R1＞0，只需C1-f1＞R2+P+R1，则必有C1＞P+R1+f1，必有trJ＞0.因此，平衡点（1，1）处不能同时满足detJ＞0 且trJ＜0，故平衡点（1，1）也不可能成为ESS. 下面分析其他3个平衡点成为ESS的条件.

情形1：当C1-R1＜f1且P＞C2时，平衡点的局部稳定性如表3所示，（0，0）为不稳定点，（0，1）为鞍点，系统存在唯一演化稳定策略（1，0）.

表3 情形1条件下的稳定性分析Tab.3 Stability analysis under the condition 1

情形2：当C1-R1＜f1且P＜C2时，平衡点的局部稳定性如表4所示，（0，0）为鞍点，（0，1）为不稳定点，系统存在唯一演化稳定策略（1，0）.

表4 情形2条件下的稳定性分析Tab.4 Stability analysis under the condition 2

由情形1和情形2可知，不管P和C2的大小如何，只要满足C1-R1＜f1，存在唯一演化稳定策略（1，0）. 这表明不论学校对垃圾不分类学生的处罚P与学校监管付出的成本C2孰大孰小，只要当学生垃圾分类付出的成本C1与垃圾分类得到的环境效应R1之差小于学生不进行垃圾分类时的声誉损失f1时，学生的行为策略趋向于垃圾分类，学校的行为策略趋向于不监管. 此时，整个系统达到理想状态，即学校不监管，学生自觉进行垃圾分类.

情形3：当C1-R1＞f1+R2+P且P＞C2时，平衡点局部稳定性如表5 所示，（0，0）和（1，0）为鞍点，系统存在唯一演化稳定策略（0，1）. 在此条件下必有C1-(R1+R2)＞f1+P，R1+R2是学校监管时学生进行垃圾分类获得的总的正效应，包括环境效应和学校给予的奖励；f1+P是学校监管时学生不进行垃圾分类学生获得的总的负效应，包括不分类的声誉损失和学校的处罚. 也就是说，当学生垃圾分类付出的成本C1与学生垃圾分类获得总的正效应R1+R2之差大于学生不分类获得总的负效应f1+P，且学校对学生的处罚P大于学校的监管成本C2时，学生的行为策略趋向于垃圾不分类，学校的行为策略趋向于监管.

表5 情形3条件下的稳定性分析Tab.5 Stability analysis under the condition 3

情形4：当f1＜C1-R1＜f1+R2+P且P＜C2时，平衡点局部稳定性如表6所示，（0，1）为不稳定点，（1，0）为鞍点，系统存在唯一演化稳定策略（0，0）.

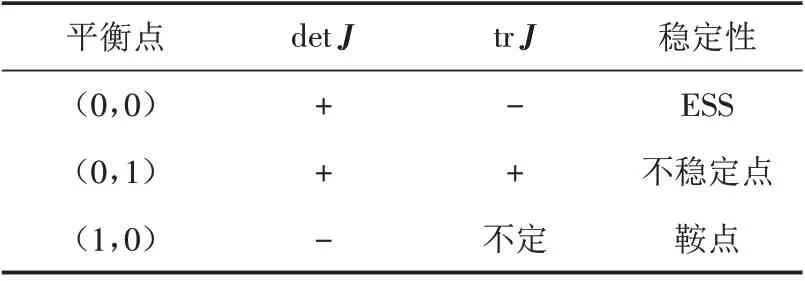
表6 情形4条件下的稳定性分析Tab.6 Stability analysis under the condition 4

情形5：当C1-R1＞f1+R2+P且P＜C2时，平衡点局部稳定性如表7 所示，（0，1）和（1，0）为鞍点，系统存在唯一演化稳定策略（0，0）.

表7 情形5条件下的稳定性分析Tab.7 Stability analysis under the condition 5

由情形4 和情形5 可知：当C1-R1＞f1且P＜C2时，即学生垃圾分类付出的成本C1与学生垃圾分类获得的环境效应R1之差大于学生不分类的声誉损失f1，且学校对学生的处罚P小于学校的监管成本C2时，学生的行为策略趋向于不分类，学校的行为策略趋向于不监管. 此时，垃圾分类政策在校园中很难实行下去，学校不能为社会其他组织树立榜样.

情形6：当f1＜C1-R1＜f1+R2+P且P＞C2时，平衡点局部稳定性如表8所示，平衡点均不能同时满足detJ＞0，trJ＜0，故不存在演化稳定策略ESS. 当学生垃圾分类付出的成本C1与学生垃圾分类获得的环境效应R1之差介于学生不分类的声誉损失f1和学生分类所获得总的正效应R1+R2与学校对不分类的学生的处罚P的和之间，且学校对不分类的学生的处罚P大于学校监管成本C2时，学生与学校的行为选择都无法趋向于一个稳定状态，整个系统处于震荡状态.

表8 情形6条件下的稳定性分析Tab.8 Stability analysis under the condition 6

综合以上所有情况，将不同条件下的ESS总结如表9所示.

3 仿真分析

本文对学生垃圾分类行为和学校监管行为的博弈过程进行了理论分析，为探究满足不同参数条件下学生和学校的博弈过程，并更直观地展现演化路径，采用Matlab 2018a软件对学生和学校之间的演化博弈模型进行仿真分析. 根据表9的结果，通过对参数C1、R1、f1、C2、R2和P的不同取值，验证上述博弈过程的演化稳定策略.

表9 平衡点成为ESS的条件Tab.9 The condition for the equilibrium point to be ESS

图1 描述了各参数满足C1-R1＜f1时系统的演化趋势. 设定参数值为C1=4，R1=2，f1=3，C2=5，R2=1，P=4，分别取x，y的初始值为（0.2，0.8）、（0.6，0.4）. 结果表明，无论学生和学校选择各自策略的初始概率如何，都将演化为学生进行垃圾分类，学校不监管. 只要满足C1-R1＜f1系统最终趋于理想状态，即学生在学校不监管的条件下自觉进行垃圾分类，此时垃圾分类政策更容易在高校校园内展开. 该理想状态下的行为选择策略仅与参数C1，R1，f1有关，与C2，R2，P均无关，可见，学生垃圾分类成本C1、垃圾分类给学生带来的环境正效应R1和学生不进行垃圾分类的声誉损失f1，对垃圾分类政策在校园内的实施起着关键作用.

图1 C1-R1 ＜f1 时的演化结果Fig.1 Evolution results under the conditions of C1-R1 ＜f1

图2 描述了各参数满足C1-R1＞f1+R2+P，P＞C2时系统的演化趋势. 设定参数值C1=8，R1=1，f1=1，C2=3，R2=1，P=4，分别取x，y的初始值为（0.2，0.8）、（0.6，0.4）. 结果表明，无论学生和学校选择各自策略的初始概率如何，都将演化为学生不进行垃圾分类，学校监管. 从图2可以看出，当学生与学校的初始概率分别为0.6和0.4时，学校的行为选择概率先降低后增加，最终趋于1（监管）.

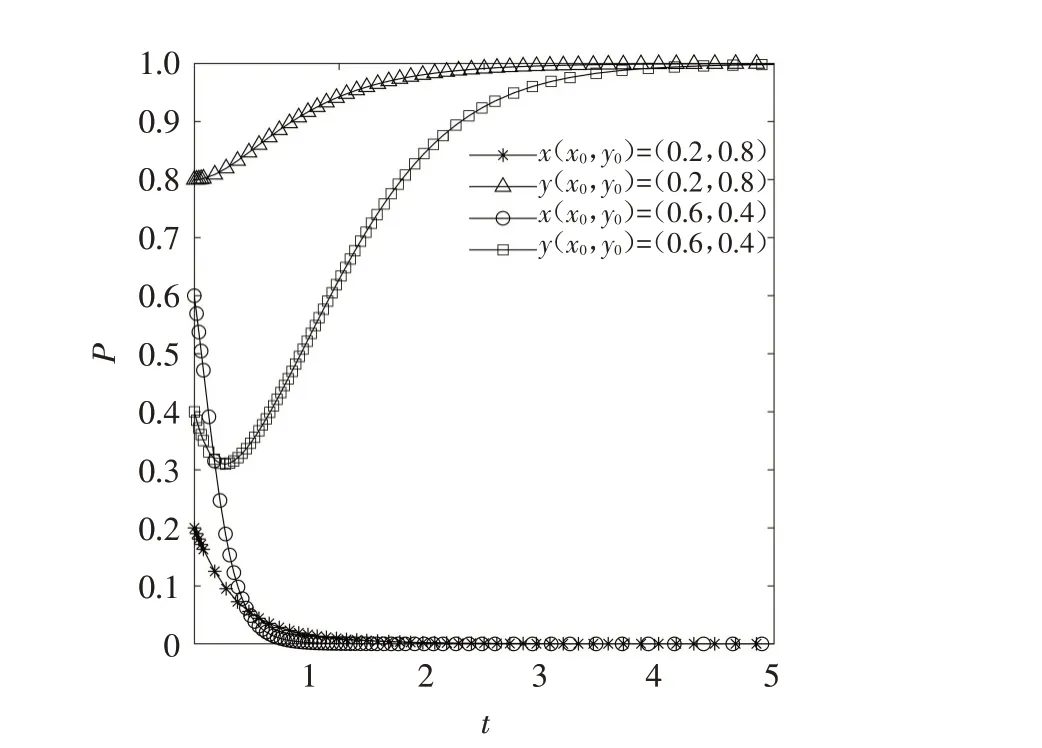
图2 C1-R1 ＞f1+R2+P，P ＞C2 时的演化结果Fig.2 Evolution results under the conditions of C1-R1 ＞f1+R2+P，P ＞C2

图3 描述了各参数满足C1-R1＞f1，P＜C2时系统的演化趋势. 设定参数值C1=5，R1=1，f1=2，C2=5，R2=1，P=4，分别取x，y的初始值为（0.2，0.8）、（0.6，0.4）. 结果表明，无论学生和学校选择各自策略的初始概率如何，都将演化为学生不进行垃圾分类，学校不监管. 从图3 可以看出，当学生与学校的初始概率为（0.2，0.8）、（0.6，0.4）时，学生的行为选择概率先增加后降低，最终趋于0（不分类）.

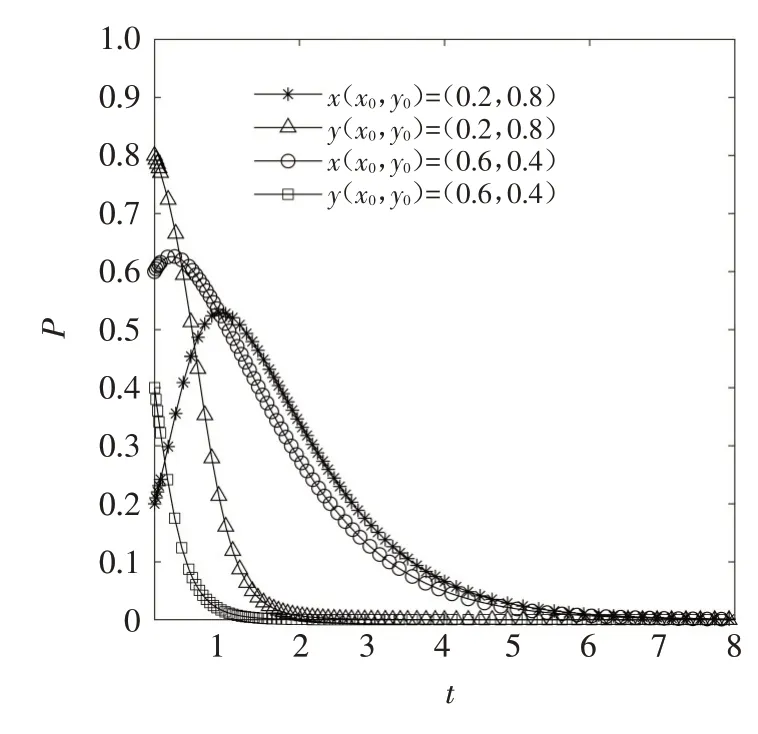
图3 C1-R1 ＞f1，P ＜C2 时的演化结果Fig.3 Evolution results under the conditions of C1-R1 ＞f1，P ＜C2

图4 描述了各参数满足f1＜C1-R1＜f1+R2+P，P＞C2时系统的演化趋势. 设定参数值C1=8，R1=3，f1=1，C2=3，R2=2，P=4，分别取x和y的初始值为（0.2，0.8）和（0.6，0.4）. 结果表明，学生和学校的行为选择都无法趋于某一稳定点，整个系统处于周期震荡状态.

图4 f1 ＜C1-R1 ＜f1+R2+P，P ＞C2 时的演化结果Fig.4 Evolution results under the conditions of f1 ＜C1-R1 ＜f1+R2+P，P ＞C2

4 结论与建议

4.1 研究结论

在强制垃圾分类的背景下，本文利用演化博弈工具对大学生垃圾分类行为与高校监管行为的演化博弈过程进行了研究，理论分析了演化稳定策略，并对演化博弈模型进行了数值仿真实验，得出以下结论：

1）学生垃圾分类行为与学校监管行为因素有关：学生垃圾分类付出的成本C1，学生进行垃圾分类给自身带来的环境效应R1，学生不进行垃圾分类的声誉损失f1，学校的监管成本C2，学校对进行垃圾分类的学生的奖励R2，学校对不进行垃圾分类的学生的处罚P.

2）当学生环保意识提高到一定程度，即R1＞C1-f1时，不管学校监管成本C2与学校对不进行垃圾分类的学生的处罚P大小如何，该模型存在唯一的演化稳定策略（分类，不监管）. 该状态下学校不监管，学生自觉进行垃圾分类，利于垃圾分类政策在校园内顺利开展.

3）当C1＞f1+R1，即学生进行垃圾分类付出的成本C1大于学生不进行垃圾分类受到的声誉损失f1与进行垃圾分类获得的环境效应R1之和时，不管学校监不监管，学生最终都不会选择垃圾分类.

4）当学生进行垃圾分类付出的成本C1∈[ ]f1-R1,f1+R2-R1+P，同时学校的监管成本C2小于学校对不进行垃圾分类的学生的处罚P时，学生和学校的行为选择都不能趋向于一个稳定状态，整个系统处于周期震荡状态.

4.2 政策建议

基于以上大学生垃圾分类行为与高校监管行为的演化博弈结果，为使垃圾分类政策在高校校园顺利展开，为社会其他部门树立榜样，提出如下建议：

1）在垃圾分类政策实施初期，高校应建立科学合理的监管机制来促使学生进行垃圾分类，有利于实现垃圾减量化和资源化. 但是，仅靠学校的奖惩制度不能使垃圾分类政策在高校校园内长久地实施下去，想要使系统长期趋于理想状态（分类，不监管），要降低学生进行垃圾分类付出的成本C1，提升学生垃圾分类时给自身带来的环境效应R1以及提高学生因不进行垃圾分类而受到的声誉损失f1.

2）加强垃圾分类的宣传工作，提高大学生进行垃圾分类带来的环境正效应R1. 高校及政府应不断强调垃圾分类对生态环境的积极影响，可以通过建立大学生社团组织、张贴海报、举办垃圾分类公益活动等方法宣传垃圾分类带来的好处，逐步增强学生的环境责任感和环保意识，带动社会居民自觉参与垃圾分类.

3）完善垃圾分类的基础设施，降低学生垃圾分类成本C1. 可以在高校校园中增加分类垃圾桶的摆放量、合理设置分类垃圾桶的摆放位置及距离，方便学生垃圾分类投放；向学生分发垃圾分类操作方法手册，加大垃圾分类的相关知识培训和操作指南的宣传力度，使学生快速掌握垃圾分类操作方法，从而降低学生垃圾分类的成本.

第四，建立高校校园垃圾分类信息披露制度，增强声誉损失f1对学生垃圾分类行为的约束力. 高校可以运用自媒体（微博、微信公众号等）开设校园垃圾分类专栏，对垃圾分类工作表现优异的班级或宿舍提出表扬，对垃圾分类工作表现较差的班级或宿舍提出批评，达到强化声誉机制的目的.