基于Copula方法的P2P区域风险传染研究

杨建辉， 黎绮熳， 谢永通

（华南理工大学工商管理学院，广州 510640）

P2P网贷行业经历了野蛮生长到监管整治，我国各地自2016年至今均出现不同程度的P2P行业爆雷现象，截至2019年底. P2P平台数量已经由最高峰时6608家锐减至343家. P2P作为完善我国金融体系的重要一环，始终备受学术界关注. P2P作为新兴的互联网金融业态，在区域之间是否存在风险传染问题，是基于什么样的风险传染机制，风险积聚是否会引发系统性金融风险的产生等问题一直备受关注. 但对于风险传染研究方面目前大多停留在定性描述层面. 本文在借鉴传统金融风险传染研究的基础上，结合互联网金融特征，引入Copula方法分析网贷行业内风险传染的相依结构，研究P2P区域间风险传染现象，进一步推动互联网金融的健康有序发展，也为金融监管部门制定行之有效的风险防控机制、防范区域风险扩大至系统性风险提供一定的参考.

1 Copula方法概述

1.1 Copula函数定义与性质

1.2 Copula方法与相关性测度

1.3 Copula模型的估计

1.4 Copula模型的评价方法

1.4.1 K-S检验和P-P图 K-S检验［13-14］和P-P图主要对变量的边际分布进行检验与拟合度评价.

K-S检验（Kolmogorov-Smirnov）方法原假设为实际分布函数与假定分布函数间无异，通过测定二者偏差的检验统计量进行检验. 这是一类常用的非参数检验方法，用于检验单一样本是否服从某一特定分布或多个独立样本是否服从同一分布. 对于Copula函数，当原序列进行概率变换后，理应服从独立同分布的（0，1）均匀分布. 于是可利用K-S检验，从而可对模型的边际分布假设进行检验.

P-P图可以直观地将拟合情况表现出来，根据变量的累积比例和指定分布的累积比例关系，若图示表现出一条直线，说明拟合情况良好，该指定分布拟合度优良. 否则，需对指定分布进一步变换改进.

2 风险传染的定义与测度

2.1 风险传染的定义

对于何为“风险传染”，学术界一直存在不同的定义.

国外学者根据形态表征定义风险传染. Forbes和Rigobon指出“相互关联性”是任何时期都客观存在的，在特殊危机时期表现出来的跨市场相关性显著增加的现象才是传染［15］. Karolyi再进一步将理性投资行为剔除出来，认为传染应该是非理性的风险传播［16］.

国内学者王献东和何建敏强调风险的传导渠道，将其分为实质性关联和非实质性关联，分别指贸易、金融等基本面联系和投资者行为、信息不对称等非基本面联系. 进一步将传染定义为由冲击产生的单个或多个金融市场风险通过金融市场间实质性关联渠道或非实质性关联渠道，导致其他市场出现风险的现象［17］.刘磊等利用CCA方法对我国金融风险传染进行分析发现当前宏观金融网络有利于部门间风险的分散，居民部门在网络中吸收了一定的风险［18］.

目前为止，学术界对传染的界定仍没有一致意见，这不便于对风险传染机制及测度的进一步研究，且学术界对风险传染多围绕传统金融在不同国家不同市场间的关联性进行定义，尚未有学者对于互联网金融行业或P2P网贷行业的风险传染现象进行定义. 借鉴田业钧对信用风险传染的研究［19］，本文将P2P网贷风险传染界定描述为：单个或多个P2P网贷平台风险事件爆发，通过平台间的关联，导致局部或大范围内的平台出现风险事件的现象.

2.2 风险传染的测度

风险传染的多种定义使得学术界产生了多种对风险传染进行测度的方法，这些方法有相关系数方法、GARCH簇模型［20］和Copula方法［21］等.

2.2.1 相关系数方法 相关系数法考察不同金融市场中的不同变量之间的相关系数变化. 当原本稳定的相关系数，随着金融危机的产生而显著性增加，则说明产生了传染现象. 这种方法存在较大缺陷，因为相关系数是不适用于非线性变化情况的，而这种非线性情况又广泛存在于各种金融资产之间. 此外Forbes和Rigobon指出市场收益存在异方差性，传统的相关系数方法检验是有偏的. 过于简化金融市场变量间的相关关系和严格的假设条件，使得相关系数方法存在严重缺陷.

2.2.2 GARCH簇模型方法 GARCH簇模型方法重点关注波动溢出的估计，以此描述资产价格二阶矩的跨市场运动，此后的研究在GARCH模型基础上拓展出多种不同的组合模型，其中VAR模型方法结合GARCH模型用于检验风险传染最为普遍. 众多的实证检验证明GARCH模型能更好地刻画波动的动态相关及风险传染，但缺陷在于波动持续性可能被高估，当市场处于下跌时期，运用GARCH 模型会预测出较上涨时更高的波动性.

2.2.3 Copula方法 Copula理论最早由Sklar在数理统计领域中提出，可用于多变量的联合分布分解后描述变量的相关性［22］，也被称为“连接函数”［23］. Copula函数能描述非线性、非对称性和尾部相关性，且无须对模型做严格的假设，因此用以刻画风险传染和金融变量间的相依结构具有良好的性质. Copula方法的优点表现为可刻画非线性相关关系、非对称关系以及尾部相关关系等，已被广泛应用到金融危机风险传染的实证研究当中. 本文尝试将Copula函数应用于P2P网贷行业当中. P2P网络借贷风险管理的一大核心问题是对平台间风险相关性的刻画，这可能直接导致整个行业的危机产生. 借助Copula函数的良好性质可以更好地描述市场中的相依结构，从而反映出P2P网络借贷的风险传染.

3 基于Copula方法的P2P网贷相依结构模型构建

利用两阶段方法构建Copula模型，具体分为：第一步，确定各单变量的边际分布模型；第二步，选择适当的Copula函数拟合. 这样就将各变量自身的分布与变量间的相依结构分开，实现分离研究. 在P2P网络借贷平台风险传染研究中，可对每个变量确定各自的边际分布，再通过Copula 函数刻画平台间相关数据的相依结构.

对于P2P网络借贷风险传染相关结构的建模，步骤如下.

1）样本选择. 选择能反映P2P 网络借贷风险传染的相关数据，经过预处理得到样本数据，进行描述性统计分析. P2P 网络借贷行业的风险传染表现有两个特点：一是传染表现在量价关系中，即交易数和成交利率的波动能反映市场中风险传染的强弱程度. 二是同一地区市场内会出现大面积的风险事件，对于不同地域市场间的风险传染现象需要进一步刻画. 鉴于此，本文选择六个地区市场的日交易额数据进行两两建模分析. 首先对数化处理数据，得到样本数据. 接着对样本数据进行描述性统计分析，得到样本数据的边际分布特点.

2）确定边际分布. 根据描述性统计分析，P2P 网贷市场表现出一定的“尖峰厚尾”（Leptokurtosis）特征，这类似于多数金融序列. 由于检验发现变量拒绝服从正态分布，分布函数难以用现有的模型进行拟合，因此借鉴已有文献的处理办法，利用样本的经验分布函数近似为边际分布函数［24］.

3）选择合适的Copula函数. 根据变量间的联合分布频数直方图和频率直方图展现的图像特征，结合常用Copula 函数的图像和性质，初步选择出备选Copula 函数. 其中，常用的函数形式包括椭圆连接函数和阿基米德连接函数.

4）模型参数估计. 对指定的备选Copula的参数进行估计，得到对应的Copula模型. 估计方式选择半参数估计法，通过经验分布函数的估计值代入Copula函数进行参数估计.

5）模型评价. 计算各模型拟合下的平方欧氏距离，通过距离大小比较拟合效果，做出最优拟合Copula模型的选择.

6）相关性分析. 完成以上五步，已得出P2P网贷市场中的相依结构. 此时通过计算相关系数——各秩相关系数和尾部相关系数，进一步对相关结构中的一致性相关、线性相关、尾部相关做出描述.

4 实证分析

4.1 数据选取与预处理

本文选取由深圳市电子商务协会发布的“中国P2P网贷发展指数”作为原始数据（在第一网贷网站查询http：//www.qcqs.com.cn）.“发展指数”的本质是已纳入统计的平台每日交易额. 选用此指数的理由在于交易数和成交利率的波动能一定程度上较好地反映市场中风险传染的强弱程度. 当市场出现风险事件时，往往造成投资者的恐慌心理蔓延，使得交易额出现较大的波动［25］.

选取发展较快且具备典型性的5个区域或城市的网贷“发展指数”进行分析，分别为北京指数（以下简称“京指”）、上海指数（以下简称“沪指”）、广东指数（以下简称“粤指”）、浙江指数（以下简称“浙指”）以及深圳指数（以下简称“深指”）. 其中，鉴于深圳是全国P2P网络借贷最具活力的城市，因此单独于广东进行分析，保留剔除深圳数据的广东指数（以下简称“粤（除深）”）. 考虑到两年P2P由于监管加压处于低迷期，处于低风险水平，因此本文数据时间选取P2P网贷交易活跃期，从2015年5月7日至2017年4月24日，剔除期间内节假日等不交易的时间，得到数据共计4152条.

根据“发展指数”的计算方式，可知发展指数为统计平台的综合加权交易额，计算方式如

其中，设P2P借贷交易市场中，Mi表示标的本金，Qi表示该标的期限.

进一步预处理上述二手数据，得到对数化发展指数（下文简称“指数”）：

4.2 描述性统计分析

表1分别从指标数据反映P2P网贷不同市场的对数发展指数的基本统计特征. 从直方图和偏度、峰度指标来看，各个区域市场均存在“尖峰”和“厚尾”特点. 从均值来看，各个市场均值都为正数，反映了市场交易额整体走高的现象；从偏度系数来看，各市场均大于零，粤指与深指的分布较为对称，而京指、沪指和浙指分布稍微右偏，厚尾存在于右侧；从峰度来看，均大于3，较正态分布更加陡峭，反映了市场交易额变动的中心聚集程度较高；从J-B检验P值可判定各序列均拒绝服从正态分布的假设，可见各序列服从某种尖峰厚尾的分布.

表1 各地区指数的描述性统计基本指标Tab.1 Basic indicators of descriptive statistics of regional indexes

4.3 模型构建与分析

4.3.1 边际分布模型的确定 由描述性统计可知，随机变量服从某种尖峰厚尾分布，总体的分布不易确定，因此采用基于经验分布确定边际分布模型的方法，即用样本的经验分布函数近似作为随机变量的分布函数. 鉴于篇幅限制，接下来的研究将选取京指与深指（对应序列X，Y）的建模分析为例进行说明. 利用Matlab软件求得X和Y的经验分布函数U1与V1，进一步绘制经验分布函数如图1所示.

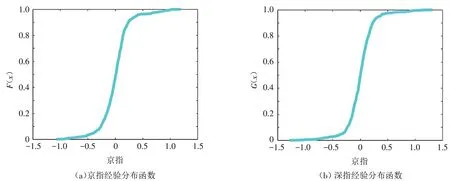
图1 京指与深指的经验分布函数图Fig.1 Plot of empirical distribution functions of Beijing index and Shenzhen index

4.3.2 Copula函数的选择及估计 通过经验分布函数近似确定了X和Y的边际分布U=F(x)和V=G(x)后，由于函数形式难以写出，因此利用图像进行判断. 据此使用软件做出(Ui,Vi)(i=1,2,…,n)的二元频数直方图（即连接函数图像）和二元频率直方图（即连接密度函数图像），如图2所示. 根据图像以便从直观角度观察并选取合适的Copula函数类型进行进一步的拟合.

从图2看出，京指与深指二元相依结构的图像具有一定的对称性，结合常用二元Copula函数的性质，选取正态连接函数和t连接函数比对用以刻画京指与深指的相依结构.

图2 京指与深指的连接函数与连接密度函数图Fig.2 The graph of the connection function and connection density function of Beijing index and Shenzhen index

对参数进行估计，结果如表2.

表2 不同Copula函数的参数估计Tab.2 Parameter estimation of different Copula functions

将参数的估计值ρˆnorm、ρˆt、φˆ分别代入两个连接函数的表达式中，得到拟合的二元正态Copula函数的分布为：

拟合的二元t-Copula函数分布为：

得到Copula的参数估计后，为从直观上理解，进一步利用软件画出对应的密度函数图并着以不同颜色，同时画出连接函数的分布函数图.

由图3、图4 可以直观看出，拟合的Copula 函数模型能对称刻画指数间的相依结构，进一步对比可知，t-Copula函数能较好地反映京指与深指的相依结构.

图3 拟合的正态连接密度函数和分布函数Fig.3 Fitted normal connection density function and distribution function

图4 拟合的t连接密度函数和分布函数Fig.4 Fitted t-connection density function and distribution function

4.4 模型评价与相关性分析

根据式（13）可以计算出拟合连接函数与经验连接函数的平方欧氏距离，结果如下：

由此进一步认为二元t-Copula模型（ρˆt=0.266 6，kˆ=3）对京、深指数情况观测数据有较好的拟合效果.

根据公式（2），（4）～（6）分别计算秩相关系数和尾部相关系数，从而通过相关系数反映京指与深指的相依结构，结果如表3所示.

表3 京指与深指的相关系数对比Tab.3 Comparison of correlation coefficients between Beijing index and Shenzhen index

对表3中经过显著性检验的各系数分析可知，从Kendall 秩相关系数值来看，京指与深指间存在显著的弱相关性，说明两个指数之间存在部分一致性变化，两个变量间有接近6成的变化是一致的；从Spearman秩相关系数来看，京指与深指间存在弱线性相关性；尾部相关系数由于不存在于0，1，因此认为京指与深指不存在显著的尾部相关性.

根据上述建模思路，对6个指数两两之间的相关结构进行建模，结果如表4所示.

表4 区域指数间相关结构的二元Copula建模Tab.4 Binary Copula modeling of correlation structure between regional indices

从Kendall秩相关系数来看，京指与沪指、粤指与沪指、沪指与深指、京指与浙指的秩相关系数都大约为0.09，可以说明，这几个相依市场间的变化基本上有一半是一致的. 其他几个市场间则大于0.13，由此说明这些市场间的一致性运动程度较前者高.

从Spearman 秩相关系数来看，京指与粤指、京指与深指最大，约为0.25，认为市场间有弱的线性相关关系. 浙指与粤指、深指与粤指（除深）、浙指与深指则次之，处于0.20左右，说明浙江作为民间借贷活跃的地区，影响范围较大，与广东市场存在一定的相关性.

从拟合的t-Copula函数参数来看，发现上海与其他地区指数间相关结构相似，而其他地区之间也相似，二者存在轻微差别. 另计算发现各个市场指数间不存在显著的尾部相关系数，可认为各区域市场间不存在显著的尾部相关性.

5 结论

本文通过Copula方法构建P2P网贷相依结构模型，选取发展较快且具备典型性的5个区域或城市的网贷“发展指数”进行实证分析，研究区域间P2P风险传染情况. 首先描述性统计分析表明不同区域P2P市场具有差异性，且每个地区的P2P网贷指数总体分布均呈现“尖峰”“厚尾”特点，与传统金融序列的分布特征类似；之后观察到经验分布函数、连接函数、连接分布函数图像可知，指数间存在一定的对称性，选择二元Copula函数，实证发现P2P两两市场变量间的相关结构可利用t-Copula模型较好地描述，二元t-Copula函数对相关变化敏感，可捕捉P2P借贷市场内不同区域市场间的非线性相关性. 最后通过两两区域指数间相关结构的二元Copula建模发现不同区域市场之间的Kendall秩相关系数和Spearman秩相关系数均处于0.1～0.3水平，为弱相关水平，而且不同区域市场之间不存在显著的尾部相关性，即不存在一个地区市场波动巨大，使得另一个或多个市场波动概率显著增加的波动溢出现象. 由上可知，不同于沪、深股市等较为成熟的金融市场，P2P网络借贷市场间的相关性不高，不同区域市场具有不同的风险特征，问题平台的风险跨区域传染不明显.