随机互联非线性系统的神经网络约束控制

祁 林，渠俊锋，司文杰

(1.河南城建学院 电气与控制工程学院，河南 平顶山 467036；2.国网许昌供电公司，河南 许昌 461000)

随着科技的快速发展，互联非线性系统越来越多地出现在各种实际系统中，如电力系统、经济系统、生态系统、计算机通信系统以及大型工业控制系统等[1-3]。互联非线性系统具有高阶性、强耦合、强不确定性等特点，传统的控制理论难以解决非线性互联系统的分析与设计问题[4]。许多互联非线性控制系统中需要考虑状态约束问题。与此同时，随机干扰在工程设计中不可避免，随机干扰的存在会导致运行越过安全边界使系统遭到破坏[5]，特别是对于不确定高阶非线性互联系统。很多研究人员针对高阶系统的稳定性和跟踪控制进行了广泛研究。文献[6]采用一种鲁棒自适应神经动态面跟踪控制方案，提高了严格反馈型不确定非线性系统的信号跟踪性能。文献[7]针对状态不可测且存在未知非线性项和扰动的切换非线性系统，设计了自适应反步滑模控制方案，实现了参考信号的快速跟踪，保证了被控对象的稳定性。另外，当实际系统受到约束影响时，通常采用BLF方法来实现自适应控制设计[8-10]。文献[11]提出了一种自适应模糊神经网络控制方案，该方案通过BLF约束机器人的运行范围。文献[12]通过利用迭代学习控制来考虑多输入多输出受限的非线性系统。但是，对于不确定的具有未知动态特性且受输出约束的高阶随机非线性互联系统，几乎没有跟踪控制的研究结果。

基于上述研究与分析，文章将针对受输出约束的高阶随机非线性互联系统提出一种分散自适应跟踪控制方案，利用RBF NN的逼近能力处理完全未知的非线性函数和随机干扰，采用BLF方法解决输出约束问题，采用Matlab仿真验证所提出控制方案的有效性。

1 被控系统模型及准备

1.1 互联非线性系统的建模

考虑以下不确定的高阶随机非线性互联系统，该系统模型可应用于电力、工业、生态等领域。

(1)

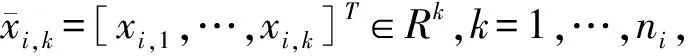
本文的输出约束控制器设计中，方程组(1)所描述的系统结构假定了高阶非线性和非线性互联作用是未知的，并且考虑了随机干扰。控制目标是构建分散自适应控制器，使所有闭环信号有界，可以驱动系统输出yi跟随有界的期望信号ydi，并且系统输出不能越出其约束范围。

|xp-yp|≤p|x-y||xp-1+yp-1|

|x+y|c≤2c-1(|x|c+|y|c)

(2)

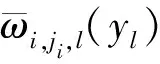
(3)

1.2 RBF神经网络

RBF神经网络具有局部逼近能力，可用于未知非线性系统控制器的设计[16]。在紧集内连续函数f(Z)为：

f(Z)=W*TS(Z)+(Z)

(4)

其中，Z∈ΩZ⊂Rq是神经网络输入。W*是最优神经网络权值矢量，(Z)是逼近误差，‖(Z)‖≤*.S(Z)=[s1(Z),s2(Z),…,sl(Z)]T是径向基函数，高斯函数形式为：

(5)

其中，ξi=[ξi1,ξi2,…,ξiq]T代表神经元中心，η是si(Z)的宽度。

最优神经网络权值矢量可表示为：

(6)

2 自适应控制设计

控制器设计用到了反步法和对未知系统函数的神经网络逼近。自适应控制器设计框图如图1所示。

图1 系统控制器设计框图

系统的输出与系统的参考轨迹进行对比，产生系统跟踪误差。在第一步中，由跟踪误差和自适应神经网络的逼近函数构造虚拟变量；设计过程中每步是迭代运算的，第二步中的虚拟变量是由系统状态和上一步的虚拟变量做差，与自适应神经网络的逼近函数构造，依次迭代，最终得出需要的控制器。具体理论推导分析如下：

给定pi=max{pi,ji,i=1,…,m,ji=1,…,ni}，满足pi,ji≥1为奇数，考虑以下坐标变换：

zi,1=yi-ydi,zi,ji=xi,ji-αi,ji-1,i=1,…,m,ji=2,…,ni.

(7)

其中，αi,ji-1是随后给出的虚拟控制量。

步骤i,1：考虑式(1),有

(8)

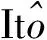
(9)

根据Young不等式,采用迭代计算可以得到：

(10)

虚拟控制量构造为：

(11)

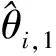
自适应参数更新为：

(12)

其中，σi,1>0是设计参数。

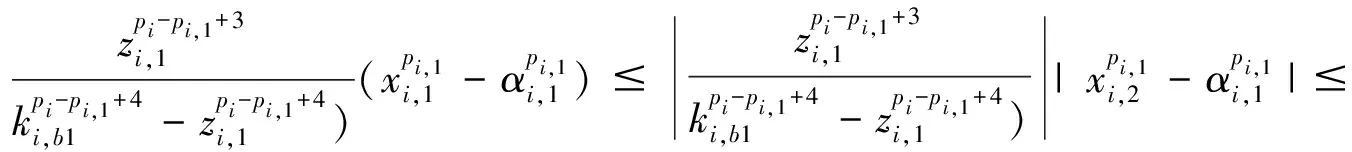
(13)

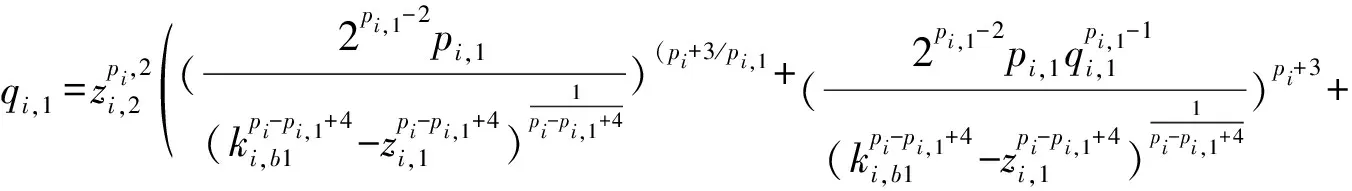
考虑式(13),式(10) 可重新整理为：

(14)

反步法推导过程中，需要进行迭代计算。在步骤i,ji(i=1,…,m;ji=2…ni-1)，类似上述步骤,在每步ji中过程均采用迭代计算。

步骤i,ni:zi,ni=xi,ni-αi,ni-1，直接给出自适应参数：

(15)

构造的控制器如下：

(16)

3 稳定性分析

(17)

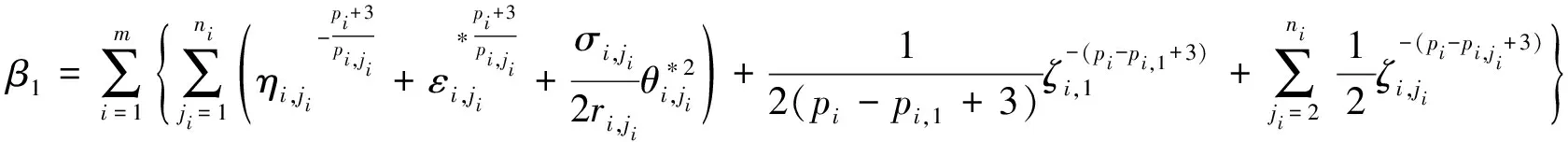
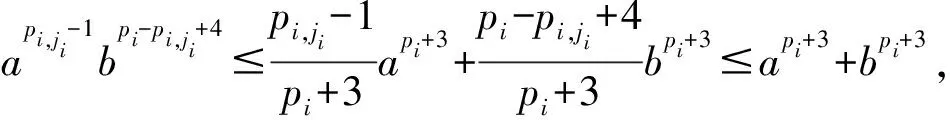
(18)

LV≤-α0V+β0

(19)

基于控制器式(16)，可得：

(20)

其中，E(V)代表了期望算子。对不等式 (20)求积分可得：

(21)

至此，验证了闭环系统中所有信号半全局一致最终有界。

通过以上分析，可得出以下定理：考虑非线性互联系统式(1)满足假设1～2，控制器式(16)和自适应参数式(12)和式(15)。得出在有界的初始条件下，能保证式(1)所有闭环信号都将有界；式(2)输出信号受限在预定的范围内；式(3)输出跟踪误差收敛到原点附近的一个小邻域中。

4 仿真研究

为了验证所提出的控制方案的有效性，利用MATLAB进行了控制系统仿真。

考虑以下随机互联非线性系统：

控制目标是设计一个控制器使得所有信号有界，y1和y2跟踪yd1=0.5sin(0.8t)+0.8cos(1.2t)和yd2=0.5cos(0.8t)+0.8sin(1.2t))。

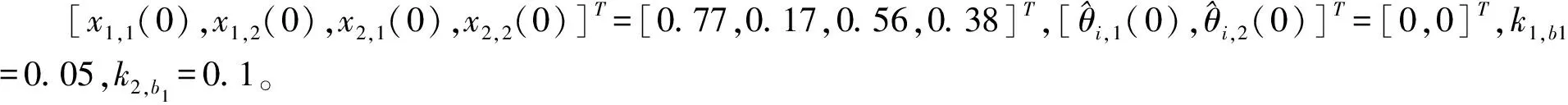
在仿真中，设计参数设定为：k1,1=28，k1,2=32，k2,1=26，k2,2=29，r1,1=r1,2=r2,1=r2,2=1,η1,1=η1,2=η2,1=η2,2=12，σ1,1=0.75，σ1,2=0.43，σ2,1=0.6，σ2,2=0.25。

仿真结果如图2～图10所示。

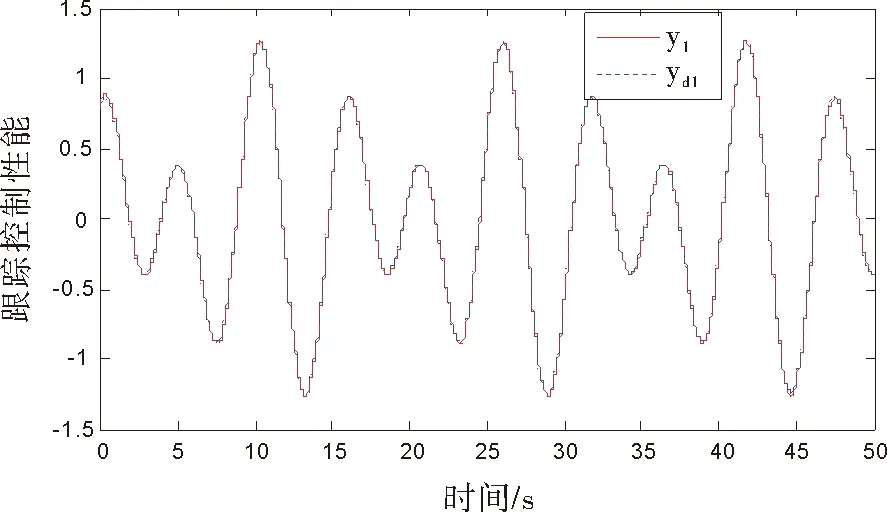
图2 系统输出y1和参考信号yd1

图3 系统输出y2和参考信号yd2

图2给出了子系统输出y1和系统跟踪轨迹yd1=0.5sin(0.8t)+0.8cos(1.2t)，该子系统的输出能很好地实现跟踪效果，完成了跟踪控制任务。图3给出了第二个子系统的输出y2和跟踪理想轨迹yd2=0.5cos(0.8t)+0.8sin(1.2t)，从图3中可以看出该子系统的输出完成了跟踪控制任务。

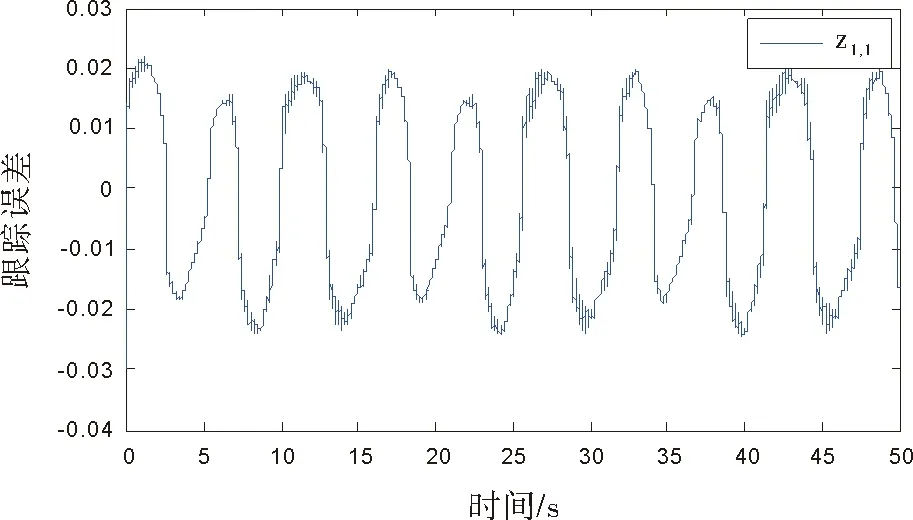
图4 跟踪误差z1,1

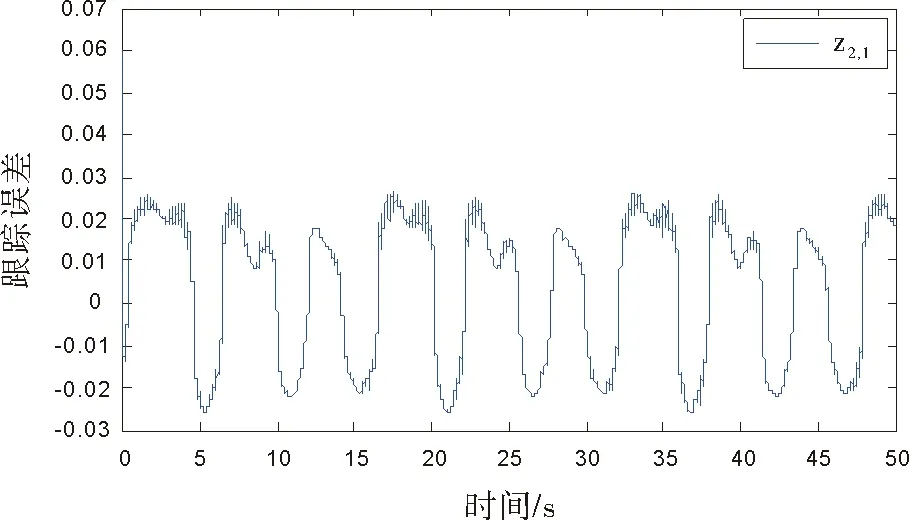
图5 跟踪误差z2,1

文中设计的是输出受限的跟踪控制，从图4中可以看出系统输出和参考轨迹的差值z1,1=y1-yd1，随着时间t增加跟踪误差能收敛到零值附近，误差z1,1最终收敛到0.03到-0.04之间，可以看出系统输出约束在设定的受限范围[0.05,-0.05]内。从图5中可以看出系统输出和参考轨迹的差值z2,1=y2-yd2，随着时间t增加跟踪误差z2,1能收敛到零值附近，从图5看出误差z2,1收敛到0.03到-0.03之间,系统输出约束在[0.1,-0.1]预定的范围内。

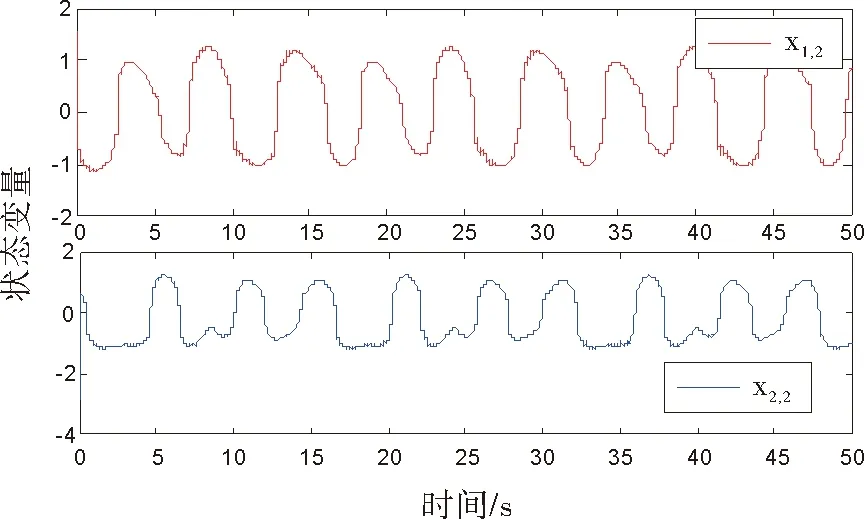
图6 系统状态x1,2和x2,2

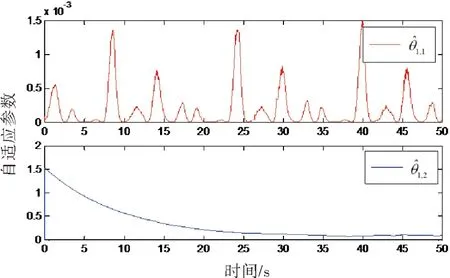
图7 自适应参数和

图8 自适应参数和

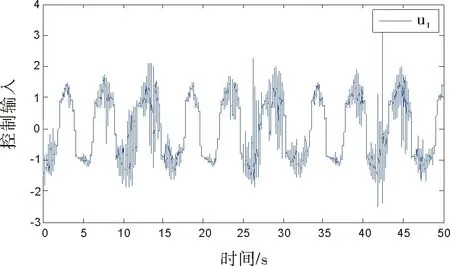
图9 控制输入u1

图10 控制输入u2

5 结论

针对受输出约束的高阶随机非线性互联系统，提出了一种分散自适应跟踪控制方案，利用RBF NN的逼近能力处理了完全未知的非线性函数和随机干扰，采用BLF方法解决了输出约束问题。主要优点是在输出受限控制中考虑了随机干扰，提出的控制方案只需要一个自适应参数即可估计，并且将RBF NN用作函数逼近器，克服了过参数化问题。同时，基于Lyapunov稳定性理论，证明了设计的控制器可以确保整个闭环系统中的所有信号都有界，并且跟踪误差收敛到零的小邻域，并通过Matlab仿真，证明了所提出方案的有效性。