基于概率统计的桥梁校验系数常值范围精细化研究
梁茜雪
(广西交科集团有限公司,广西 南宁530007)
校验系数是桥梁荷载试验评定最重要的指标之一,校验系数常值范围的精度直接决定桥梁承载力评定的可靠程度, 传统荷载试验评定中校验系数常值范围长期以来取值粗略而无法适应目前桥梁承载能力评定,使得传统荷载试验评定方法在承载力评价时存在错判、误判的风险。目前校验系数常值范围的研究方法主要包括按统计方法对多座桥梁的试验数据进行分析确定[1-10],或由校验系数主要影响因素的统计特征值确定[11],或引入校验系数影响因子确定[12]。由影响因素的统计特征值确定校验系数的方法因需要建立基本变量与综合变量间的数学表达式,目前仅适用简单结构,且多数影响因素的特征值也建立在经验和假设的前提下,故暂时无法用于实际检测中。校验系数影响因子的概念是由长安大学王凌波提出,将影响校验系数的因素分为3 类,对应得出3 个影响因子,并采用单位值1 与3 个因子极值之和进行阐述,但由于影响因子极值的取值没有可靠的依据,这种方法仍处于理论研究状态。 本文以大量预应力混凝土小箱梁校验系数实测值为统计样本,采用概率统计方法对桥梁承载能力评定的校验系数范围进行了研究,优化了统计样本的选取原则,提出了桥梁校验系数常值精细化范围,对桥梁荷载试验的发展与完善具有推动作用。
1 校验系数常值研究现状
近十余年来国内陆续开展了对空心板、T 梁、箱梁、拱桥、连续刚构、斜拉桥等桥型的校验系数常值范围统计分析,但鉴于校验系数的影响因素种类多,仅从某一大类桥型来确定常值范围,要求有足够的样本以涵盖各类因素的变化,才可反映总体的统计特征,而现有的研究采用的样本范围较窄、数量较少,未能给出科学的指导范围。 校验系数常值是在1988 年颁布的《公路旧桥承载能力鉴定方法(试行)》(以下简称《试行方法》)首先提出,方法中对4 大类桥型的应变和挠度校验系数常值范围做了规定。如表1 所示,现行常值范围按《公路桥梁荷载试验规程》(JTG/T J21-01-2015)(以下简称《试验规程》)选取,规程在《试行方法》的4 类桥型的基础上增加了2 类桥型的校验系数常值[13-16]。
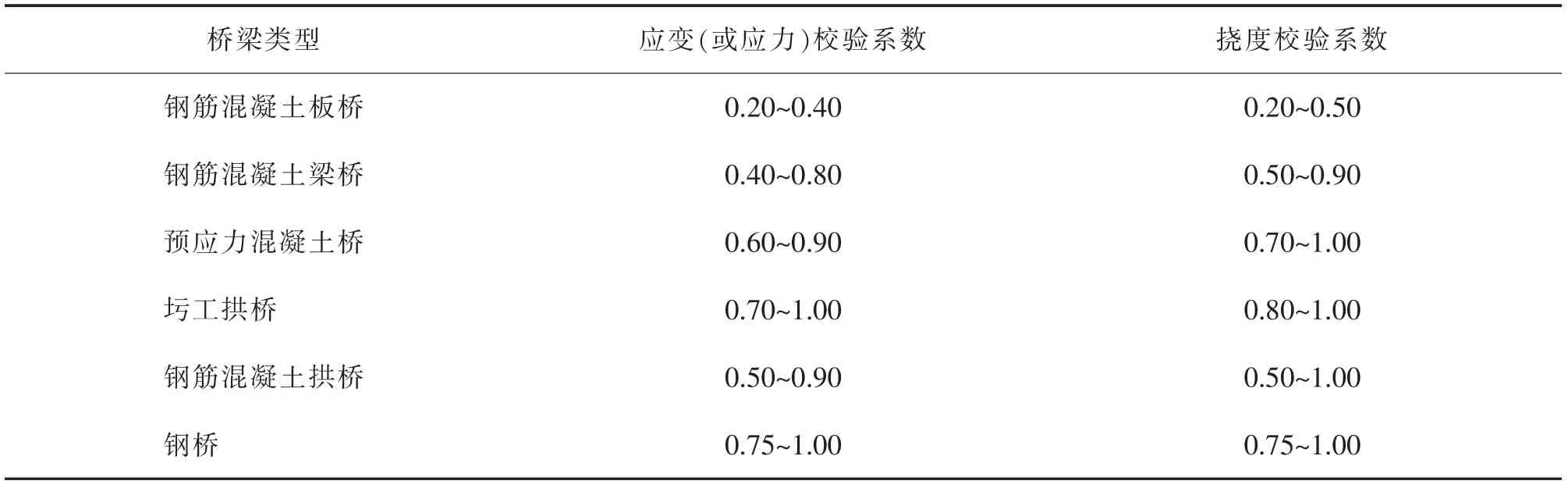
表1 常见桥梁结构试验校验系数常值表Tab.1 Testing coefficient of common bridge structure
2 校验系数常值确定方法
2.1 概率统计分析方法
采用数理统计方法进行校验系数常值范围研究的原理是将校验系数作为随机变量,通过对校验系数样本的分析得出总体的数字特征,由总体数字特征确定校验系数常值区间。 本文采用蒙特卡罗法(Monte Carlo Method),又称随机抽样法或统计试验法, 在目前结构特性的随机分析中,它被认为是一种相对精确的方法,分析方法流程图见图1。
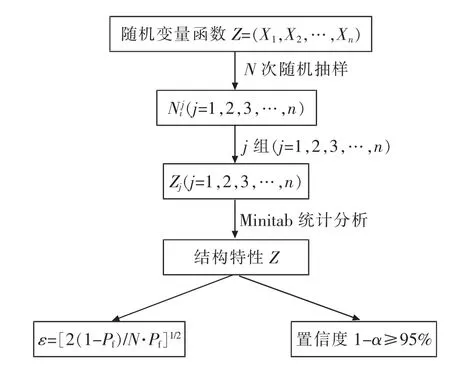
图1 蒙特卡罗分析方法流程图Fig.1 Flow chart of the Monte Carlo method
2.2 校验系数样本选取原则
通过设置样本选取原则,减少校验系数影响因素,同时在限定条件下,样本空间包含足够多其它因素影响的样本,误判风险明显下降。 根据此原则分别对校验系数影响较大的主要因素进行限定, 包括桥梁的施工及设计质量控制水平、测试截面位置和数量、结构分析方法、附属结构对刚度影响、试验加载方式及效率,本文样本选取的具体要求为:
1) 桥梁为近5 年广西高速公路新建预应力混凝土小箱梁桥;
2) 桥梁未发生施工质量事故,外观质量较好,承重构件无裂缝及较大缺损;
3) 桥梁测试截面位置和数量根据《试验规程》进行选定;
4) 结构分析采用梁格法建立有限元空间模型,考虑混凝土铺装层对结构刚度提高(扣除2 cm 混凝土铺装层厚度),但不计入沥青铺装及护栏影响;
5) 按照《试验规程》进行试验工况设计,且加载效率满足0.85~1.05。
3 校验系数常值精细化范围研究
3.1 校验系数样本
以预应力混凝土小箱梁桥为例进行校验系数常值精细化范围研究, 通过收集近5 年建成的11 条高速公路上77 座预应力混凝土小箱梁桥交工验收荷载试验数据作为样本。 按照最不利原则,以控制截面控制梁片的应变和挠度校验系数为主要研究对象,使用数理统计方法确定预应力混凝土小箱梁桥的应变和挠度校验系数常值范围。 进行统计分析前需剔除因测量误差、计算误差、环境影响等引起的疑似异常值。 本文采用拉依达准则进行异常值判别,认为[μ-3σ,μ+3σ]之外的数据为异常值,其中,最大正弯矩工况控制梁片应变和挠度异常值分别占样本总体的1.18%和0.07%,判别前后的样本参数见表2。
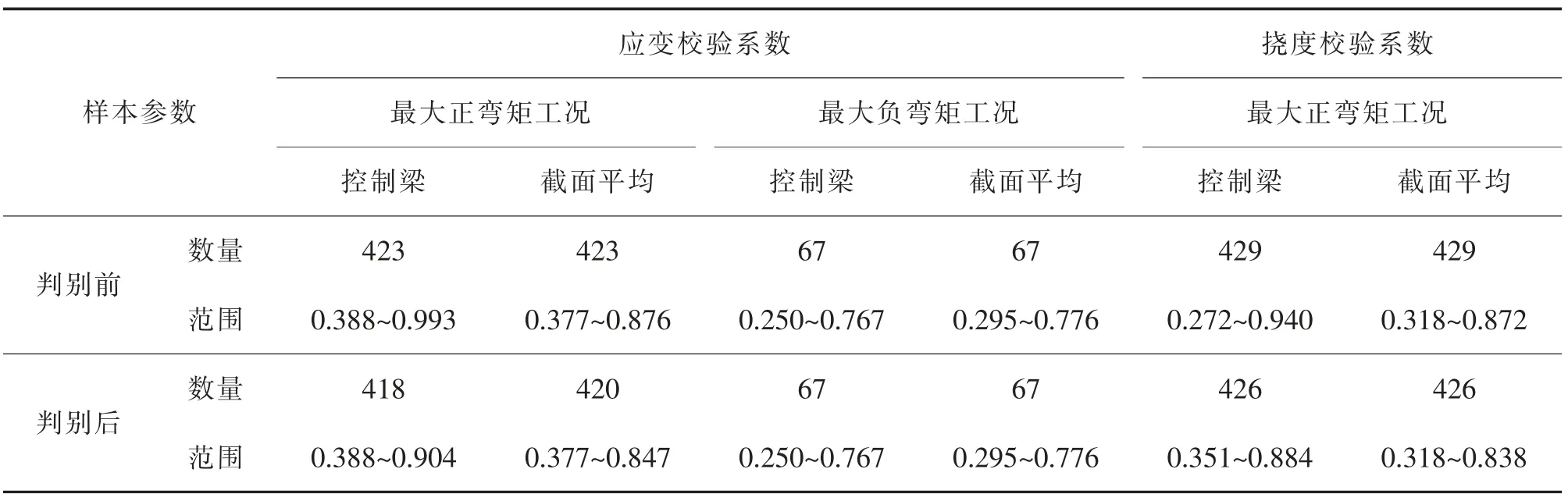
表2 校验系数样本参数表Tab.2 The sample parameters of testing coefficient
3.2 校验系数总体统计分析
选取的样本包含预应力混凝土小箱梁各种标准跨径,分别为20,25,30,35,40 m。 由于连续梁桥荷载试验时的最大正、负弯矩控制截面分别位于跨中和支点附近,截面布置和受力均不相同,为分析箱梁不同部位校验系数常值范围的差别,按最大正、负弯矩工况控制截面将校验系数分为两大类,在前述分类的基础上再细分为控制梁校验系数和截面平均校验系数(所在截面各片梁校验系数的平均值),以分析局部和整体校验系数是否存在不同。
采用统计软件Minitab 分析控制梁及截面平均应变和挠度校验系数样本。 首先对各组样本进行概率统计分析,限于文章篇幅,仅列出最大正弯矩工况时控制梁的应变和挠度校验系数服从95%置信区间的正态概率图。 从图2 和图3 可见,各交点的变化大致在同一直线上,说明校验系数与其概率基本呈线性关系,认为箱梁应变和挠度校验系数服从正态分布(图中百分比表示相应校验系数占总体样本的百分比)。
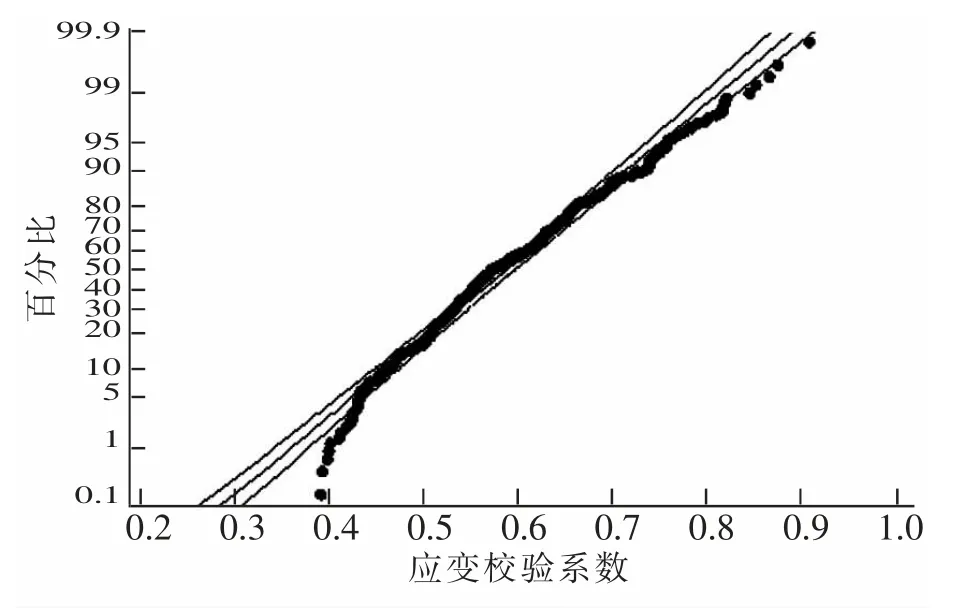
图2 最大正弯矩工况应变校验系数概率图Fig.2 Probability diagram of stress testing coefficient under maximum positive bending moment condition
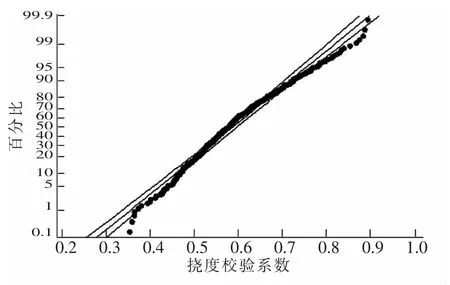
图3 最大正弯矩工况挠度校验系数概率图Fig.3 Probability diagram of deflection testing coefficient under maximum positive bending moment condition
按样本分类进行总体参数估计,校验系数常值范围按95%概率统计,对于服从正态分布的随机变量分布在区间[μ-2σ,μ+2σ]内的概率约有95%,再按精度0.05 取该区间的上限和下限作为校验系数常值范围。统计分析结果分别见表3 和图4~图7(图中频率表示相应校验系数分布概率)。
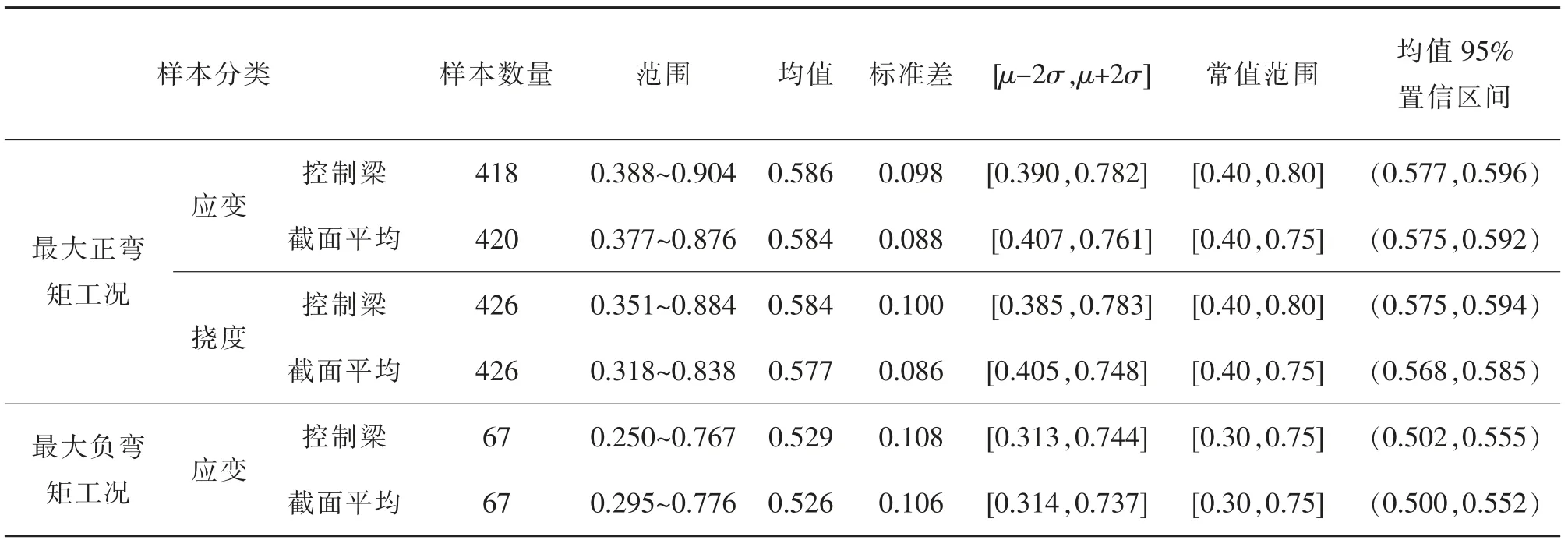
表3 校验系数统计分析表Tab.3 Statistical analysis of testing coefficient
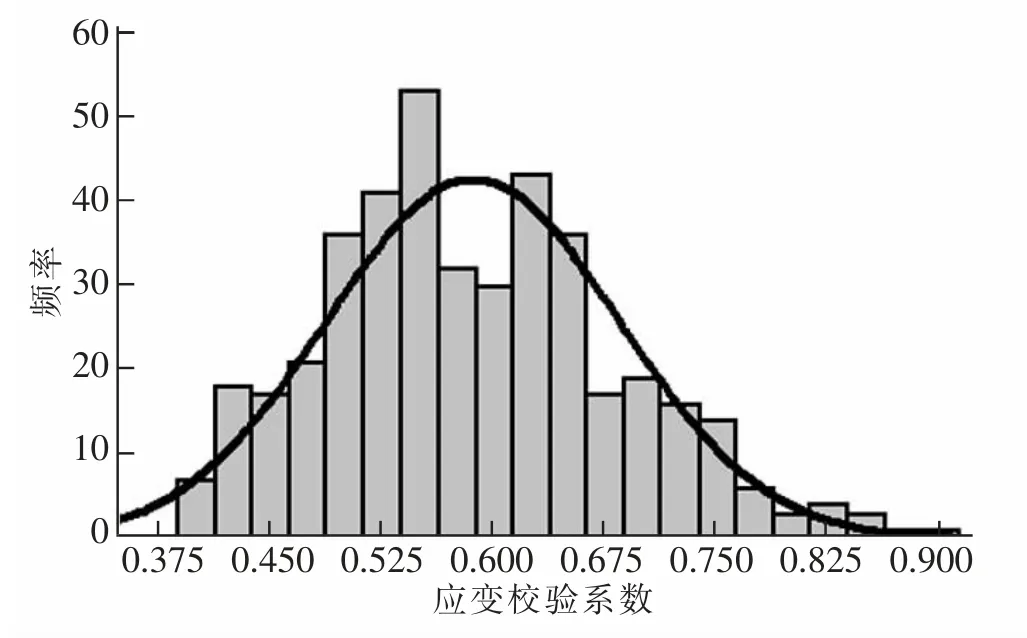
图4 最大正弯矩工况控制梁应变校验系数直方图Fig.4 Column diagram of stress testing coefficient under maximum positive bending moment condition
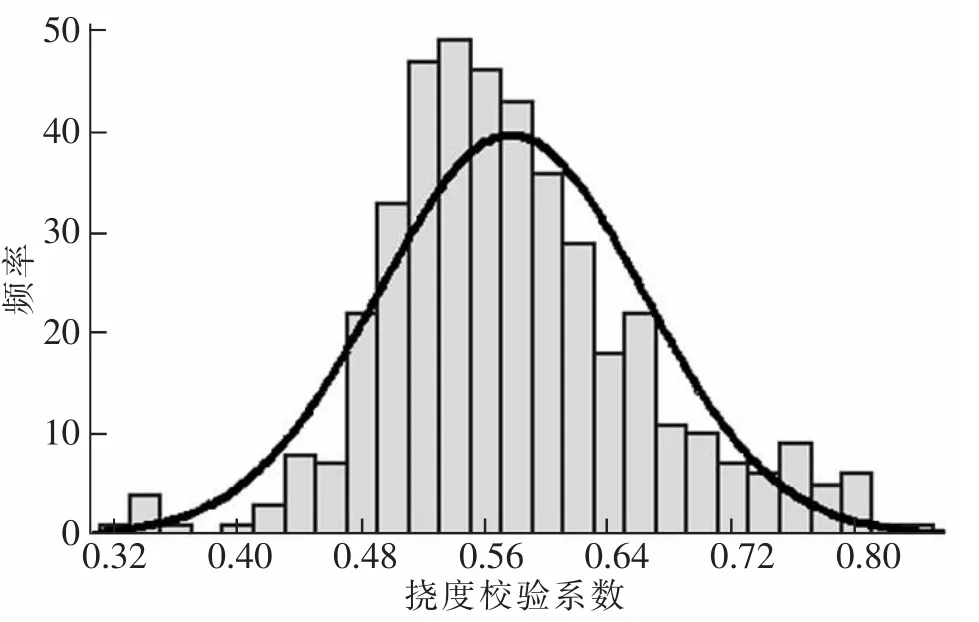
图5 最大正弯矩工况控制梁挠度校验系数直方图Fig.5 Column diagram of deflection testing coefficient under maximum positive bending moment condition
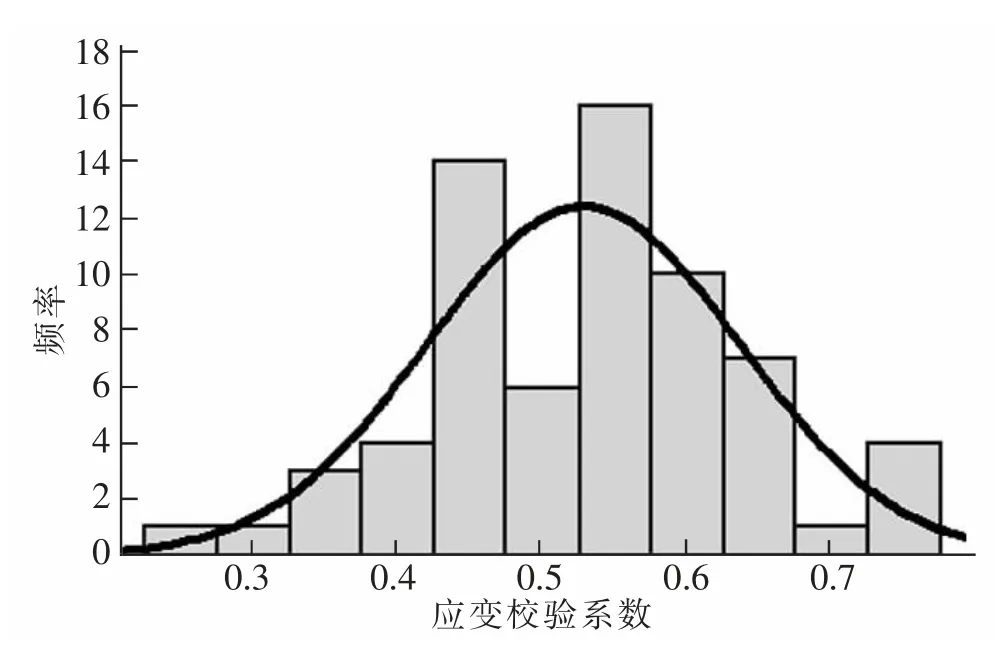
图6 最大负弯矩工况控制梁应变校验系数直方图Fig.6 Column diagram of stress testing coefficient under maximum negative bending moment condition
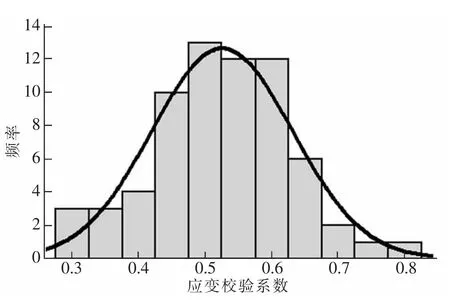
图7 最大负弯矩工况截面平均应变校验系数直方图Fig.7 Column diagram of average stress testing coefficient under maximum negative bending moment condition
通过以上分析可知,各类样本对应的总体标准差和均值置信区间均较小,说明试验数据离散度低,结果可靠。 在最大正弯矩工况时控制梁的应变和挠度校验系数常值范围均为[0.40,0.80],截面平均的应变和挠度常值范围均为[0.40,0.75]。 控制梁和截面平均校验系数常值范围很接近,截面平均的上限略小;因此可统一取[0.40,0.80]。 最大负弯矩工况时控制梁和截面平均的应变校验系数常值范围均为[0.30,0.75],与最大正弯矩工况时的[0.40,0.80]明显不同,表明按不同部位分别统计常值范围是合理的。本文校验系数常值范围分析结果与《荷载规程》差别较大,具体比较见表4。

表4 预应力钢筋混凝土小箱梁桥校验系数常值范围对比表Tab.4 Comparison of the testing coefficient of prestressed reinforced concrete small box girder bridge
3.3 正载和偏载校验系数分析
荷载试验工况加载根据横向位置不同分为正载(中载)和偏载两种方式,对多梁式桥正载的控制梁为中梁,偏载的控制梁为边梁。各组数据仍近似服从正态分布,正载和偏载下校验系数统计见表5。由分析结果可见,不仅应变在正偏载时、挠度在正偏载时的校验系数的统计结果接近,而且应变和挠度两者结果也很接近。校验系数是实测值和理论值的比值,当仅改变横向加载位置,其它影响因素不变时,校验系数影响很小,表明桥梁变形(变位)沿横向分布趋势与实际基本相符。 这也是对校验系数总体分析时,应变和挠度校验系数采用控制梁样本与截面平均样本所得到的统计参数非常相近的原因。从统计分析的角度说明采用梁格法并考虑部分桥面铺装刚度的计算模型在模拟小箱梁桥结构的横向联系上是和实际情况相符的,表明这种建模方式的合理性。
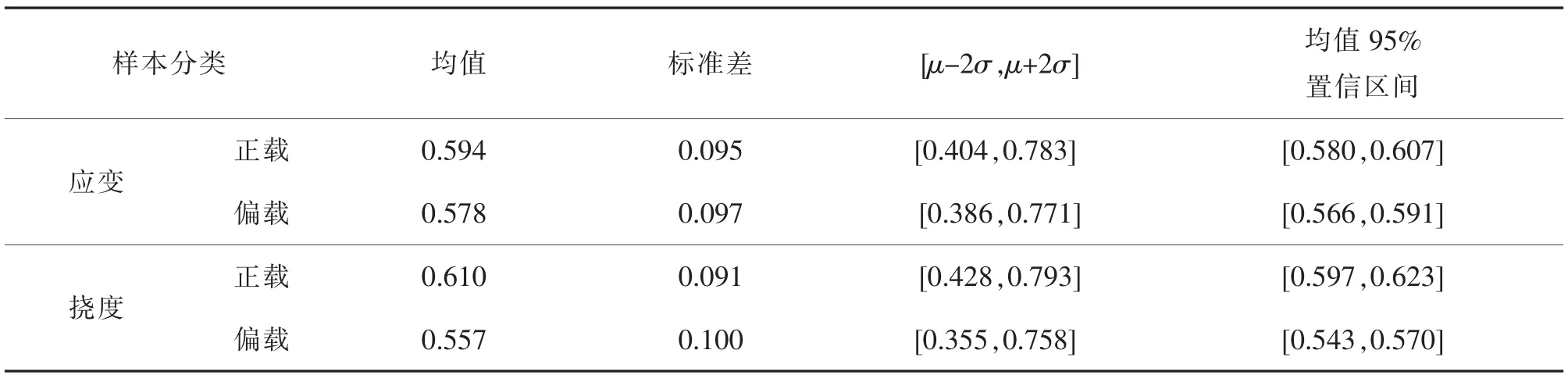
表5 正载和偏载下校验系数统计表Tab.5 Statistical table of testing coefficient under positive and partial load test
4 结论
1) 运用于新建桥梁的考虑校验系数常值范围荷载试验评定法, 精细化了传统荷载试验评定中校验系数的取值范围,取值范围更具有代表性。
2) 以考虑主要影响因素为限定条件选取样本, 最大正弯矩工况控制梁片应变和挠度异常值分别占样本总体的1.18%和0.07%,舍弃后的试验数据离散度减小。
3) 最大负弯矩工况与最大正弯矩工况应变校验系数常值范围分别为[0.30,0.75]和[0.40,0.80],按结构部位对常值范围进行分类,可明显提高校验系数常值的准确性。

