VW-MSPC 方法在变压器状态评估中的应用研究
王 勋,王豫新,康 琛,万 华,程宏波
(1. 华东交通大学电气与自动化工程学院,江西 南昌330013;2. 国网江西省电力公司电力科学研究院,江西 南昌330096)
以变压器运行状态为依据的变压器在线状态检修是现阶段变压器检修的发展趋势[1]。 现行的变压器状态评估标准[2]采用单变量的阈值比较法,判断方法简单、易行。但变压器发生故障时,各状态量变化并不是孤立的,针对单一变量逐个评估的单变量的阈值比较法对于变压器状态数据信息的利用并不充分,评估结果很容易出现偏差。针对这一问题,程宏波等[4]提出多元统计控制方法对变压器进行评估;吴奕等[5]提出基于熵权模糊物元和主元分析的变压器状态评价方法;张珂斐等[6]提出基于全维度的电力变压器智能决策支持系统研究,此外,人工智能算法[7]、图像识别[8]也被引入变压器状态评估中。
与其他评估方法相比,多元统计过程控制[9-10]判别过程利用数据的分布特性,不需要准确的数学模型,构造简单,实时性、可视化性能优异。 然而,基于马氏距离的传统多元统计过程控制无法反映变压器各指标变量重要性差异,在应用上受到一定限制。为此,在传统的多元统计过程控制方法的基础上引入加权马氏距离, 构建一种基于变量加权的多元统计过程控制 (multivariate statistical process control based on variable weighting, VW-MSPC),该方法在考虑变压器指标变量相关性的同时,兼顾反映了指标变量的重要性差异,可以客观、灵敏地反映变压器运行状态,为变压器状态检修提供参考依据。
1 变压器关键指标变量体系及变量的权重计算
1.1 变压器状态指标变量及各故障类型
变压器的状态指标变量可以有效的反映变压器的状态,正常情况下,变压器状态变量参数会在一定范围上下波动,对于变压器各状态指标变量测定、记录、评估是判断变压器运行过程是否发生异常的有效手段。
常见的9 种变压器故障类型为:F1 绕组故障,F2 铁心故障,F3 电流回路过热,F4 绝缘受潮,F5 电弧放电,F6 绝缘老化,F7 绝缘油劣化,F8 局部放电,F9 油流放电。
根据相关标准[2-3]筛选出试验数据充分的26 种变压器状态指标变量:H2含量,CH4含量,C2H6含量,C2H4含量,C2H2含量,CO 相对产气速率,CO2相对产气速率,铁心接地电流,铁心绝缘电阻,绝缘电阻吸收比,极化指数,绕组直流电阻互差,绕组电容量初值差,绕组绝缘介损,绕组短路阻抗初值差,绝缘油介损,油中含水量,油击穿电压,体积电阻率,油中含气量,局部放电量,油界面张力,糠醛含量,纸板聚合度,油流带电,顶层油温。
1.2 变压器各故障类型的关键指标变量提取及权重计算
对于不同的变压器故障类型需要合适状态指标变量进行评估,提取变压器各故障类型的关键指标变量能有效降低数据维度,去除冗余变量,提高变压器评估的准确性。
在无主观性需求的情况下,为保证评估方法的客观性,选用关联规则方法[11]筛选各故障的关键指标变量,并给出各故障指标变量的权重,使数据降维,权重给定,状态评估方法全部依赖于客观数据与客观的应用数学统计分析方法。 基于关联规则的关键指标变量筛选步骤如下:
1) 建立变压器关联规则的相关数据集
总集合D,包含所有的故障信息的事务数据库;子集A,故障发生后,某项超出警示值的指标参量的集合;子集B,发生某类故障的集合。
2) 计算变压器各故障类型与指标变量的支持度,置信度
定义Bf为出现第f 类故障事件,Ad表示第d 个指标变量超出注意阈值的事件,关联规则Ad→Bf的支持度S(Ad→Ff)与置信度C(Ad→Ff)可表示为
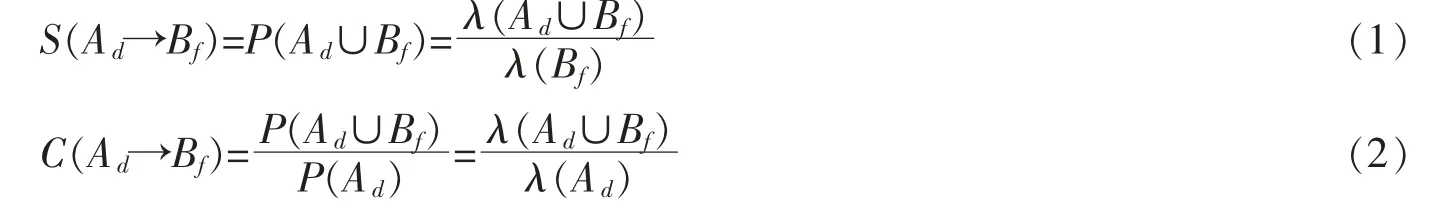
式中:λ(Bf)表示发生第f 类故障的总次数;λ(Ad)表示第d 个指标变量超出注意阈值的总次数;λ(Ad∪Bf)第f 类故障发生同时第d 个指标变量超出注意阈值的次数。
支持度和置信度是关联规则的两个基本的衡量度,支持度反映此关联规则的有效性,支持度越高,关联程度也越高;置信度反映此关联规则的确定性,置信度越高,该关联规则越可靠。
3) 根据支持度数据依次筛选出变压器关键指标变量。 支持度需满足条件

式中:min(S)为最小支持度阈值,相关文献表明,最小支持度阈值取70%就可以说明事件之间具有较高的关联性[12]。
4) 计算与变压器各故障相关的关键指标变量的权重
以关联规则中的置信度为标准计算的常权重系数作为变压器各故障关键指标变量的权重,常权重系数完全依赖于变压器失控状态,可以排除权重给定过程中主观性的影响。 权重计算公式为

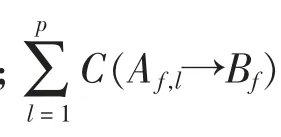
2 基于变量加权的多元统计过程控制
多元统计过程控制通过分析大量变量间具有相关性的过程数据和变量数据,利用假设检验的原理构造合适的多元控制图,通过多元控制图可以直观的判断系统运行状态。根据统计量计算方法不同,常用的多元控制图有多元T2控制图、多元累积和(multivariate cumulative sum,MCUSUM)控制图以及多元指数加权滑动平均(multivariate exponentially weighted moving average,MEWMA)控制图。 在三种控制图中,MEWMA 控制图每一个观测点都包含了历史信息的影响,针对不同的情况可采用不同平滑系数,具有反映过程变化的趋势、灵活性高等优点,适用于变压器运行状态评估。
2.1 MEWMA 控制图
对于MEWMA 控制图[13]介绍如下:
假设X 为相互独立的p 维随机变量X~N(μ0,ΣX),观测点总数为c。X 可排列为一个p×c 的矩阵,矩阵X的第i 列表示第i 个观测点样本值;矩阵X 第l 行Xl表示为第l 个指标变量。
对样本进行EWMA 滤波后第i 个样本变为Zi

式中:r 为平滑系数权重,r∈(0,1),当r=1 时,Zi退化为Xi;初值Z0取样本总体均值向量μ0。
对于第i 个观测点MEWMA 图的检验统计量定义为

式中:

式中:ΣX为受控状态下初始样本X 遵循的总体协方差;ΣZ表示样本EWMA 滤波后样本Z 遵循总体协方差。
为使组内波动小而组间差异大,提高控制图的抗异常干扰的能力,常对样本进行合理子组划分,即将相邻的n 个数据取均值作为样本来计算统计量。 检验统计量由(6)更改为

2.2 VW-MSPC 图
变压器不同的指标变量含有信息的重要程度是不同的,而MEWMA 图通过检验统计量对系统运行状态进行评估,其检验统计量式(8)实质上是一个马氏距离公式,该式虽然考虑了各变量之间的相关性与变量时序变化等因素,但并未涉及属性指标间的重要性差异对评估结果的影响,这对于变压器状态评估而言是不够的。 加权马氏距离是马氏距离公式的一种改进,在消除量纲,反映变量相关性的同时,还考虑了变量重要性差异的影响,在TOPSIS 方法[14],图像处理[15],聚类分析[16]的相关算法中加权马氏距离表现出了良好的去噪能力,因此考虑在MEWMA 控制图中引入加权马氏距离公式构造一种同时考虑指标变量重要程度与相关性的基于变量加权的多元统计过程控制(VW-MSPC)图,其检验统计量计算过程如下:
由于主观性和客观性因素,系统对于各指标变量有不同的敏感度,可分别用权重表示为矩阵形式

矩阵ω 中的每一个元素都与欲控制的指标变量一一对应, 为了使计算的检验统计量不产生较大的变化,各个指标权重之和满足

将加权马氏距离引入式(8)中得到VW-MSPC 检验统计量的计算式

式中:Ω 为权重矩阵中各元素的开方对角化矩阵。 当各变量权重值ωl都为1 时,式(11)退化成式(8),VWMSPC 图退化为MEWMA 控制图。
2.3 VW-MSPC 的控制阈值计算
若根据式(11)计算的检验统计量Qi值超过控制图的上限阈值UCL,表明系统在该点处于异常状态。 一般而言,决定多元控制图阈值的显著水平α 由3σ 原则确定,但这仅是一种经验方法,考虑到变压器运行状态检测的实际情况, 可根据各状态指标变量的标准差σ 和注意阈值μα来计算多元显著水平α 从而确定变压器各故障的上限阈值UCL。 其计算过程如下:
1) 计算各指标状态变量的一元显著水平αl。 由于变压器状态指标变量往往只有一个上限或下限注意阈值,同时各变量都为正值,所以一元显著水平αl计算公式为

式中:μol,μαl分别为第l 个状态指标变量的均值与注意阈值;normcdf 为正态分布累计概率密度函数;σl为各状态指标变量的标准差。
2) 计算变压器各故障评估对应的多元显著水平α。 计算各指标状态量的不同权重ωl,多元显著水平α可由以下公式计算

3) 确定VW-MSPC 图的阈值。 VW-MSPC 图的阈值确定方法与MEWMA 控制图相似,都是根据显著水平α,数据维度p,由ARL(average running length)曲线确定[17]。
3 实例分析
以江西某地一台220 kV 变压器发生电流回路过热(F3)故障为例说明VW-MSPC 方法的可行性。
3.1 关键指标变量体系的建立
根据2013—2017 年中国电科院设备状态统计数据整理出1 328 组与被测变压器型号相同、 运行环境近似、已知故障类型的变压器数据。 经统计,1 328 次故障中,发生电流回路过热(F3)故障次数λ(Bf)为131 次。表5λ(Ad∪Bf)=0 的指标变量未在表中显示)统计了F3 故障发生时所有指标状态量超过各自注意阈值的次数λ(Ad∪Bf),所有样本指标变量超过注意阈值的总次数λ(Ad)以及根据式(1),式(2)计算的各指标关于F3 故障的支持度与置信度。 同时统计变压器正常运行时,F3 故障时相关指标变量的均值μ0, 标准差σ,注意阈值μα,并根据式(13)计算各指标变量的一元显著水平αl,一同计入表1 中。

表1 F3 故障相关指标变量信息Tab.1 F3 fault related indicator variable information
规定min(S)为70%,根据支持度信息采用式(3)即可筛选出关键指标变量。例如C2H6含量对于F3 故障的支持度为λ(Ad∪Bf)/λ(Bf)×100%=37/131×100%=28.24%,小于70%,不是F3 的关键指标变量;而C2H4含量对于F3 故障的支持度为84.97%,大于70%,可作为F3 故障的关键指标变量。
最终筛选出的F3 故障的关键指标变量为:C2H4含量x1,CO 相对产气速率x2,CO2相对产气速率x3,绕组直流电阻互差x4,顶层油温x5。 根据式(4)可计算出各变量对应的权重矩阵为ω=[0.574,0.534,1.318,1.375,1.199]。
3.2 VW-MSPC 图的构建
根据表5 中一元显著水平αl信息采用式(14)可计算出F3 故障的多元显著水平=0.003 4,参考标准[2]中对于状态分数的划分比例,分别按60%,80%,100%显著水平将控制域划分为正常、注意、异常、严重4 个区域,通过对应的ARL 曲线求得该故障多元统计过程控制中正常到注意状态的阈值为16.642,注意到异常状态的阈值为17.280,异常到严重状态的阈值为17.637。
选取变压器该次故障之前包含F3 故障的5 个关键指标变量的300 组数据,使用Johnson 变换法将对应数据进行转换,使统计的数据接近多元正态样本,设定每组内个案数n=10,子组样本个数为30,平滑系数r=0.2,根据式(5)将样本进行EWMA 滤波处理后的样本数据和变量权重带入式(11)中计算该故障的VWMSPC 检测统计量。 子组样本数据以及检验统计量Q 如表2 所示。

表2 子组样本均值及检验统计量Tab.2 Mean and test statistics of subgroup samples
根据表2 中检验统计量数据可以绘制出F3 故障的VW-MSPC 图如图1(a)所示,对控制域区间进行等距处理,获得处理后的VW-MSPC 图如图1(b)所示。 通过图1 可以直观地判断出变压器关于F3故障的状态。
为得到变压器整体运行状态,按照上述计算过程,获得F1~F9 故障的检验统计量,将变压器各故障的检验统计量按显著水平的比例转化成百分制,其中检验统计量为0 时得分为100,达到异常阈值时得分为85,达到注意阈值时得分为75,达到严重阈值时得分为60,根据故障出现频次,对各故障对于变压器整体故障的权重比例矩阵为[0.120, 0.110, 0.111, 0.097, 0.114, 0.145, 0.101, 0.097, 0.105]。 当变压器各类故障均处在正常状态时,变压器整体评价按各故障的权重比例进行叠加;当变压器各类故障有一个除以异常及以上状态时,变压器的整体得分和状态评价参照最恶劣一类故障,由此可得到变压器整体状态VW-MSPC 图如图2(a)所示。 按照标准[3]的变压器评估方法获得变压器整体得分如图2(b)所示。

图1 电流回路过热VW-MSPC 图Fig.1 VW-MSPC diagram of current circuit overheating

图2 变压器整体状态评估Fig.2 Assessment of transformer integral state
在图2(a),图2(b)中,变压器处于正常运行时,电流回路过热的多元统计控制图曲线和国网标准的得分曲线都在正常区域上下波动,符合变压器运行的实际情况。 而图2(a) VW-MSPC 图显示变压器在第23个样本点进入异常状态,在第27 个样本点处变压器处于严重状态;图2(b)国家电网标准下的评估方法在第25 个样本点、 第30 个样本点处发现设备处于异常运行状态和严重运行状态, 检出时间均落后于VWMSPC 方法,这说明VW-MSPC 方法对变压器异常及以上状态具有更高的灵敏性。
3.3 故障样本的回顾检测
为进一步说明VW-MSPC 方法的检出效果,筛选2017—2018 年与被测变压器型号相同、运行环境近似的314 次变压器故障时的运行状态数据,选取每次故障之前的300 个数据点,分别使用标准[3]、MEWMA 控制图[4]、VW-MSPC 图进行回顾检测,故障检出率如表3 所示。

表3 回顾检测的故障检出率Tab.3 Failure detection rate of retrospective detection
表3 数据显示相对于国网标准、 传统的多元统计过程控制,VW-MSPC 方法对于变压器的各类故障都有较高的故障检出率。
4 结论
1) 在传统的多元统计过程控制中引入加权马氏距离, 提出一种基于变量加权的统计过程控制方法对变压器运行状态进行评估,同时考虑了变压器变量之间的相关性以及指标变量重要程度差异信息,克服了传统多元统计过程控制中计算最终统计量时各变量权重一致的问题,在充分利用变压器运行状态数据的基础上,得到一种构造简单、实时性、可视化性能优异的变压器状态评估方法。
2) 关联规则方法使用变压器历史运行过程中的故障信息, 计算变压器各故障类型与各状态指标变量数据的支持度、置信度。 利用支持度信息筛选出各故障的关键指标变量,可以有效地减少数据维度,提高变压器状态评估的准确性,利用可信度信息提供各故障类型关键指标变量权重,使权重的给定完全依赖于失控状态,排除权重给定过程中主观性的影响。
3) 电流回路过热故障的实例分析表明VW-MSPC 方法可以根据变压器运行状态数据很好地评估变压器运行状态,相较于现行变压器检测标准,该方法对变压器异常及以上状态具有更高的灵敏性,能够更快地检测出变压器异常;通过对历史故障数据的回顾检验表明VW-MSPC 方法对于变压器运行故障的检出的准确率较高。

