CATIA曲面法向量和坐标转换的算法研究与应用
张继承
(航空工业洪都公司,江西南昌330024)
长期以来,CMM(Coordinate Measuring Machine)数据源大多通过UG三维CAD/CAM软件进行采集,针对CATIA数模也是先通过软件转换接口将其转换为UG数模,然后再通过UG三维CAD/CAM软件进行数据源采集。这主要是因为UG软件具有点的几何属性输出功能(曲面上点的坐标及在该点的法向量等信息),而CATIA软件没有该功能。但随着时代的发展,CATIA软件相对于UG软件所具有的优势愈发突出,如曲面造型功能,使得CATIA软件在制造业中越来越普及。企业为了解决CATIA数模CMM数据源的问题,通常采取以下两种措施:一是自行或委托第三方对CATIA软件进行二次开发;二是通过市场采购第三方成熟软件。
针对上述情况,本文开展了曲面法向量和点坐标转换的算法研究,并根据曲面法线方程及方向余弦的表达方法提出了一种曲面上任意一点法向量的数学建模方法;通过使用CATIA软件针对VB平台提供的专用函数,获取曲面上目标点坐标并对目标点单位法向量进行方向修正;再根据坐标变换原理将目标点及法矢量从模型坐标系转换到测量坐标系,最后对开发的软件进行应用验证。
1 曲面法向量
1.1 曲面法线方程及方向余弦
曲面法线示意图如图1所示。
已知曲面Σ的方程

则可求得该曲面 Σ在点 M(x′,y′,z′)处的法线方程[1]
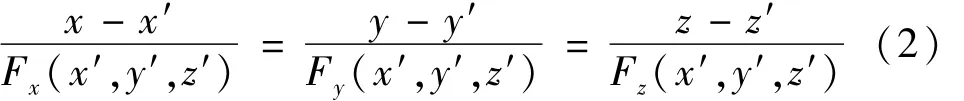
设α,β,γ分别为曲面Σ在M点的法线与X,Y,Z轴的夹角,令 fx=Fx(x′,y′,z′),fy=Fy(x′,y′,z′),fz=Fz(x′,y′,z′),则曲面 Σ在点 M的法线方向余弦可表示为[1]
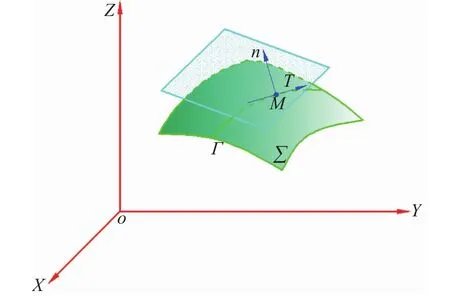
图1 曲面法线示意图
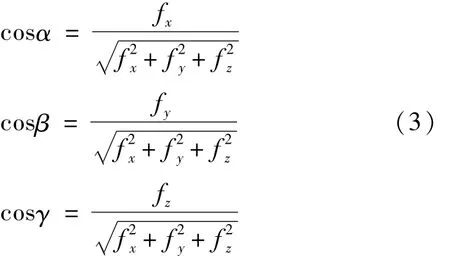
1.2 曲面法向量表示
由上文可知曲面 Σ在点 M(x′,y′,z′)的一个法向量可表示为[2]
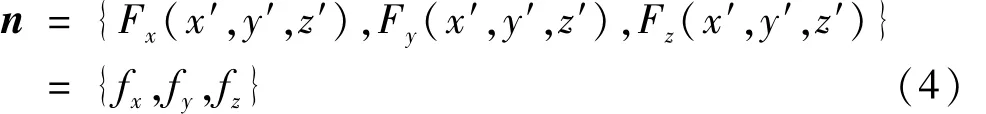
若能知道该曲面的方程和点M的坐标则可计算出其法向量n,但是就CATIA软件而言,只有法国达索公司才能得知其曲面构造函数。
1.3 曲面法向量的数学建模及求法
由于上述方法不能用于CATIA二次开发,本文将建立一种全新的数学模型(如图2所示)求解曲面法向量n。
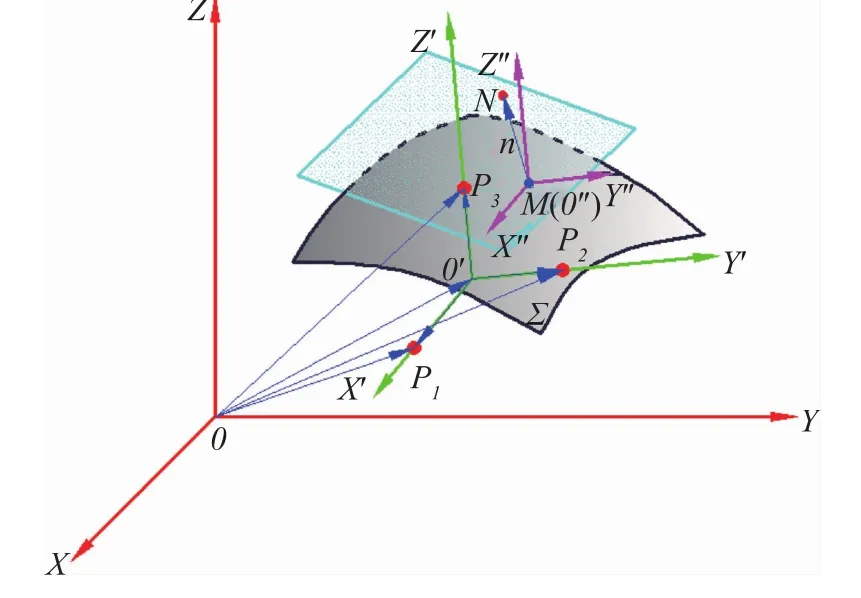
图2 曲面法向量数学模型
设模型中存在一个原始坐标系O-XYZ、一个新坐标系O′-X′Y′Z′和一个曲面 Σ,其中新坐标系原点 O′在原始坐标系中的坐标为(x0,y0,z0),点M为曲面Σ上一点,向量为曲面Σ在点M处的单位法法向量。在坐标轴 X′,Y′,Z′上依次取 3个点 P1,P2,P3,这三个点在新坐标系中的坐标分别为(1,0,0),(0,1,0),(0,0,1),即向量分别为平面 Y′O′Z′,X′O′Z′,X′O′Y′的单位法向量。设点 P1,P2,P3在原始坐标系中的坐标分别为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),则
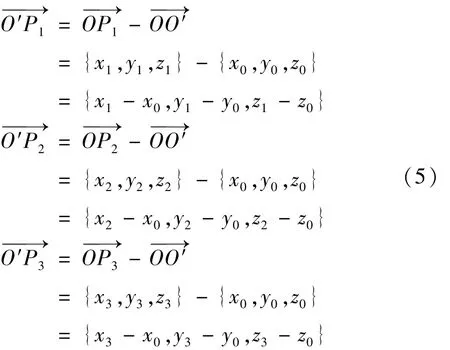
式中:x1-x0,y1-y0,z1-z0分别为向量Y,Z轴上的分量;x2-x0,y2-y0,z2-z0分别为向量轴上的分量;x2-x0,y2-y0,z2-z0分别为向量在 X,Y,Z轴上的分量。
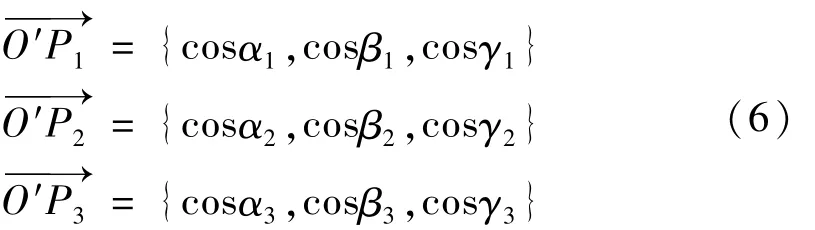
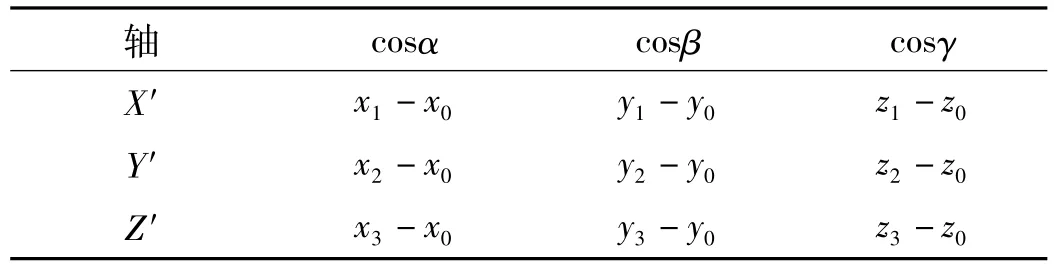
表1 X′,Y′,Z′轴在O-XYZ的方向余弦(公式法)
过点M建立一个新坐标系O″-X″Y″Z″,坐标系原点 O″与点 M重合,坐标系 O″-X″Y″Z″与坐标系 O′-X′Y′Z′互为平行关系,即相当于坐标系 O′-X′Y′Z′从点O′处平移到了点M处,因此坐标轴X″,Y″,Z″在坐标系O-XYZ的方向余弦值与坐标轴X′,Y′,Z′在坐标系O-XYZ的方向余弦值相同。设单位法向量在坐标轴 X″,Y″,Z″的分量分别为 i,j,k,现用 n表示曲面Σ在点M处的单位法向量,则有

关于i,j,k的具体求解方法法大致有两种思路(具体详见本文1.6部分):
1)用点 N在坐标系 O′-X′Y′Z′中的坐标值减去点M在坐标系 O′-X′Y′Z′中的对应坐标值。设点N,M在坐标系 O′-X′Y′Z′中的坐标分别为(i′,j′,k′),(x′,y′,z′),则有
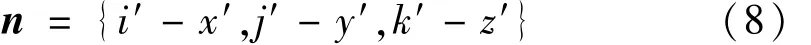
2)获取点N在坐标系O-XYZ中的坐标,然后利用本文所提供的线性关系式计算出点N在坐标系O″-X″Y″Z″中的新坐标即可。
1.4 曲面法向量的方向修正
CATIA软件针对VB平台提供了“GetDirection”,“GetMeasurable”,“GetWorkbench”等几个重要函数,通过这些函数可间接求得曲面的单位法向量,其中函数“GetWorkbench”用于获取SPAWorkbench对象(空间分析),函数“GetMeasurable”用于通过 SPAWorkbench对象获取Measurable对象(测量),函数“GetDirection”用于通过Measurable对象获取直线的反方向[3]。通过此法可求得图2中法线O″N的反方向n′={dr(0),dr(1),dr(2)},进而可求得其在世界坐标系下的单位法向量。
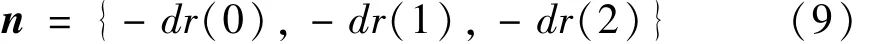
1.5 点的坐标转换
由于CATIA针对VB提供的提取点位函数“GetCoordinates”,“GetPoint”只能导出世界坐标系下的坐标值,而获取工作坐标系下的坐标值则需要通过坐标转换算法实现。目前关于点的坐标转换有很多种方法,如方向余弦法、欧拉角法(共12种旋转顺序)、欧拉轴角法、四元数法等[4],大体上可分为主动法和被动法两类。
1.5.1 主动法
主动法是让空间点M围绕原坐标系进行一系列的平移、旋转的转换算法(从点M在坐标系O-XYZ上的位置M1变换到点 M在坐标系 O′-X′Y′Z′上的位置 M2),而原坐标系不发生任何变化(实质上相当于让原坐标系O-XYZ充当了新坐标系 O′-X′Y′Z′)。具体在 CATIA中可通过定位变换法手动实现,VB语言则可通过HybridShapeFactory类的AddNewAxisToAxis方法来自动实现,其基本原理是让工作坐标系与世界坐标系重合,数模从工作坐标系位置转换到世界坐标系位置,此时世界坐标系下的坐标值与工作坐标系下的坐标值重合。
1.5.2 被动法
被动法是通过一定的平移、旋转让原坐标系OXYZ与新坐标系O′-X′Y′Z′重合的转换算法,而点M不发生任何变化。常见的算法是先求出平移矩阵T和旋转矩阵R0,然后利用坐标变换公式计算出点坐标。
设有两个原点相同的直角坐标系O-XYZ与O′-X′Y′Z′,如图3所示,任意一点M在这两个坐标系中的坐标分别为(x,y,z),(x′,y′,z′)。
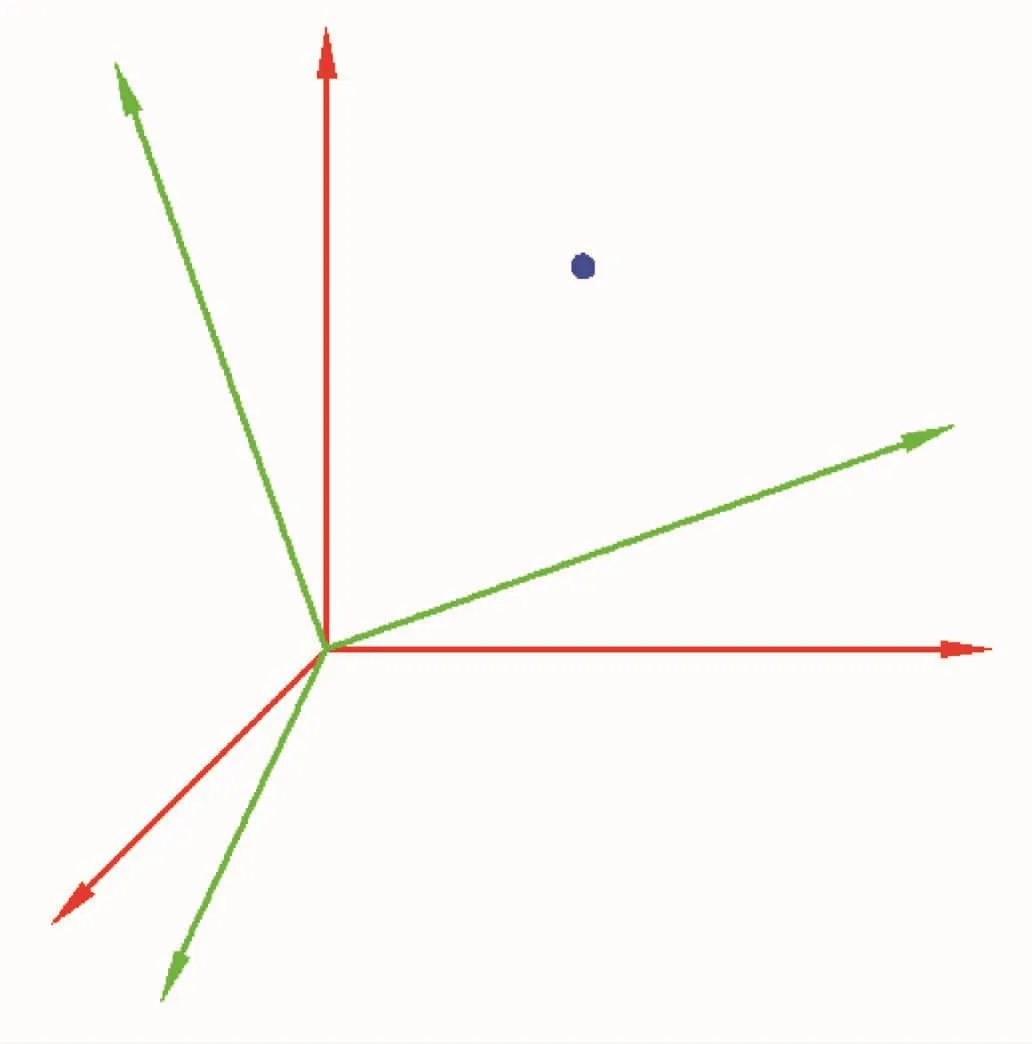
图3 两个原点相同的直角坐标系
设X′,Y′,Z′轴在 O-XYZ坐标系中的的方向余弦为表 2所示内容[5],则(x,y,z)与(x′,y′,z′)的关系可表示为[5]
1)线性关系式
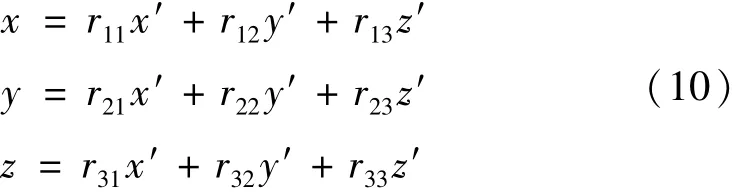
2)矩阵关系式
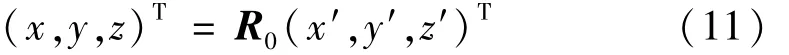
式中:R0=(rij),称为旋转矩阵。

表2 X′,Y′,Z′轴在O-XYZ的方向余弦(系数法)
如果原点O′在O-XYZ坐标系的坐标为(x0,y0,z0),则有
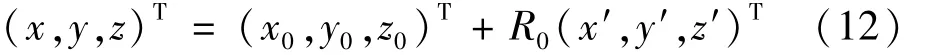
则(x′,y′,z′)与(x,y,z)的关系可表示为[5]
1)矩阵关系式
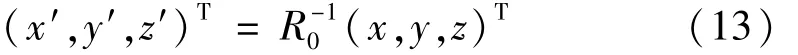
根据表2可知,X,Y,Z轴在 O′-X′Y′Z′的方向余弦如表 3[5]。

表3 X,Y,Z轴在 O′-X′Y′Z′的方向余弦(系数法)
2)线性关系式
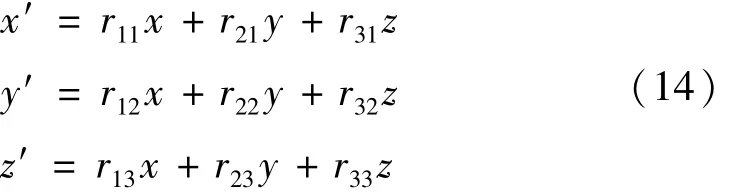
式(14)的系数矩阵是式(10)的系数矩阵的转置矩阵RT,结合式(11),可得出矩阵形式为
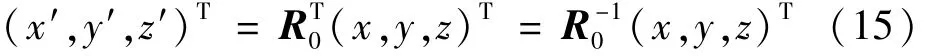
如果原点O′在O-XYZ坐标系的坐标为(x0,y0,z0),由于=E=I,则有
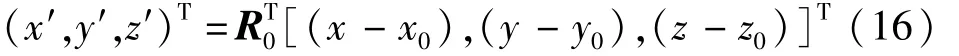
计算过程中必须首先获取坐标系O-XYZ与O′-X′Y′Z′的方向角,方法可分为二种:一种是通过手动测量得到各个角的度数;另一种是通过CATIA针对VB提供的函数“GetAngleBetween”测出角度。因后者测出的角度不能正确处理两线间的正向关系,有时测出的是π-α角,有时测出的是 α角,且 cos(π-α)=-cosα,所以根据传统算法进行计算可能会造成坐标计算错误,法线方向有可能被取反,与CMM测量型面所需的外法向要求不符,在实际测量中可能导致测头与工件发生碰撞。
根据1.3内容和上述推导,可得出表4内容及利用VB对CATIA进行二次开发求点坐标转换的算法关系式。

表4 X,Y,Z轴在 O′-X′Y′Z′的方向余弦值(公式法)
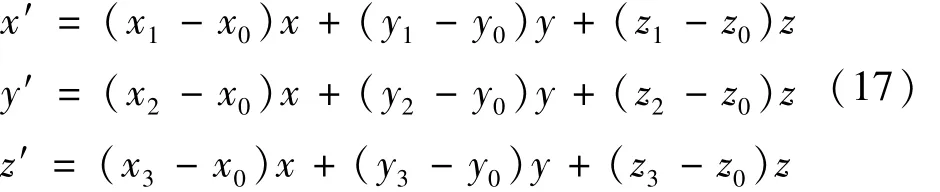
式中:(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)分别为图 2中点 P1,P2,P3的坐标,(x′,y′,z′),(x,y,z)分别为空间点 M在坐标系 O′-X′Y′Z′和 O-XYZ中的坐标。
如果原点O′在坐标系 O-XYZ中的坐标为(x0,y0,z0),则需对式(17)进行平移转换,因此可得
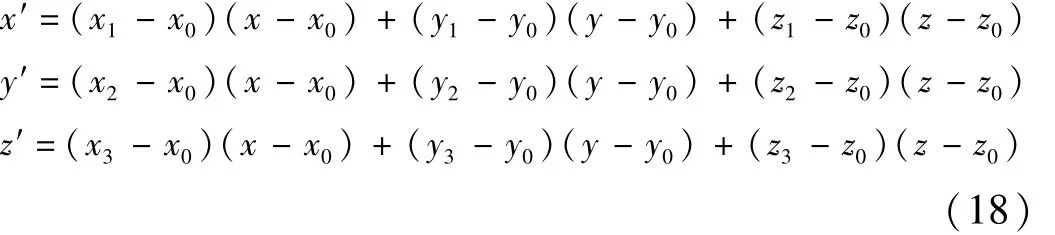
1.6 曲面法向量的实现
1.6.1 曲面点M和法向量点N坐标已知情况下
现设点N为曲面Σ在点M处的外单位法向量的顶点,点N,M在坐标系O-XYZ中的坐标分别为(nx,ny,nz),(x,y,z),如图 4所示,其中坐标系 O″-X″Y″Z″相当于坐标系 O′-X′Y′Z′从点 O′平移到了点 M,即坐标轴 X,Y,Z在坐标系 O′-X′Y′Z′,O″-X″Y″Z″的方向余弦值相同。原点O″与点M重合,其在坐标系O-XYZ中的坐标亦为(x,y,z)。因此,根据式(18)可知点 N在坐标系 O′-X′Y′Z′中的新坐标(i,j,k)为
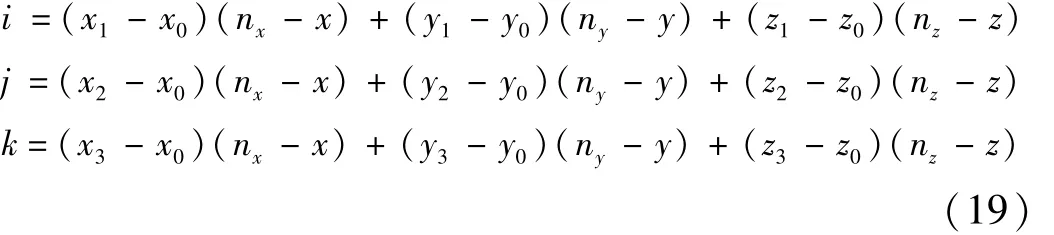
式中:(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)分别为图2中点P1,P2,P3在坐标系O-XYZ中的坐标,根据点 N在坐标系 O″-X″Y″Z″中的新坐标(i,j,k)可求出曲面Σ在点M处的外单位法向量{i,j,k}。
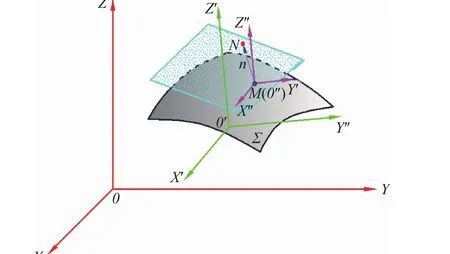
图4 曲面法向量转换示意图
1.6.2 曲面点M法线反方向数据已知情况下
根据1.4和1.6.1内容可知,式(9)中 nx-x=-dr(0),ny-y=-dr(1),nz-z=-dr(2)
故式(19)可转化为
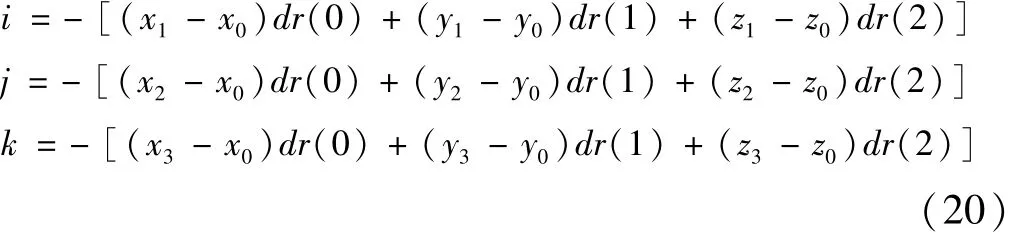
2 “CMM测量点采集辅助软件”开发
基于上述分析研究成果,开发了“CMM测量点采集辅助软件”,软件运行效果和数据输出效果均达到了预期的目标,下面具体进行介绍。
2.1 软件概况
“CMM测量点采集辅助软件”由导出、导入、点位、恢复模块四部分组成:导出模块主要用来提取测量数据;导入模块主要用来导入外来数据生成点云和验证导出数据的正确性;点位模块主要用来生成点位图供打印或抓图;恢复模块主要用来恢复点位模块使用前的CATIA窗口环境。因为生成点位图时CATIA窗口环境会发生变化,如背景色变为白色等,点位模块与恢复模块为互斥关系。软件设计流程见图5所示。
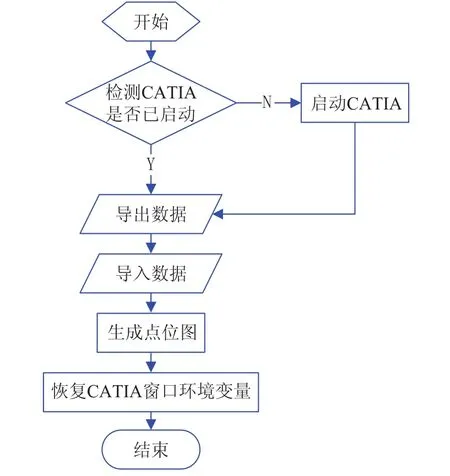
图5 软件组成
2.2 软件主要功能介绍
本软件最主要的功能是从CATIA给出的CAD模型中导出准备测量的数据。软件所提供的导出模块支持以毫米与英寸为测量单位的数据导出功能;测量点选取类型支持坐标点、线上点、面上点、交点、投影点、孔中心点、切点等类型;测量点选取方式支持粗选、手选、集选3种方式;测量型面选取方式支持手动选取和自动拓扑选取2种方式,测量型面选取时会自动生成参考法向量方向箭头,若遇特殊情况,箭头指示方向与预期相反时,只需将该测量型面上已导出的点的单位法矢数据乘以-1即可(或使用型面法矢反转功能)。数据导出过程中,可自动检测出体外点、非测量型面点、坐标系原点、重复点等错误点,并在信息页面列出有关错误的详细情况,具有一定的防错功能。数据导出精度可自选且数据按照“N,X,Y,Z,I,J,K”格式进行输出,以txt文件格式进行保存。考虑到使用的方便性,未对数据进行任何加密保护。导出模块程序设计流程如图6所示,其整体运行效果和数据输出结果见图7,8所示。
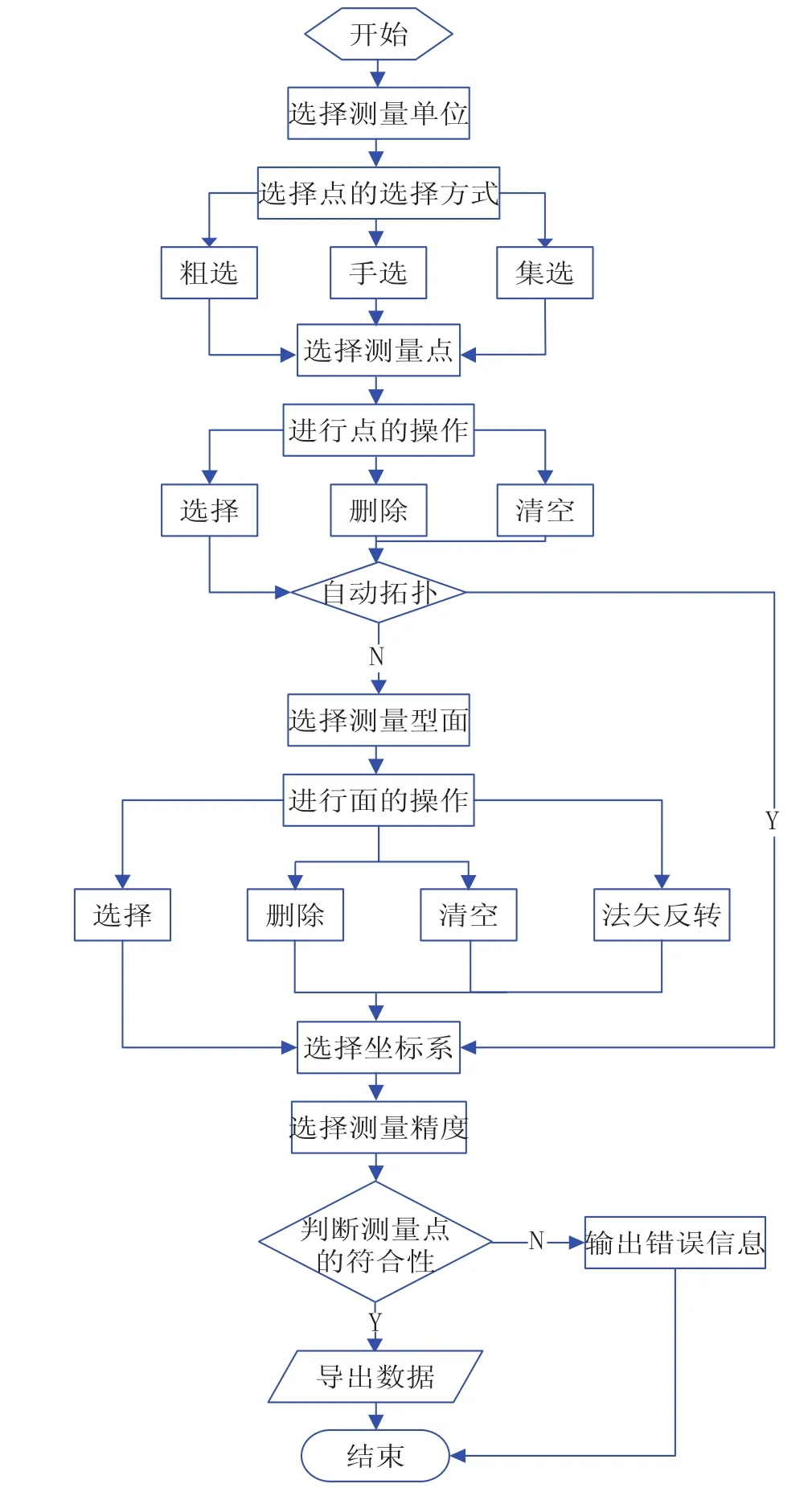
图6 数据导出模块程序设计流程图
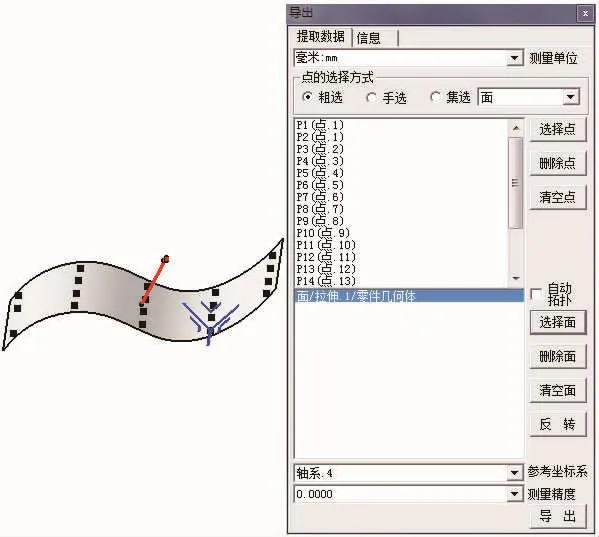
图7 软件运行过程界面
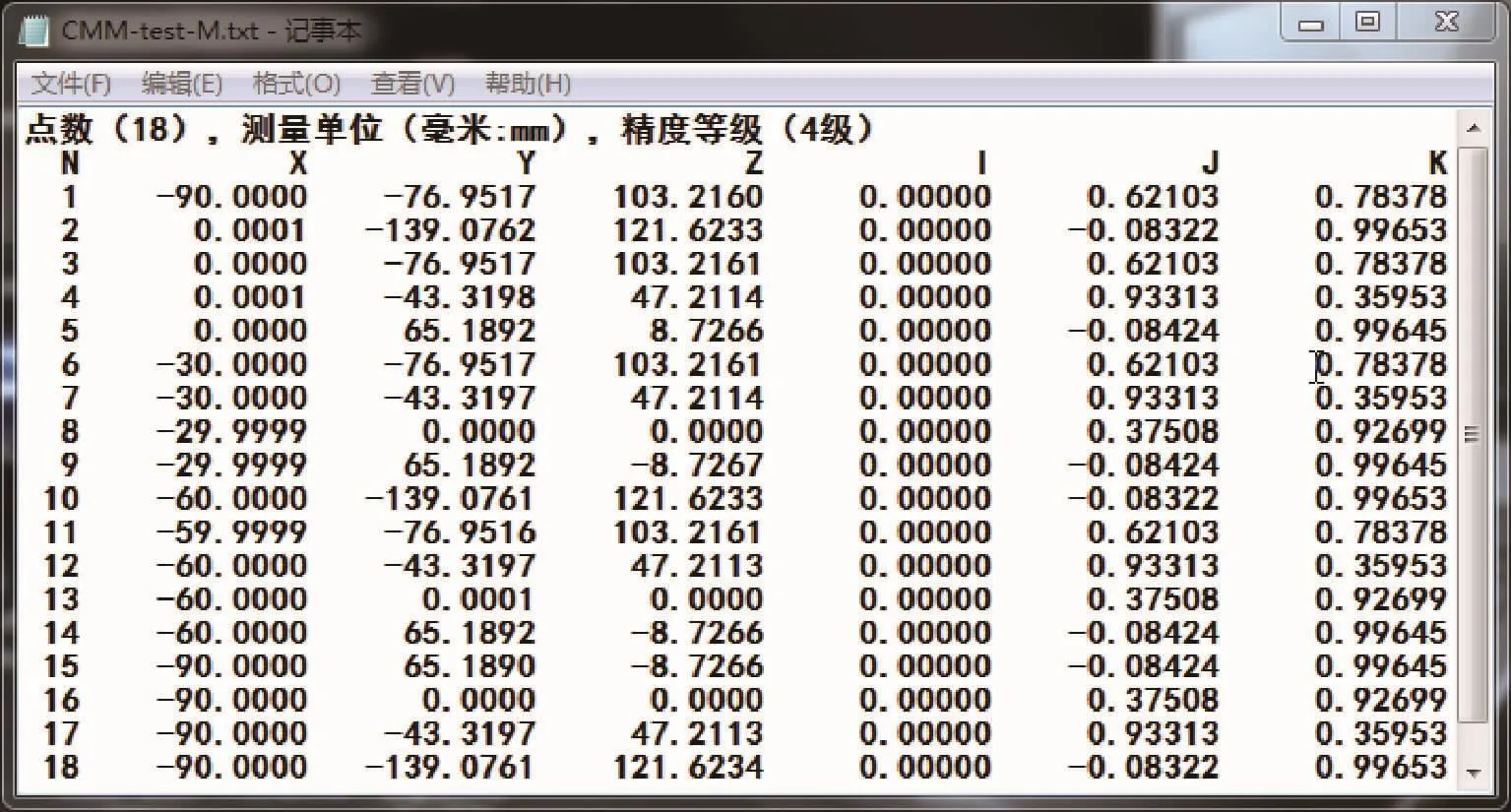
图8 测量数据输出效果
为了验证软件导出数据的正确性,在导入模块中增加了曲面点位法矢的导入验证功能,因此导入模块不仅具有导入外来数据功能,而且还具有验证导出模块所导出测量数据的点位及点位法矢的正确性功能,软件运行效果如图9所示。为了易于观察,软件将点位法矢的长度设为30,而不是传统的1,并用红色显示,若导入点未生成点位法矢,则意味着导入数据未提供单位法矢或所提供的单位法矢数据有误,需自行研判数据。
3 结束语
为解决CATIA数模的CMM数据源问题,提出了一种CATIA曲面法向量和坐标转换算法。基于该算法,利用VB语言成功开发出CMM测量点采集辅助软件,并已取得相关软件著作权。本文的研究为其它CAD/CAM软件进行类似功能的二次开发提供了参考,同时可为企业节约一定的软件开发、采购和维护成本。

