面向高速实时数据处理的无锁内存分配算法
李文浩,方景龙
(杭州电子科技大学计算机学院,浙江 杭州 310018)
0 引 言
高速实时系统应用中,内存管理起着十分关键的作用。由于程序运行阶段的内存分配皆由动态内存分配算法来完成,使得动态内存分配在内存管理上尤其重要。伙伴(Buddy)算法凭借其较高的分配效率与内存利用率,成为一种应用广泛的经典算法。但是,Buddy算法仍存在一系列不足,特别是在高并发环境下,算法效率有较大的下滑。目前,对Buddy算法的改进大都集中在延时合并以及外碎片方面,对并发性的改进研究较少。本文针对高速实时系统的高并发特点,在Buddy算法的基础上,提出一种无锁内存分配(Lock Free Memory Allocation, LFMA)算法,并通过渐进式重合并策略实现了延时合并及降低外碎率的效果。
1 Buddy算法
Buddy算法在动态内存分配相关文献中出现频率较高,Linux内核也使用该算法进行内存分配[1]。Buddy算法维护多个空闲队列,大小为2m个页的内存块都被链入同一个队列中,其中m的最大值为mmax。当要分配一个大小为b页(2i-1 单生产者多消费者是一种高速实时系统的常见模型。如在短波实时显控系统中,信号采集线程不断申请内存以存储从硬件采集的信号数据,根据数据类型分别交由解析线程池、绘图线程和存储线程进行处理,随后在这些线程中释放内存,这给内存分配算法带来同步问题。文献[10]对锁和原子操作的性能进行测试,结果显示原子操作的性能约为锁的2倍,同时Cache命中率也是关乎高速实时系统性能的一个重要问题,每当出现一次Cache miss都要花费数百个时钟周期到内存中重新读入数据到高速缓存。Buddy算法采用的链表结构无疑增加了Cache miss的机率。因此,LFMA采用原子操作做为同步方式,并用位图这一连续的数据结构降低了Cache miss的概率。 由于每一个页框只能是被分配和空闲两种情况,因而,可以使用位图标记每一个页框的状态,位图中每一位与一个页框相对应,若某页框被分配则对应位为0,若页框空闲则对应位为1,再将位图结合原子操作以达到无锁分配。LFMA算法包含一个一级位图,其中每一位对应当前一个页框的使用状态,其结构如图1所示。 图1 LFMA算法结构 类似于Buddy算法的空闲队列,LFMA维护了多个空闲表,每个空闲表由搜索位图和二级位图构成。其中二级位图用于标识空闲内存块,如,当存在2k大小的空闲内存块时,第k个空闲表的二级位图中对应该空闲内存块首页框的位被标记为1。为了加快找到第一个空闲块的速度,引入搜索位图,每一位对应二级位图中的一个位图切片(每张位图是一个整型数组,而其中的一个整型称之为位图切片),若位图切片为0,则搜索位图中对应位为0,否则为1。 在高并发程序中,临界区是影响性能的主要原因,当使用锁做为同步方式时,由于同一时刻只有一个线程可以处于临界区,因此,系统在临界区的消耗如下: (1) (2) Hlock=LAVG×T+OAVG×T (3) (4) Hatomic=AAVG×T+OAVG (5) 式中,Hlock为采用锁同步时系统在临界区的消耗。LAVG为加锁操作的平均消耗,假设共加锁n次,其中m次发生了Cache miss,第i次发生Cache miss时的加锁消耗为Lcm(i),未发生Cahce miss时的第i次加锁消耗为Lc(i),那么平均加锁消耗可由公式(1)计算得出,即总耗时除加锁次数n。OAVG为普通指令的平均消耗,假设临界区内共有n条普通指令,其中m条执行时发生了Cache miss,第i次发生Cache miss时的消耗为Ocm(i),未发生Cache miss的第i次操作消耗为Oc(i),那么普通指令的平均消耗可由式(2)得到。T为等待在临界区的线程数。当使用原子操作时,在该段临界区的消耗可由式(5)表述,其中Hatomic为采用原子操作时系统在临界区的消耗。AAVG为原子操作的平均消耗。若执行n次原子操作,其中m次发生了Cache miss,且第i次发生Cache miss时的消耗为Acm(i),未发生时为Ac(i),那么原子操作的平均消耗可由式(4)得出。对比式(3)和式(5)可以发现,采用原子操作时,由于临界区可以有多个线程同时进入,因此普通指令的执行可以并发执行,在公式上的体现便是OAVG无需乘以T。由于LFMA算法采用了连续的数据结构,从而降低了Cache miss概率,又由于原子操作的性能约为锁的2倍,因此LAVG>2AAVG。综上所述可知Hlock>Hatomic,即采用原子操作的消耗小于采用锁做为同步方式的消耗。 独个原子操作具有原子性,但多个原子操作却不一定是原子的。因此,虽然设置搜索位图和设置二级位图的操作都是原子的,但两者组合起来却不一定是并发安全的。比如,当出现表1所示的执行顺序时,会导致某个位图切片明明不为0,但搜索位图中的相应位却为0。 表1 造成多级位图出现竞态问题的一种执行顺序 这个问题可以通过加锁解决,但违背了LFMA算法的无锁原则,因此LFMA采用了双判法。即内存申请线程将搜索位图设置为0后再判断一次二级位图中对应切片是否为0,若不为0则重新将搜索位图中相应位置设为1。 在诸如短波实时显控这样的高速实时系统中,其申请内存块的生命期通常较短,导致Buddy算法不断分裂和合并内存块,文献[11]提出延迟合并的思想,但并未给出具体实现,本文针对这一问题,采用渐进式重合并策略。LFMA算法中,当释放内存后,并不立即进行内存块的合并,而是当某大小内存块数量不足时才进行渐进式重合并。其合并过程为一级位图的分步搜索过程,内存分配者通过位运算在位图中从前向后搜索连续1的个数,随后将这些空闲页合并为尽量大的内存块并设置相应的二级位图与搜索位图。每当合并出一个空闲块,LFMA算法都会检查本次合并所花费的时间是否超过重合并最大时间限制,若超过,则记录本次进行到一级位图的第几位,以便下一次合并操作继续执行。通过渐进式重合并,相较于Buddy算法,LFMA算法不仅减少了在频繁申请释放内存时因不断拆合内存块所带来的负载,还减少了外碎片。 为了验证LFMA算法的效率,首先进行模拟实验。模拟实验选用Buddy算法做为对照组,并添加了一个直接向操作系统申请内存的实验组做为参照组。实验在两种不同环境下进行,第一种是单线程申请释放内存,第二种是单个内存申请线程和多个内存释放线程,即单生产者多消费者模型。除模拟实验外,还测试了LFMA算法与Buddy算法在短波显控系统中的实际表现。 3.2.1 单线程下的分配效率 3个实验组在单线程下进行n次不断申请和释放内存,每次申请的大小为(0,4]MByte的随机值来模拟短波显控系统中采集数据的大小范围,所消耗的时间总和如图2、图3所示。 图2 LFMA与Buddy的内存分配时间 图3 向操作系统申请内存的时间 根据图2可知:在单线程下,LFMA的内存分配速度优于Buddy,分配效率提升约31%,这主要有2个原因,一是Buddy算法要不断进行伙伴块的拆分与合并,其中还涉及到链表的插删操作。二是Buddy维护的是一个链表队列,而链表不是连续的存储单元,因此读取缓存行时更容易出现Cache miss。对比图2和图3可以发现:首先向操作系统申请一块内存做为内存池,之后再在应用层调用内存分配算法进一步分配,其效率远远高于频繁的向操作系统申请和释放内存。主要是由于每次向操作系统申请和释放内存都需要进行虚拟地址到物理地址的映射操作,从而导致效率低下。 3.2.2 单生产者多消费者的分配效率 为了模拟高并发生产环境,实验使用一个线程做为生产者不断申请内存,之后通过一个队列传递给多个消费者线程,消费者线程进行内存的释放。实验统计了在不同消费者数量下,LFMA和Buddy完成一百万次内存分配和释放的时间,结果如图4所示。观察图4可以发现:随着消费者线程的增加,对锁的争抢更加频繁,导致Buddy算法效率不断下降,而LFMA采用的是无锁数据结构,因此随着线程数的增加其效率下降相对平缓,且效率高于Buddy,平均性能提升约27%。 图4 多线程下LFMA与Buddy的分配时间 3.2.3 在短波显控系统中的应用 在较为理论化的环境中进行模拟实验后,将LFMA算法与Buddy算法在实际生产环境中进行测试,分别测试两者运用于短波显控系统时系统的实际效率。在实际生产中,随着采集速率的变化,一般通过调节解析模块线程池的线程数来匹配采集速率,采集线程与解析线程池构成的单生成者多消费者模型是系统的关键瓶颈,为此,实验记录了在不同线程数量下系统解析模块的性能变化,具体如表2所示。 表2 不同内存分配算法与并发量下的数据解析速度 帧/s 观察表1可以发现:当解析线程池只有3个线程时,LFMA算法与Buddy算法对系统性能的影响并不大,因为此时主要瓶颈在于解析速度,线程间内存分配释放的并发度不高;随着线程数量的增加,内存释放的速率加快,对锁的争抢变得密集。由于LFMA算法采用的连续数据结构有着比Buddy算法更低的Cache miss率,所以,采用LFMA算法与Buddy算法的性能差异也随着并发度的提高逐渐体现出来;当线程数增加到30时,解析线程池的处理能力并没有一直增加,这是由于随着线程的不断增加,内核调度线程以及线程间竞争资源带来的代价也在逐渐增加,因此当线程数超过某一阈值,系统的处理能力反而有所下降。 在高速实时系统要求快速响应、频繁分配、高并发的背景下,本文在Buddy算法的基础上,提出一种无锁内存分配算法LFMA,通过渐进式重合并算法提高了在频繁相似大小内存分配情况下的分配效率。无论在单线程还是多线程情况下,LFMA的分配效率都有所提高。但是,本文算法在内存总量过大时会造成位图长度较大或内碎率过高的问题,下一步的研究计划是将内存进行区块划分,在每一个区块上分别调用LFMA算法来解决上述问题。2 无锁内存分配算法
2.1 LFMA算法
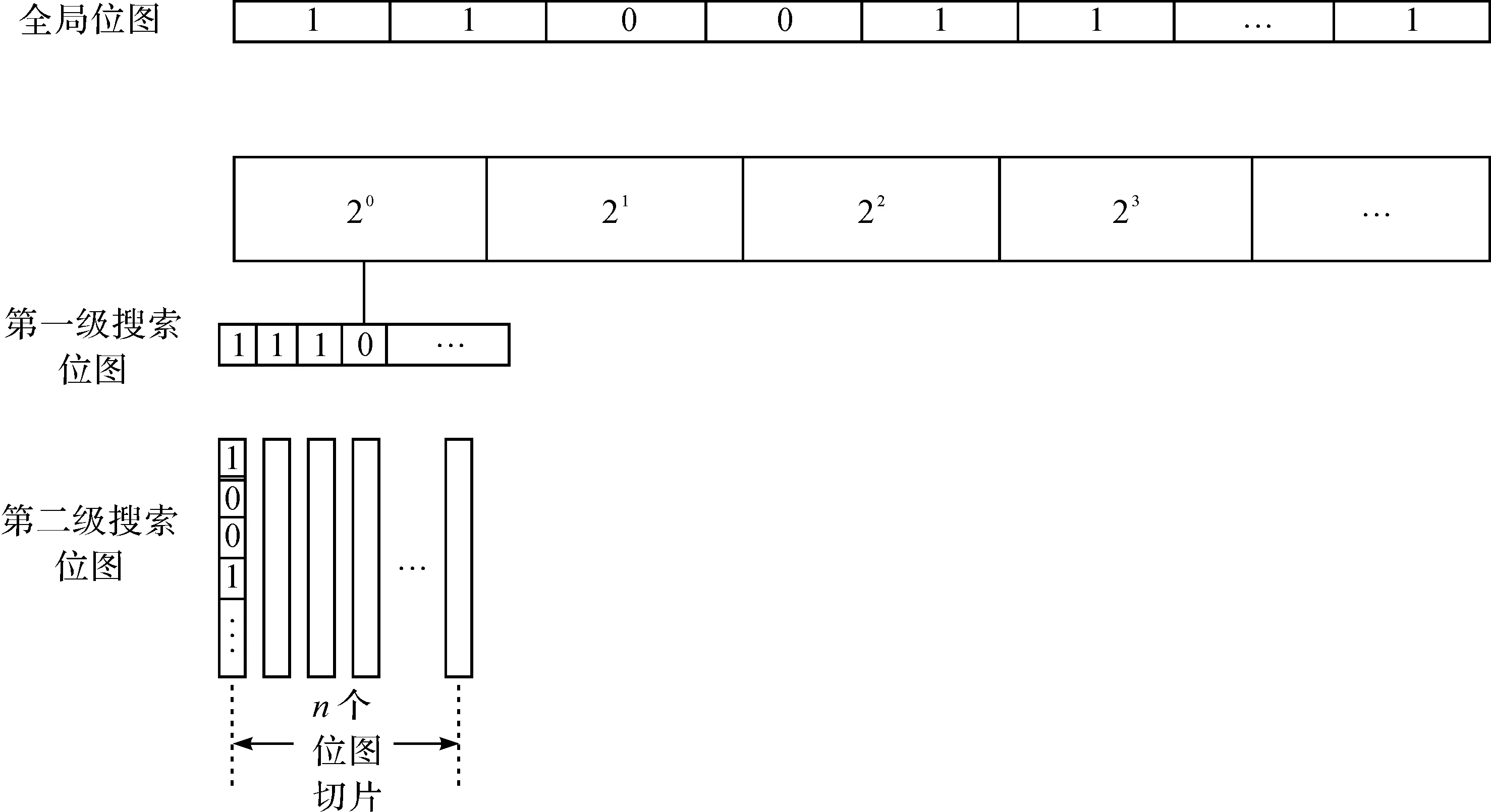
2.2 多级位图的原子操作

2.3 渐进式重合并算法
3 实验设计与分析
3.1 实验设计
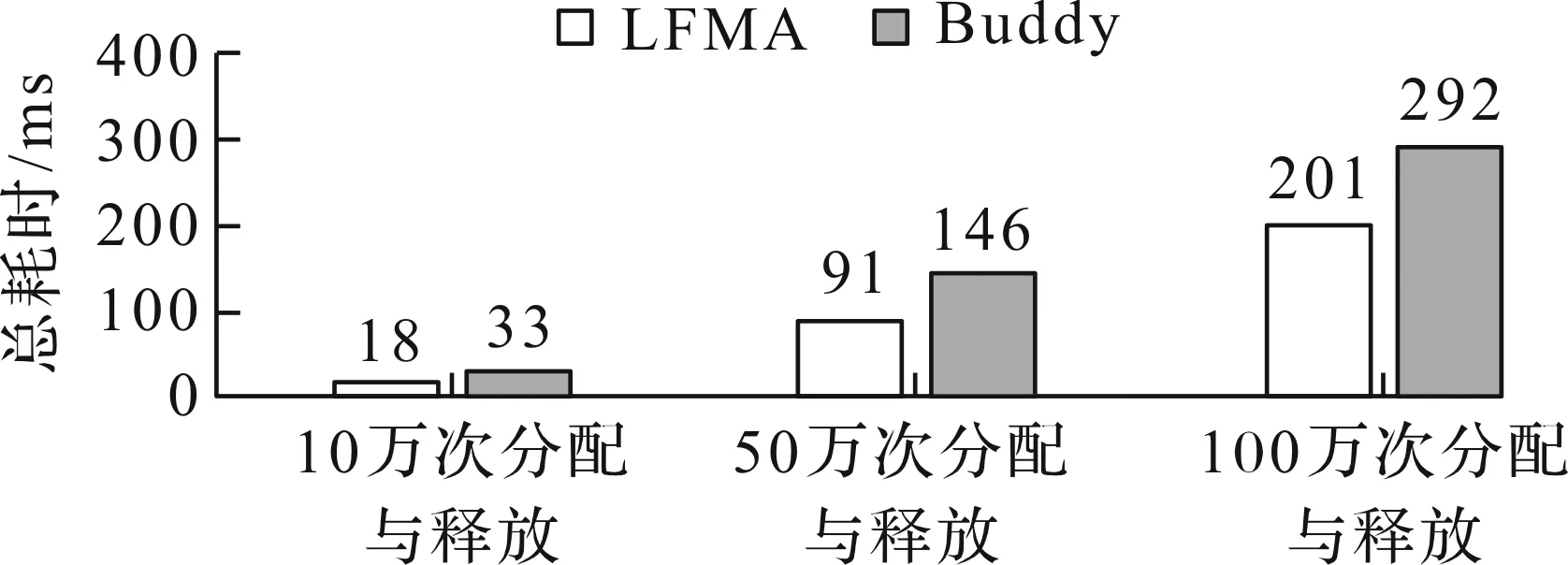
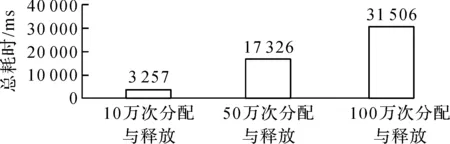
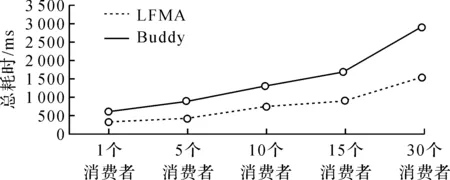
3.2 实验结果与分析

4 结束语

