非均匀外载下弯曲井眼中含缺陷套管抗挤强度计算新模型
胡旭光 胡光辉 何 焱
(1.中国石油集团川庆钻探工程有限公司钻采工程技术研究院,四川 广汉 618300;2.国家能源高含硫气藏开采研发中心,四川 成都 610051;3.四川长宁天然气开发有限责任公司,四川 成都 610056)
0 引言
套管作为油气井钻完井工程中的重要一环,入井前须根据井下工况对套管进行校核以确保套管入井后其抗挤强度满足开采需要,确定更全面、精确的套管抗挤强度计算公式,也成为国际学者研究的重点之一。随着钻井向深井超深井发展,对套管的抗挤强度要求已经成为套管选型的决定性因素。国际标准化组织ISO 颁布了套管抗挤强度计算标准[1],但该标准在计算时将斜井也视为直井,未考虑井眼曲率的影响。当井眼曲率较小时,其对套管抗挤强度的影响可忽略不计,仍可按照直井计算,但当井眼曲率较大时其套管抗挤强度迅速下降,若仍按照直井计算,将导致计算值远远大于实际值,带来严重的后续影响。目前国际上尚未针对井眼曲率对套管抗挤强度计算公式进行修正,国内专家及学者对此研究也较少,虽然已有高校考虑井眼曲率影响后开展了一些研究[2],但研究时将套管质量假设为理想状态,未考虑本身制造缺陷(不圆度、壁厚不均度等)的影响,与实际情况有偏差,计算结果不够精确。为此,综合考虑套管所受非均匀外载、井眼曲率及制造缺陷(不圆度、壁厚不均度)的影响,建立非均匀外载下弯曲井眼中含缺陷套管抗挤强度计算新模型,更符合井下套管实际情况,可为井下套管抗挤强度的精确计算提供参考。
1 套管抗挤强度公式的建立
1.1 非均匀外载下理想套管抗挤强度计算公式
下套管、注水泥至候凝结束后,水泥环将地层与套管连接成为一个整体,依据弹塑性力学理论,固井后套管受力可简化为平面应变问题[3]。若不考虑制造缺陷(不圆度、壁厚不均度等)的影响,井下套管受力模型见图1。

图1 理想套管的力学模型图
设其应力函数为:

式中,φ为应力系数,无因次;r为套管外径,mm;θ为所受外载与水平方向之间的夹角,°;A、B、C、A1、B1、C1、D1为应力系数,无因次。
根据弹塑性力学理论,Cr2lnr=0,即C=0。

式中,σr为径向应力,MPa;σθ为周向应力,MPa;τrθ为切应力,MPa;θ为井眼曲率,rad/m。
边界条件为:

式中,r1为椭圆短轴,mm;r2为椭圆长轴,mm;q1为短轴方向载荷,MPa;q2为长轴方向载荷,MPa。
边界条件为:

由边界条件可得A、A1、B1、C1、D1的表达式如下:

式中,Kr=r1r2。
套管在地层中的受力情况简化成平面应变问题后,对应的Von Mises屈服准则可表示如下:

套管屈服首先发生在r=r,θ=0 或π/2 处,由式(1-2)、(1-3)得

将公式(11)、(12)代入公式(10),即可推导得到非均匀外载作用下无制造缺陷的套管抗挤强度计算公式:
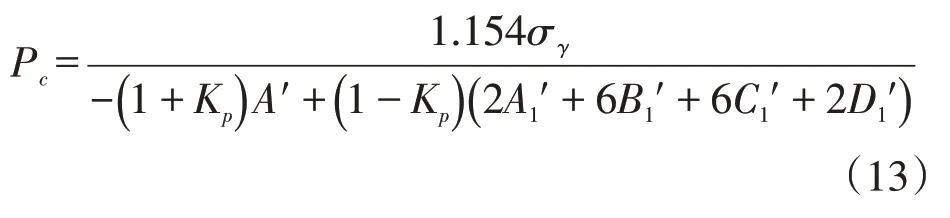
1.2 考虑制造缺陷后对公式进行修正
公式(13)未考虑套管自身缺陷对抗挤强度的影响,计算值偏大。而由于制造工艺水平限制,固井时使用的套管并非理想体,生产过程中不可避免会存在壁厚不均度、不圆度及残余应力等制造缺陷。而已有研究表明制造缺陷对套管性能的影响不可忽略,尤其在地层条件复杂时,必须将其作为套管强度校核时需考虑的因素[4-7],API 5C3 计算公式未考虑套管自身制造缺陷对抗挤强度的影响[8],若继续按照API 5C3给出的标准计算套管抗挤强度将导致计算精度出现不同程度的下降[9-15],对于地层条件复杂的情况将导致严重的套管挤毁事故。针对此种情况国际标准化组织(ISO)综合考虑不圆度、壁厚不均度、残余应力及制造工艺的影响,建立了此种前提条件下的计算公式。

根据公式(14)对公式(13)进行修正,得出修正后的计算公式为:

1.3 考虑井眼弯曲后对公式进行修正
公式(15)的前提条件为直井,未考虑井眼曲率对抗挤强度的影响。井眼曲率会引起套管径向受力和轴向受拉,导致其抗外挤能力下降。中国石油大学黄根炉教授在研究井眼曲率对抗挤强度影响时,提出了弯曲应力影响系数Kz,即

式中:D为套管外径,mm;E为杨氏模量,取值为206.9× 105MPa。
弯曲应力会导致套管抗挤强度降低,因此建立公式时可认为弯曲应力降低了套管屈服强度进而降低其抗挤强度,将作为套管屈服强度影响系数,则将Kz代入公式(15),即可得考虑井眼弯曲后含缺陷套管抗挤强度计算新公式:

式中,χ=0.127e+0.03 9ε-0.44( )σr σγ+hn;e为套管不圆度,为壁厚不均度,σ为残余应力,MPa;h为应力应变rn系数,hn=0.017。
式(17)即为本文建立的套管抗挤强度计算新模型。
2 公式准确性验证
由于实验条件限制,通过室内挤毁试验来获取弯曲井眼套管抗挤强度难度很大,为验证自建的新模型的整体准确性,拟通过以下方法验证自建新模型的准确性。首先,设定计算参数后对比自建的公式、黄根炉教授建立的弯曲井眼套管抗挤强度公式计算值、ISO公式计算值,验证三者计算值变化趋势是否一致,若一致,可判断自建的公式与套管实际抗挤强度变化值相吻合;其次,通过有限元模拟软件对弯曲井眼中含缺陷套管进行模拟,并将自建的公式、黄根炉教授建立的弯曲井眼套管抗挤强度公式计算值、ISO公式计算值分别与有限元模拟结果进行对比,判断自建的公式是否更接近于有限元模拟值,若更接近有限元模拟值,则说明自建的公式可用于弯曲井眼套管抗挤强度计算。
2.1 有限元模拟
以外径177.8 mm,壁厚12.65 mm,最小屈服强度965 MPa 套管为模拟对象,建模时套管长度取1 m,根据套管出厂实际情况其不圆度设为1.5%,壁厚不均度设为12.5%。建立三维有限元模型(图2)。
建模时在通过以下方式模拟套管弯曲:一端施加约束,另一端施加弯曲载荷F,F根据公式(18)求出。


图2 弯曲井眼中套管有限元模型图
式中,F为弯曲载荷,N;E为套管弹性模量,取值为 2.06 × 105MPa;I为套管截面惯性矩,(D4-d4),m4;d 为套管内径,mm;θ为端面转角,rad;L为套管长度,m。
2.2 模拟值与理论值的对比
对套管受力情况进行有限元模拟时,为防止边界效应对模拟结果造成影响,取套管中间截面的von Mises 应力为研究对象,认为当套管中间截面von Mises 应力最大值达到套管最小屈服强度(965 MPa)时,套管所受外载为其当前的抗挤强度,按照此方法即可模拟出在不同参数下的套管抗挤强度值(图3)。
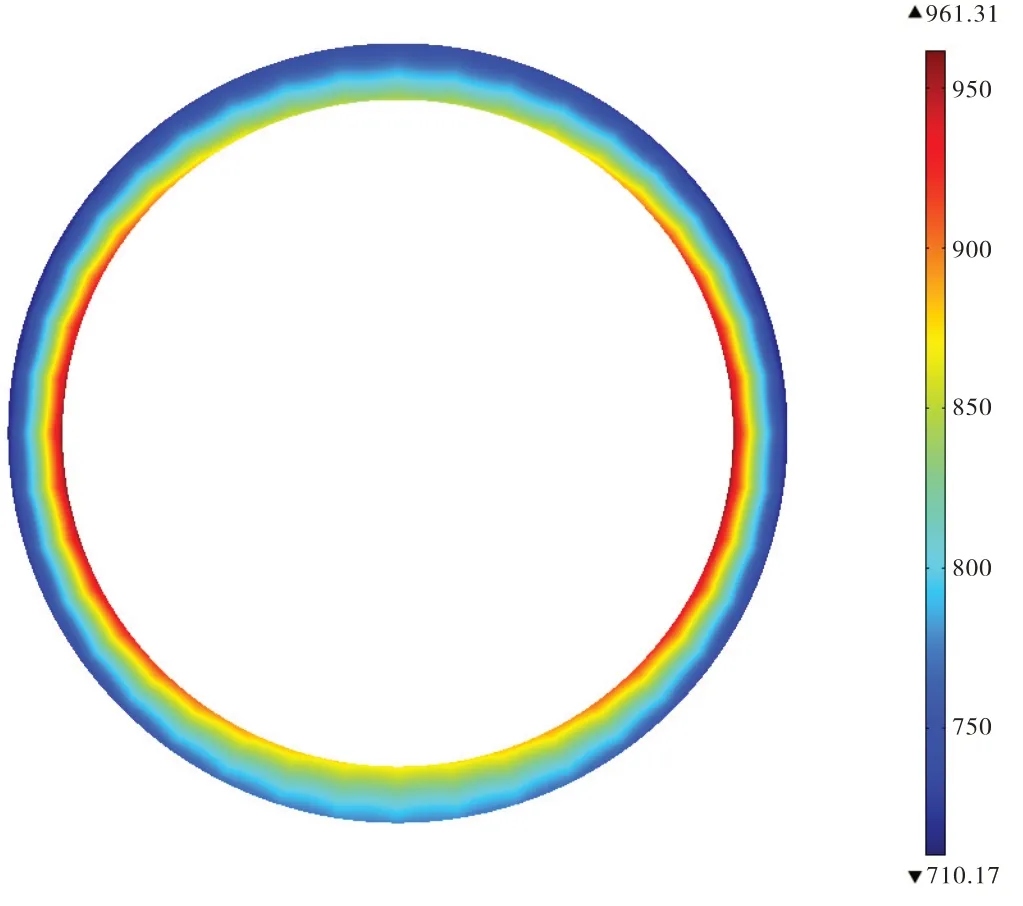
图3 套管中间截面von Mises应力图
建立三维模型时设定井眼曲率为30°/100 m,保持其他参数不变,模拟外挤力不均度为1、0.9、0.8、0.7、0.6、0.5 时的套管抗挤强度,并与自建公式计算值、黄根炉公式计算值、ISO公式计算值进行对比(图4)。

图4 三种公式计算结果与有限元模拟值的对比图
由图4可以看出,自建公式计算出的抗挤强度值变化趋势与黄根炉教授建立的弯曲井眼套管抗挤强度公式计算值、ISO公式计算值的变化趋势一致,且更接近有限元模拟值,能反映出自建公式的正确性及计算精度。
建立三维模型时设定外挤力不均度为0.8,保持其他参数不变,模拟井眼曲率分别为10°/100 m、20°/100 m、30°/100 m、40°/100 m、50°/100 m时的套管抗挤强度,并与自建公式、黄根炉建立的弯曲井眼套管抗挤强度公式计算值进行对比(图5)。由于ISO 公式未考虑井眼曲率的影响。因此没有与ISO公式计算值进行对比。

图5 两种公式计算结果与有限元模拟值的对比图
由图5可以看出,自建公式计算出的抗挤强度值变化趋势与黄根炉教授建立的弯曲井眼套管抗挤强度公式计算值的变化趋势一致,且更接近有限元模拟值,能反映自建公式的正确性及计算精度。
3 结论
1)在ISO 给出的套管抗挤强度计算公式及前人研究基础上,综合考虑套管受到的非均匀外载、自身制造缺陷、井眼曲率对抗挤强度的影响,建立了弯曲井眼中套管抗挤强度计算新公式,更符合井下套管实际情况。
2)通过对比自建公式计算出的抗挤强度值与黄根炉教授建立的弯曲井眼套管抗挤强度公式计算值、ISO公式计算值,得出在同样参数条件下三种公式计算值的变化趋势一致。
3)通过有限元软件建立了弯曲井眼套管三维模型,将模拟值分别与自建公式计算值、中国石油大学黄根炉教授建立的套管抗挤强度公式计算值、ISO公式计算值进行对比,自建公式计算值更接近有限元模拟值;
4)三种计算公式计算值的变化趋势及其与模拟值的对比能反映出新模型的正确性及计算精度,可用于弯曲井眼中套管抗挤强度的计算。

