行程敏感式液阻减振器动力学特性的三维流-固耦合有限元仿真分析

徐文雪，吕振华

(清华大学车辆与运载学院，北京 100084)

车辆悬架系统中的液阻减振器是用于改善车辆行驶平顺性的重要功能部件，传统的被动式液阻减振器在结构方案确定之后，其阻尼特性仅与速度相关，而行程敏感式减振器的阻尼特性不仅与速度相关，同时还受活塞行程/位置的影响[1]。常见的行程敏感式减振器的形式有：缸壁槽形[1−2]、附加阀式[3]、附加回油通道式[4]等。缸壁槽形行程敏感式液阻减振器在与主活塞平衡位置相对应的缸筒内壁上开设一个或多个浅槽，通过增大局部行程的通流面积实现对阻尼力的衰减。

设计手册文献[1]中给出了缸壁槽形行程敏感式减振器在不同活塞偏置状态下的示功特性，并对其具体应用前景给出一些工程性建议，即比较适用于具有车身高度控制的车辆，如卡车的驾驶室悬架及装配有空气弹簧的公共汽车悬架系统。文献[2，5 − 6]采用一维流体分析软件建立了行程敏感式双筒减振器的集总参数模型，探讨了缸壁槽结构参数对示功特性及流量特性的影响。文献[7]建立了缸壁槽形行程敏感式减振器的集总参数模型，用驾驶员座椅和后排座椅处的加速度响应信号评价了装有行程敏感式减振器的车辆的减振效果。这些研究局限于固定振幅、低速工况的减振器阻尼特性的计算分析，且不能给出减振器内部流场的三维瞬态特性。

上述集总参数模型不能用于研究缸壁槽截面形状及分布对行程敏感式减振器的阻尼特性及其内部流场动力学特性的影响，因此，需采用基于结构有限元分析(FEA)、计算流体动力学(CFD)和流-固耦合(FSI)动力学的数值仿真分析技术，以实现行程敏感式减振器内部工作过程流-固耦合动力学响应特性的三维仿真分析[8]。文献[9]采用同步化迭代流-固耦合计算方法分析了减振器的板阀式补偿阀的结构对减振器空程性畸变的临界速度的影响；文献[10]采用交错迭代流-固耦合计算方法对减振器的弹性阀片式节流阀系的动态特性进行了仿真分析；文献[11 − 12]采用直接流-固耦合方法对减振器的锥形节流阀系的耦合自激非线性振动现象进行了仿真分析；文献[13 − 14]采用迭代流-固耦合计算方法对半主动液阻减振器的动态特性进行了仿真分析。直接流-固耦合算法采用有限元方法求解结构及流体方程，耦合边界上的结构和流体变量同步求解，不存在时间滞后及能量不守恒现象，但与某些流体算法(如滑移网格流-流耦合算法)无法兼容；同步化迭代流-固耦合算法采用预估-迭代方法，相对于交错迭代流-固耦合算法具有更高的计算精度和稳定性。

本文建立了一种具有缸壁槽形行程敏感式可变阻尼特性的单筒充气式液阻减振器的较精细的三维流-固耦合有限元仿真分析模型，采用同步化迭代流-固耦合动力学计算方法及滑移网格流-流耦合计算方法，求解减振器在简谐激励、冲击激励下的三维流-固耦合动力学响应，探讨减振器的高速动力学特性及活塞偏置或缸壁槽结构改变后减振器的阻尼特性的变化规律。

1 行程敏感式减振器流-固耦合有限元分析模型构建与求解

1.1 流-固耦合有限元模型构建方法

本文所研究的缸壁槽形行程敏感式减振器的结构简图如图1(a)所示，缸壁槽结构及分布如图1(b)所示，3 组浅长槽在缸筒内壁均匀分布，每组含有3 条半径为2 mm 的半圆柱形槽，将其分别标记为S、M、L。当主活塞运动至缸壁槽长度范围内，压缩室与伸张压缩室内油液亦可通过缸壁槽流通，引起伸张及压缩阻尼力值减小。

流-固耦合动力学仿真分析过程计算量较大，而本文所设计减振器结构具有1/3 对称性，故为保证单元质量及模型计算精度并提高计算效率，采用1/3 部分模型进行流-固耦合动力学计算分析。首先，建立行程敏感式减振器的简化结构几何模型，结构所围封闭空间即为流体几何区域，其可通过Boolean 运算获得。本文结构及流体的有限元网格模型如图2 所示。在结构模型中，较复杂的主活塞结构采用四面体网格，活塞杆、阀板及浮动活塞结构均采用六面体网格。流体模型采用全六面体网格，阀板与主活塞间预留一定间隙，用于模拟阀板开启后所形成的缝隙通道；在间隙处划分四层六面体单元，以满足阀板开启过程中的网格变形需求；缸壁槽内流体单独划分六面体网格，不必与大流场内流体网格满足共结点条件，并采用较小尺度网格以捕捉槽道内的流场特性；与缸壁槽相连通的大流场区域也采用较小尺度网格，以保证滑移网格耦合方法的计算精度；在压力场、速度场变化剧烈的阀系附近采用较小尺度网格单元，在压力场、速度场分布较均匀的大流场内采用较大尺度网格单元即可。

图2 液阻减振器系统的有限元网格模型Fig. 2 FE meshed model of a DS damper system

在流-固耦合有限元模型中，定义阀板外表面、流道内表面、浮动活塞与油液的接触表面和主活塞的上、下表面为流-固耦合边界；定义与缸筒接触的流体表面为固定壁面边界；定义阀板与主活塞表面为接触面；用弹簧单元代替压紧弹簧的实体结构，其弹性特性如图3 所示；不建立气室内气体的网格单元，代之以弹簧单元，反映气体P-V关系，如图4 所示；结构材料为钢，油液为一种液压油，具体材料参数如表1 所示。

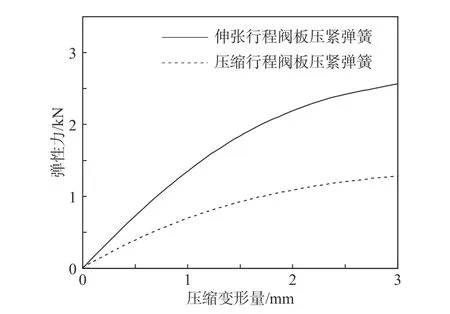
图3 压紧弹簧弹性特性Fig. 3 Spring Stiffness

图4 气室内气体P-V 关系Fig. 4 P-V curve of gas in chamber

表1 材料参数Table 1 Material parameters

缸壁槽形行程敏感式减振器流-固耦合有限元模型构建的难点在于缸壁槽道内流体与压缩室、伸张压缩室内流场的瞬时连通与截断过程的仿真分析。采用流体的滑移网格(Sliding Mesh)耦合方法来实现不同区域流场间的耦合作用，将缸壁槽内流体与压缩室、伸张压缩室内流体进行虚拟分割，将两区域的分割面定义为一组滑移网格耦合边界。

1.2 流-固耦合有限元模型求解方法

流-固耦合系统的求解涉及到固体、流体及流-固耦合边界处控制方程的求解[15]，其中固体的弹性动力学方程为：

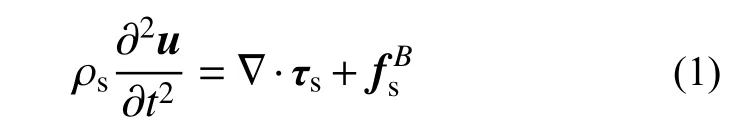
式中： ρs为固体密度；u为固体的变形量；τs为柯西应力张量；fsB为固体的体积力；t为时间。油液在Euler 坐标系下的守恒型N-S 控制方程为：

在行程敏感式减振器工作过程中，主活塞驱动流体通过阀系及缸壁槽，产生动力耦合作用，其流-固耦合有限元模型的求解涉及到ALE 流-固耦合、滑移网格流-流耦合、流场动网格控制等算法。

可以采用同步化迭代耦合计算方法来求解流-固耦合模型方程，其求解流程如图5 所示。

图5 同步化迭代流-固耦合计算流程图Fig. 5 Procedure of synchronous-iterative FSI computation

流体的滑移网格耦合方法将计算区域分成两部分，两区域交界面处的网格结点可相互独立，通过两区域边界处变量当前值的内插值来保证缸壁槽内流场与所连通的大流场间压力、速度等场量的实时连续性。

在流体模型中，采用主-从结点(Leader-Follower)方法进行动网格的控制，以保证计算过程中流体模型的网格质量。

1.3 模型验证

对本文所设计的行程敏感式减振器进行多工况性能测试，减振器的主要结构参数如下：缸筒内径和主活塞直径为80 mm，主活塞上开有直径8 mm的流通孔12 个(双向各6 个)；阀板的直径均为72 mm，厚度均为3 mm，由蝶形弹簧压紧。阀系和带缸壁槽的缸筒如图6 所示。实验测试设备如图7 所示，具体测试工况如表2 所示。激励方式为作用于活塞杆端部的正弦波激励，主活塞初始位置位于缸壁槽中点处。

图6 实验加工实物Fig. 6 Components of DS damper

图7 实验测试设备Fig. 7 Test bench

对上述实验对象进行流-固耦合仿真分析。提取计算结果中活塞杆的端面载荷以得到减振器的示功特性，表2 中工况的实测与计算结果如图8所示。

表2 实验测试工况Table 2 Test conditions

图8 减振器示功图Fig. 8 Work diagrams of damper

由图8 可以看出，流-固耦合仿真分析结果与实验测试结果具有较好的一致性，验证了流-固耦合有限元模型的建模及求解方法的有效性。

2 行程敏感式减振器的流-固耦合动力学特性及阻尼特性仿真分析

2.1 行程敏感式减振器的高速动力学响应

基于流-固耦合模型可进行减振器高速阻尼特性及内部工作过程动力学响应预测，对指导高速减振器设计具有重要意义，仿真分析工况如表3所示。

表3 仿真分析工况Table 3 Simulation conditions

对上述工况进行仿真计算，得到减振器在工况1-1～工况1-6 下的减振器示功特性及阻尼力-速度特性，如图9 所示；在工况2-1～工况2-6 下的减振器示功特性及阻尼力-速度特性，如图10 所示。在图9、图10 中标示出阻尼力随缸壁槽依次开启、关闭的变化过程，垂直的虚线代表减振器主活塞的中截面，主活塞总厚度为20 mm，但缸壁槽处主活塞厚度仅为16 mm，其一端距中截面10 mm，另一端距中截面6 mm，故示功特性并非关于位移行程中点对称分布。

在图9、图10 中，发现高速工况中缸壁槽在被开启、关闭的瞬态过程中阻尼力值出现明显波动，以伸张行程为例，将每次波动的峰值标记为A、C、E、I、K、M，将每次波动的谷值标记为B、D、F、H、J、L。后续将结合减振器流场的动态特性对此现象进行综合分析。

图9 减振器阻尼特性(较小振幅)Fig. 9 Damping characteristics (small amplitude)

图10 减振器阻尼特性(较大振幅)Fig. 10 Damping characteristics (large amplitude)

将图10 中伸张行程中不同活塞速度幅值下缸壁槽在特征点A时刻的阻尼力值FA与特征点G时刻的阻尼力值FG列于表4 中，并计算二者的阻尼力差值 ∆F及下降比例 η1( =|FA−FG|/|FA|×100%)，以探讨不同的活塞速度幅值下缸壁槽对减振器阻尼力特性的影响。

表4 特殊点处的阻尼力值Table 4 Damping forces at special points

由表4 可以看出，缸壁槽对减振器阻尼力的衰减比例随活塞速度幅值的增大而减小，即激振速度越低，缸壁槽对阻尼力的衰减越大，这是不利的。

进一步获取减振器的流场动态特性分布，探讨其与减振器阻尼特性的相互联系，揭示缸壁槽形行程敏感式减振器的工作机理，以工况1-6(速度幅值3 m/s，位移幅值32 mm)为例，图11 为减振器阀系附近流场的压力分布，图12 为阀系附近流场的速度分布，图13 为缸壁槽通道出口处截面的压力分布云图。

由图11 可以看出，减振器流场在阀系附近压力梯度较大，离阀系较远处压力梯度较小，且缸壁槽内压力与大流场内压力连续性很好，证明了滑移网格耦合方法的有效性。在缸壁槽关闭时刻，缸壁槽内流场压差较大；在压缩行程中缸壁槽关闭时刻，缸壁槽内流场出现负压区，这是由于流-固耦合计算中未考虑空化效应。

由图12 可见，在压缩行程、伸张行程的活塞最大速度时刻，流场的最大流速均发生在缸壁槽内，其值分别达67 m/s、90.5 m/s。结合图13 可见，缸壁槽内流体中心流线压力较低，槽道流体速度分布不均，中心位置流速较高；大部分流体一直运动至槽道末端才进入大流场。

为进一步通过流场的动态特性分布来探讨图9(a)中阻尼力值发生波动现象的原因，获取该减振器在特征点A、B、C、D时刻主活塞上阀系两侧截面和缸壁槽进口(主活塞上沿(U)对应截面)、出口(主活塞下沿(L)对应截面)的压强分布如图14所示，主活塞流道和缸壁槽内速度分布如图15 所示，阀板开度特性如图16 所示，流量特性如图17所示。

将图16 中伸张行程阀板开度的第一次波动的峰值，谷值标记为X、Y、Z，其位置与伸张行程缸壁槽开启导致的阻尼力波动的峰值、谷值间存在一定时间差；压缩行程阀板的压紧弹簧刚度较小，导致压缩行程阀板开度较大，波动程度较弱。

以图9(a)中伸张行程阻尼力值的第一次波动处的特征点A、B、C、D及图16 中伸张行程阀板开度的第一次波动处的特征点X、Y、Z为研究对象，综合考虑减振器的阻尼、压差、流量、流速特性，对缸壁槽形行程敏感式减振器在特定工况下所产生的阻尼力值波动现象进行解释。具体结果列于表5 中。

由表5 可以看出，从特征点A时刻到特征点C时刻，缸壁槽L 已开启，缸壁槽S、M 仍关闭，阻尼力值先减小后增大，与节流阀两侧压差变化规律一致，缸壁槽L 进、出口截面间压差逐渐增大，槽内流体最大流速逐渐增大，阀板开度变化相对阻尼力值变化存在一定时间滞后，活塞的伸张行程流道内流量变化规律与阀板开度变化规律一致；在特征点C时刻，缸壁槽M 也开启，缸壁槽L 内流体的截面压差和最大流速开始减小，但由于缸壁槽M 开启，缸壁槽总流量增大，其它参数变化规律则与特征点A时刻到B时刻的变化规律一致。

图11 阀系附近压力场Fig. 11 Liquid pressure distribution around valve

图13 缸壁槽通道出口处截面的压力分布云图Fig. 13 Pressure distribution in groove-path exits

2.2 行程敏感式减振器的冲击动力学特性分析

进一步探讨路面冲击载荷作用下行程敏感式减振器的动力学响应。假定车辆行驶经过一个200 mm 半径的半圆形凸坎，车轮轮心的运动包络轨迹如图18(a)所示(车轮半径548 mm，不考虑车轮弹性)。

通过某越野车辆的双横臂悬架的运动学模型获得车轮轮心点跳动量和减振器的压缩/伸张变形量之间的比值为2.04，由此得到减振器活塞的压缩-伸张位移量与凸坎宽度间的关系。假定车辆行驶经过该凸坎的速度为40 km/h，则通过凸坎的时间约为0.09 s。车轮上跳对应于减振器的压缩行程，活塞杆的位移、速度时间历程曲线如图18(b)、图18(c)所示。

将图18 所示的运动激励加载到减振器的流-固耦合有限元模型，计算得到行程敏感式减振器的冲击动力学响应特性，图19 为减振器的阻尼特性曲线，图20 为缸壁槽内和阀系附近流场在典型时刻的速度分布图。

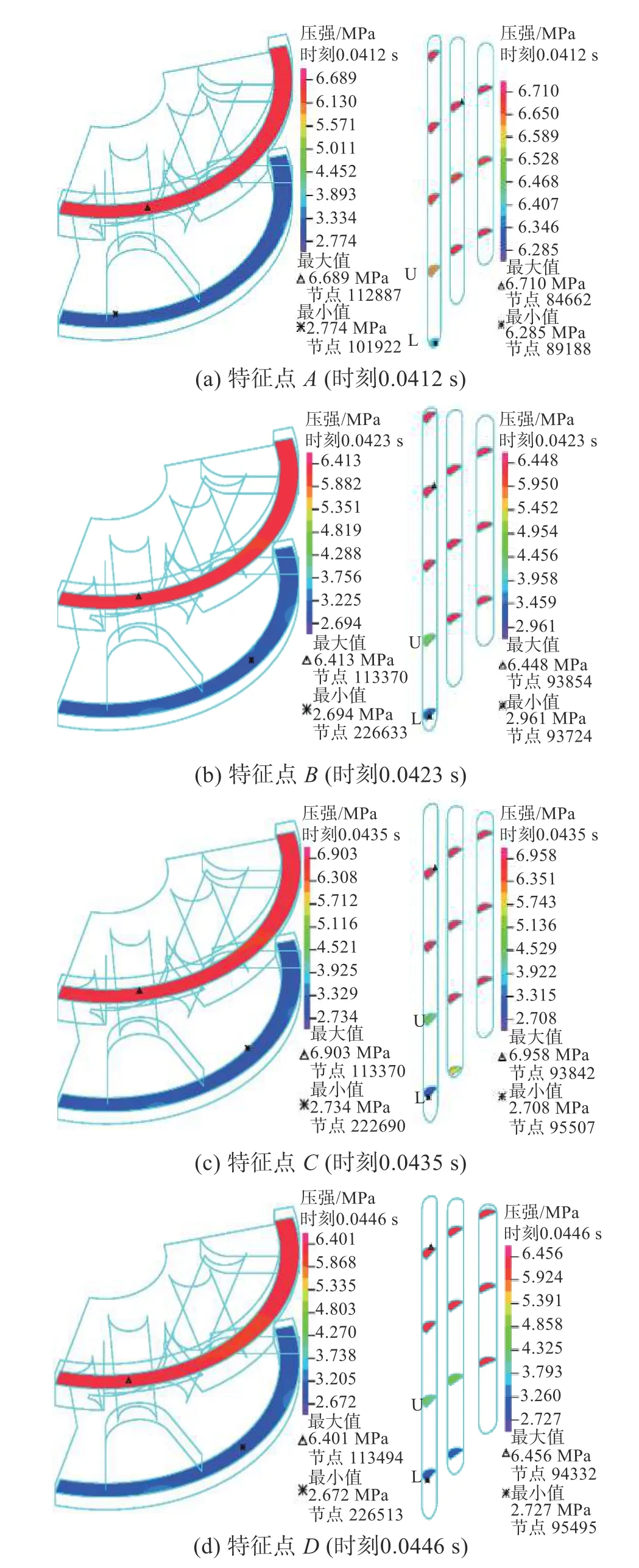
图14 截面压强分布特性Fig. 14 Liquid pressure distribution within cross sections

图15 速度分布特性Fig. 15 Liquid velocity distribution

在图19 中标示出缸壁槽内最大流速点时刻，缸壁槽S、M、L 依次关闭时刻的阻尼力值A′、B′、C′、D′。当车轮行驶进入凸坎时，减振器主活塞速度迅速增大，缸壁槽内流体速度高达98.5 m/s，阻尼力值从A′点开始不增反降到B′点，削减了阻尼力的瞬间冲击峰值；缸壁槽依次关闭后，减振器恢复到主活塞阀系节流状态。而对于正常设计的普通减振器，在遇到强冲击时会发生阻尼力过大的现象，易造成对车身的强冲击以及阻尼节流阀的损坏。

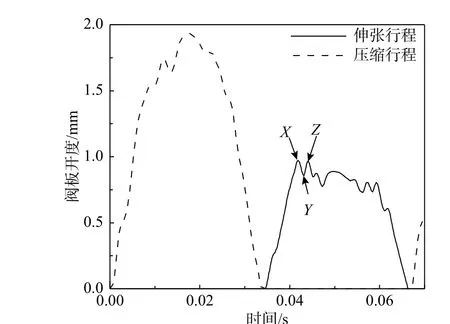
图16 阀板开度-时间历程Fig. 16 Valve clearance time history

图17 流量特性Fig. 17 Valve flow rate time history

表5 减振器流-固耦合响应量Table 5 FSI responses of damper

图18 减振器输入函数Fig. 18 Input excitation to damper

2.3 活塞偏置时行程敏感式减振器的阻尼特性分析

在实际工作过程中，车辆负载变化等因素会导致主活塞的静平衡位置偏离缸壁槽中间位置。图21 为主活塞沿压缩行程方向偏置时的减振器的示功特性和阻尼力-速度特性。

图19 减振器阻尼特性Fig. 19 Damping characteristics

图20 速度分布图Fig. 20 Liquid velocity distribution

由图21 可以看出，当活塞沿压缩行程方向偏置时，阻尼力值在压缩行程初期增长较慢，可减小对车身的冲击；活塞经过压缩行程最大速度点后，阻尼力衰减较慢，可充分发挥其衰减振动的作用；阻尼力值在伸张行程初期增长较快，可迅速衰减振动；活塞经过伸张行程最大速度点后，阻尼力值衰减较快，此为缸壁槽相对活塞偏置后的一点不利影响。总体而言，活塞沿压缩行程方向偏置的状态是有利的，可成为进行减振器的压缩-伸张行程的不同阻尼特性匹配的一个措施；而活塞沿伸张行程方向偏置的状态则是不利的；不同的偏置量所导致的减振器阻尼特性也各不相同。

图21 活塞偏置时减振器的阻尼特性Fig. 21 Damping characteristics with piston offset

2.4 缸壁槽的分布及结构对行程敏感式减振器阻尼特性的影响

本节探讨缸壁槽的分布及结构对行程敏感式减振器的输出特性的影响。逐步改变减振器的缸壁槽数目及组合，得到减振器在工况1-4(活塞速度幅值2 m/s，活塞位移幅值32 mm)下的示功特性如图22 所示。

由图22 可以看出，以伸张行程为例，单缸壁槽形行程敏感式减振器的阻尼力只在缸壁槽开启及关闭时存在两次波动，缸壁槽开启后，减振器阻尼力变化规律基本一致；两缸壁槽形行程敏感式减振器的阻尼力在两条缸壁槽分别开启及关闭时存在四次波动，两条缸壁槽全部开启后，减振器阻尼力变化规律基本一致；三缸壁槽形行程敏感式减振器的阻尼力存在六次波动，并表现出单条缸壁槽作用结果的叠加效应。提取普通减振器和三缸壁槽形行程敏感式减振器的示功特性中主活塞最大速度点处的阻尼力值F1、F2，并计算缸壁槽所引起的阻尼力下降比例 η2( =|F1−F2|/|F1|×100%)，具体结果见表6。

图22 多个缸壁槽道分别对示功特性的影响Fig. 22 Influence of multi-grooves to work diagram

由表6 可以看出，行程敏感式减振器对伸张行程阻尼力的调节作用强，对压缩行程阻尼力的调节作用弱；由流场的压力分布可获得缸壁槽内流体进口和出口截面间的压差在伸张行程活塞最大速度点处为1.25 MPa，在压缩行程活塞最大速度点处为0.8 MPa，压差越大，缸壁槽对阻尼力的影响越大。

表6 不同减振器的阻尼力值对比Table 6 Comparison of damping forces

在原缸壁槽结构基础上加长其过渡段长度，以使得缸壁槽流道被开启、关闭过程的通流面积及阻尼力变化更加平缓，具体结构如图23 所示。

图23 缸壁槽修改方案 /mm Fig. 23 Modification of grooves

滑移网格耦合方法的采用使得流-固耦合计算过程中只需重新划分缸壁槽内流体的网格单元，而无需对其它流场单元进行处理，有利于提高仿真模型重构效率。对局部修改了的缸壁槽形行程敏感式减振器的流-固耦合仿真模型在工况1-4(速度幅值2 m/s，位移幅值32 mm)及工况2-2(速度幅值1 m/s，位移幅值48.5 mm)下进行求解，其示功特性如图24 所示，可见阻尼力的波动明显减弱了。

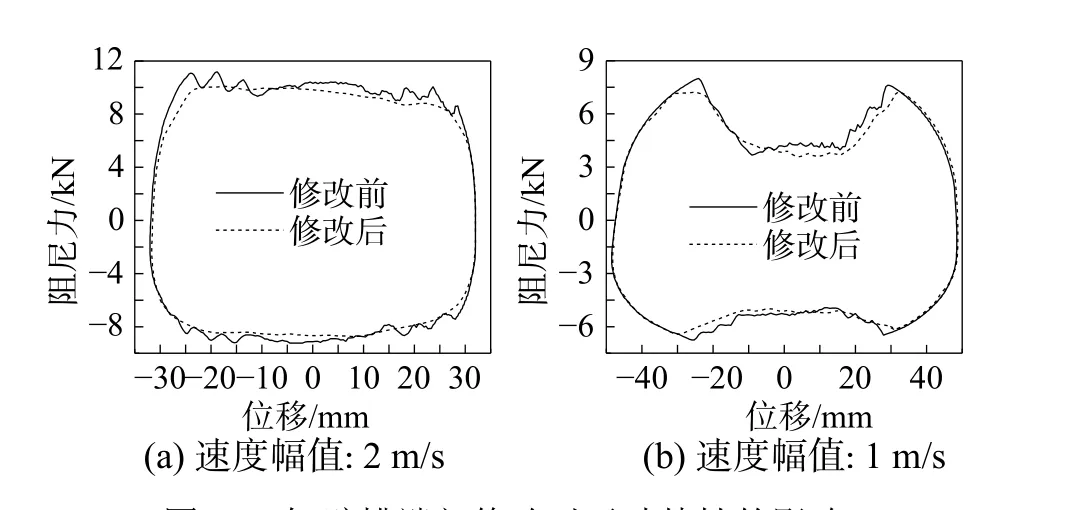
图24 缸壁槽端部修改对示功特性的影响Fig. 24 Influence of groove modification on work diagrams

3 结论

本文建立了缸壁槽形行程敏感式液阻减振器的三维流-固耦合有限元仿真分析模型，探讨了减振器的高速动力学特性、冲击动力学特性及活塞偏置或缸壁槽结构改变后减振器的阻尼特性的变化规律，可得以下结论：

(1)基于ALE 流-固耦合、滑移网格流-流耦合、流场动网格控制的同步化迭代流-固耦合计算方法可精确求解缸壁槽形行程敏感式筒式液阻减振器的复杂三维流-固耦合有限元模型，实现内部流场动力学特性和减振器变阻尼特性的仿真分析，具有重要的学术意义与技术价值。

(2)仿真分析结果表明：活塞沿压缩行程方向偏置时，阻尼力在压缩行程初期增长缓慢，可减小对车身的冲击，而在伸张行程初期增长较快，可迅速衰减振动，这可成为进行此类液阻减振器的压缩-伸张行程的不同阻尼特性匹配的一个有利措施，而活塞沿伸张行程方向偏置的状况是不利的；在地面冲击工况下，缸壁槽的附加泄流作用可削减阻尼力的瞬间冲击峰值，减小对车身的强冲击，并有利于防止阻尼节流阀系的冲击损坏。

(3)仿真分析结果还表明：多缸壁槽形行程敏感式减振器的阻尼特性表现出单条缸壁槽作用结果的叠加效应；缸壁槽对减振器阻尼力的衰减比例随活塞速度幅值的减小而增大；缸壁槽在高速工况下被开启及关闭的瞬态过程中伴随有阻尼力波动现象，可通过适当延长缸壁槽端部收缩段加以改善。