滞后阻尼体系地震反应的中心差分虚初始条件法
祁文睿,潘旦光,2,高永涛,付相球
(1. 北京科技大学土木与资源工程学院,北京 100083;2. 城市地下空间工程北京市重点实验室,土木与资源工程学院,北京科技大学,北京 100083)
阻尼为系统的固有特征,对结构的动力反应有显著影响。根据材料的耗能特性,可建立相应的阻尼模型[1]。对于土木工程而言,粘滞阻尼和滞后阻尼是两个广泛使用的模型。粘滞阻尼力与速度成正比,具有计算简便的特点而成为广泛使用的模型[2],如Rayleigh 阻尼模型和速度相关型的阻尼器[3−5]。但是,粘滞阻尼的耗能和频率相关。已有实验表明,很多材料的耗能与频率无关,如型钢混凝土梁[6]、土[7−8]和粘弹性夹层梁和板[9−10]等,此时采用阻尼力与位移成正比相位差π/2 的滞后阻尼模型更符合实验结果。滞后阻尼将导致复刚度运动方程,而常采用频域方法进行求解。频域计算方法以Fourier 变换为基础,理论上仅适用于线弹性体系,对于非线性系统,常采用等效线性化进行计算[11−13]。为进行真非线性计算,需要在时域中进行直接积分法进行计算。
为在时域中进行复本构运动方程的求解,朱镜清[14−15]、何钟怡[16]等根据对偶原则,建立与实荷载对应的对偶虚荷载,完善了滞后阻尼体系的输入理论。但是,采用时域直接积分法计算滞后阻尼体系动力反应,即使是无条件稳定的直接积分方法也易于出现发散的结果[17−19]。微分方程数值解不稳定的原因有两种:一种是数值方法的不稳定;另一种是由于方程本身具有发散解。复阻尼运动方程的逐步积分法的发散解是由后一种原因造成的[17,20]。为使复阻尼运动方程的逐步积分法计算结果稳定,一种常用的方法是将滞后阻尼等效为近似的粘滞阻尼[21−22],但计算结果的误差较大。
在直接积分法得到滞后阻尼体系稳定解方面,孙攀旭等分别基于激励插值方法[23]和滞变阻尼时域理论[24],建立了稳定的直接积分计算方法。事实上,滞后阻尼体系的特征值为互为相反数的复数特征对[25],必然有一个特征值的实部是正的,由此导致强迫荷载下补解中的一项是没有物理意义的发散项,在解析解时人工删除发散项而使计算结果稳定。而直接积分法的计算结果是包含补解的,且滞后阻尼体系直接积分法是收敛到包含发散项补解[17]而导致计算结果不稳定。Pan 等[26]首先提出虚初始条件的概念,然后基于无条件稳定的Newmark 法建立使滞后阻尼直接积分解不出现发散项的计算方法。本文进一步建立了恒载下的虚初始条件,以及基于有条件稳定的中心差分法建立滞后阻尼的中心差分虚初始条件法。在此基础上,通过算例验证验证所提方法的稳定性、计算精度和计算效率。
1 滞后阻尼体系的虚初始条件
1.1 自由振动

1.2 简谐荷载作用
在简谐荷载Aeiθt作用下,单自由度体系的运动方程为:


1.3 恒载作用

1.4 地震作用
若已知地面运动加速度为a(t),将a(t)采用Fourier 级数展开:


2 虚初始条件的中心差分计算方法
若已知tn时刻及以前时刻的反应已知的情况下,根据中心差分法,求解tn+1时刻的位移方程为:



表1 任意荷载下中心差分虚初始条件法计算步骤Table 1 Calculation procedure of central differential virtual initial condition method under arbitrary load
3 算例
为验证本文算法的有效性,下面以文献[17]分析过的算例进行本文算法的验证。已知体系的滞后阻尼系数η=0.1,对无阻尼自振频率f=0.1 Hz、1 Hz、10 Hz 的三个体系进行地震反应计算。以表2中的3 条地震波分别作为体系的地震输入。输入地震波的加速度时程如图1 所示。在进行中心差分法计算时,根据中心差分法的稳定性条件和输入地震波的采样时间间隔,计算时间步长 ∆t取为:

式中:Tn为体系的自振周期;Δts为地震波加速度时程的采样时间间隔。

表2 地震波主要参数Table 2 The main parameters of ground motions

图1 输入地震波的加速度时程Fig. 1 Acceleration time histories of input seismic waves
作为对比,对地震作用形成式(31)的方程后,计算各项简谐荷载的解析解并求和,所得结果作为解析解。当u(0)=u0,u˙(0)=v0时,位移、速度和加速度的解析解为:


利用式(46)进行Fourier 逆变换,可得位移、速度和加速度的频域解为:
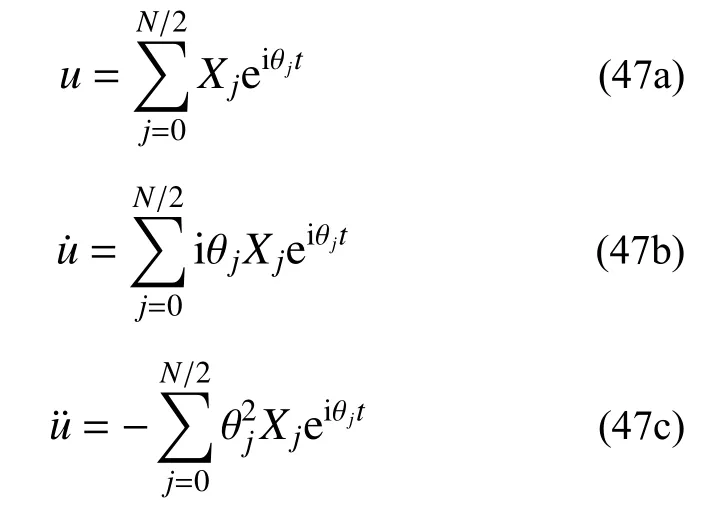
对比式(44)和式(47)可知,解析解包括由初始条件引起的自由振动,由荷载引起的伴生自由振动和荷载所引起的纯强迫振动。而频域解仅包含荷载所引起的纯强迫振动。
当u0=v0=0,f=10 Hz 时,三条地震波作用下体系的位移反应如图2 所示,f=10 Hz 时天津波作用下的速度和加速度反应如图3 所示,f=1 Hz 和0.1 Hz 时天津波作用下的位移反应如图4 所示。

图3 天津波作用下的速度和加速度反应(f=10 Hz, u0=v0=0)Fig. 3 Velocity and acceleration response under Tianjin wave excitation
由图2~图4 可知,对于不同的地震输入和自振频率体系,中心差分虚初始条件法计算的位移、速度和加速度都和解析解基本一致,计算结果稳定而不存在临界自振周期的问题[17]。而对于频域解,当f=10 Hz 时与解析解几乎重合;当f=0.1 Hz 时,频域解与解析解存在明显差别。这是因为频域解得到的是体系的稳态反应,而解析解是包含稳态和伴生自由振动的瞬态反应,自振频率越高,瞬态反应衰减越快,因此,对于自振频率较高的体系,瞬态反应对体系的总反应影响很小而可直接采用稳态解进行描述,但是,对于自振频率低的体系,瞬态反应衰减需要较长的时间,当自振周期和地震波持时为同一量级时,则瞬态反应在整个地震反应过程中都有显著影响,此时采用仅包含稳态解的频域分析方法将产生显著误差。本文所提的中心差分虚初始条件法,计算结果包含瞬态反应和稳态反应,对于不同自振周期体系的反应都和解析解吻合的很好。

图2 三条地震作用下位移反应(f=10 Hz, u0=v0=0)Fig. 2 Displacement responses under three seismic excitations(f=10 Hz, u0=v0=0)

图4 天津波作用下不同自振频率体系的位移反应(u0=v0=0)Fig. 4 Displacement response for various natural vibration frequencies under Tianjin wave excitation
当体系初始条件非零时,在天津波作用下不同自振频率的位移反应如图5 所示,f=10 Hz 体系的速度与加速度反应如图6 所示。初始条件非零情况与零初始条件下的计算结果对比可知,由于初始位移和初始速度瞬态振动的进一步影响,导致频域解在初始阶段误差增大。对于自振频率较高的10 Hz 体系,由于瞬态振动很快消失,此时忽略初始条件对体系总反应的影响较小。但是对于自振周期与输入地震波持时为同一量级的0.1 Hz 体系,初始位移和初始速度引起的瞬态振动将对总反应产生显著影响,此时忽略初始条件将引起显著误差。

图5 天津波作用下不同自振频率体系的位移反应Fig. 5 Displacement response of various natural vibration frequencies under Tianjin wave excitation
为定量研究不同方法的精确性,不同方法相对解析解的峰值相对误差为:

式中: |r∗(t)|max表示精确解的峰值; |r(t)|max表示近似解的峰值。

图6 天津波作用下体系的速度和加速度反应(f=10 Hz)Fig. 6 Velocity and acceleration response under Tianjin wave excitation
零初始条件下本文方法及频域解的峰值相对误差如表3 所示。由表3 可知,当体系的自振频率较高时,频域解的计算精度高;而当体系的自振频率较低时,频域解将产生显著误差;而中心差分虚初始条件法对于不同自振周期体系反应的峰值相对误差都小于5%,显示了良好的精度。
表4 为u0=v0=0,f=1 Hz 时,天津波作用下三种方法位移反应的计算时间。解析解为输入地震波的Fourier 变换时间和式(44a)各项直接求和的计算时间,中心差分虚初始条件法的计算时间包括输入地震波的Fourier 变换时间、计算虚初始条件的时间和每个时刻位移、速度和加速度的递推计算的时间,频域法则为Fourier 变换和Fourier 逆变换的总时间。在进行解析解计算时,由于自由振动和伴生自由振动的影响,无法采用快速Fourier变换进行计算而采用逐项求和,因此,计算时间最长。频域采用快速Fourier 变换,计算时间最短。中心差分虚初始条件法通过前一步的计算结果递推后一步的计算结果,计算效率仅次于频域方法,且计算时间显著小于解析解。结合表3 和表4 的数据分析结果表明,中心差分虚初始条件法兼顾了计算精度和计算效率。

表3 本文方法与频域解的峰值相对误差Table 3 Peak relative errors of the proposed method and frequency domain solution

表4 不同算法计算时间比较 /sTable 4 Comparison of calculation time of various methods
4 结论
针对滞后阻尼体系直接积分法收敛到包含发散项而不稳定的问题,提出了中心差分虚初始条件计算方法。由理论分析和数值计算结果可知:
(1)对于不同峰值加速度、卓越频率的地震输入,及不同自振频率体系,本文所提的中心差分虚初始条件法对位移、速度和加速度均能得到稳定的计算结果,不存在临界自振周期的问题。实初始条件是可观测和测量部分,虚初始条件是伴随实初始条件而存在的,可无需人为干涉而使滞后阻尼体系计算结果稳定。由此进行直接积分法计算,即使有条件稳定的中心差分法,依然可以得到稳定的计算结果。
(2)对于自振频率较高的体系,瞬态反应对体系的总反应影响很小而可直接采用稳态解进行描述,而对于自振频率低的体系,如自振周期和地震波持时为同一量级时,瞬态反应在整个地震反应过程中都有显著影响,此时采用仅包含稳态解的频域分析方法将产生显著误差。
(3)中心差分虚初始条件法的计算结果包括瞬态反应和稳态反应,计算误差和体系的自振频率无关,可适用于不同的自振频率体系。
(4)中心差分虚初始条件法计算的峰值相对误差小于5%。同时,计算时间显著小于解析解,因此,这种方法兼顾了计算精度和计算效率。

