基于NSRFG 方法的标准地貌风场大涡模拟研究

胡晓兵，杨 易

(华南理工大学亚热带建筑科学国家重点实验室，广东，广州 510641)

计算流体动力学(Computational Fluid Dynamic,CFD)越来越多地被用于解决计算风工程问题，如建筑环境中的污染物扩散、自然通风、行人风舒适性、建筑结构风荷载等[1−4]。其中，大涡模拟(LES)因其能提供高分辨率的流场时空信息，应用越来越广泛。LES 中入流湍流的准确模拟，是计算风工程领域当前研究的热点；准确定义与各类地貌大气边界层真实湍流特征相符的入流边界条件，是进行建筑结构风效应研究的前提，也是计算风工程LES 研究的难题之一[5]。

目前，计算风工程中LES 入口湍流生成方法主要分为三大类[6−7]：1)前导数据库法(Precursor Simulation Methods)；2)循环法(Recycling Methods)；3)湍流合成法(Synthetic Turbulence)。前两种方法属于“被动式”入口湍流生成方法，难于控制湍流强度、湍流积分尺度、功率谱等流动参数，且需要消耗大量的计算时间及存储空间。湍流合成法属于“主动式”模拟方法，是近年来LES 入口湍流生成问题的研究热点，主要分成四种：1)谐波叠加法(Weighted Amplitude Wave Superposition Method，WAWS)，能够生成满足功率谱和互谱的湍流场，但WAWS 生成的湍流场不能满足零散度的条件，因此可能无法确定生成的流场的连续性条件；2)数字滤波法(Digital Filter Methods)，其通过过滤随机速度场在空间和时间产生相干结构。该方法的主要限制是不能自动满足零散度速度场条件，需进行修正以避免流域中的伪压力波动；3)合成涡方法(Synthetic Eddy Methods, SEM)，基于涡旋叠加产生速度波动，但同样也不能保证零散度速度场；4)随机湍流生成方法(Random Field Generation，RFG)，该方法由Kraichnan[8]于1970 年首先提出，而后在2001 年Smirnov 等[9]通过对谐波函数叠加产生的连续流场进行缩尺和正交变换，建议了满足高斯谱的RFG 方法；2010 年后又发展了DSRFG 法[10]、改进的DSRFG 法[11]、CDRFG 法[12]。

2018 年，Yu 等[13]在以上研究基础上，提出一种改进的入口湍流生成方法NSRFG(Narrow Band Synthesis Random Flow Generation)方法，可严格保证入口湍流满足连续性条件，且计算精度和效率相对此前的RFG 系列方法得到较大提高，是计算风工程领域LES 数值模拟中较有前景的一种入流湍流模拟方法。

本文基于NSRFG 方法编制MATLAB 程序，采用数值分析对若干参数进行了敏感性研究，分析了其对湍流脉动风速功率谱、均方值和空间相关性等的影响；然后，参考有关规范，建议了一套与我国现行建筑结构荷载规范四类标准地貌风场相对应的参数取值表；最后，通过实例对四类标准地貌的大气边界层湍流风场进行了数值模拟和平衡态检验，为在计算风工程领域采用LES NSRFG 方法进行结构风工程一般问题的数值模拟研究提供参考。

1 NSRFG 湍流合成法

NSRFG 方法[13]对“谐波单元”时程表达式进行重新构造，使各参数的取值具备明确的理论依据。通过时域叠加的方法重构满足要求的单点脉动风速时程，再由单点扩展到三维空间，从而构造出满足大气边界层零散度、空间相关性和脉动风速功率谱等湍流特征的脉动风速场，实现对LES 入口湍流速度场更精确高效地模拟。NSRFG方法数学模型如式(1)所示：

1.1 脉动风速功率谱特性

脉动风速功率谱表示脉动风的能量在频率域中的分布情况。对于大气边界层湍流风场，可采用von Karman 谱反映脉动风速的统计特性，三个方向的脉动风速谱表达式如下：

1.2 空间和时间相关性

脉动风速的空间相关性是检验模拟的湍流风场的关键指标之一。由式(1)求出空间上任意两点时程的空间相关函数，如式(5)所示：

将式(5)求得的三维方向上空间相关性与理论目标函数比较。空间相关性的目标函数采用Hémon 和Santi[15]提出的公式：

脉动风速的时间相关性反映了湍流涡结构的大小。与空间相关性类似，NSRFG 方法生成的湍流风场的时间相关函数，由式(7)计算：

轮滑运动中，学生往往忽略防护装备的重要性，经过对于轮滑爱好者的调查中能够发现，约有75 %的轮滑运动者未曾进行防护用具的使用，26 %的轮滑运动者佩戴头盔保护头部不会受到伤害；13 %的轮滑运动者佩戴护肘保护肘部，同时，调查发现佩戴防护用具的大部分是老年轮滑运动者，在青年轮滑运动者中无人佩戴防护用具，因此导致大部分因轮滑运动受伤的运动者都是青年人，以上调查现象能够表明，不使用防护用具能够加大受伤的几率。

2 参数敏感性分析

NSRFG 方法理论模型中参数众多，如何采用数值分析方法进行合理设置参数以准确模拟目标湍流风场需要进一步探讨。为此，首先参考中国规范的C 类地貌，并结合欧洲规范(ESDU 85020)有关规定，设计基本数值模型进行湍流风场模拟计算，对NSRFG 模型中若干参数如采样频率间距∆f、引入的时间尺度因子τ0及空间尺度因子θ、衰减系数cj和调谐因子 γj，进行详细参数敏感性研究，分析其对所生成湍流风场的脉动风速均方根、功率谱和空间相关性等结果的影响，得到一般规律性认识；然后，在此基础上建议一套与中国规范四类标准地貌风场相对应的参数表。基本数值模型的参数设置如表1 所示。

表1 基本数值模型湍流风场参数设置Table 1 Parameters of the turbulent wind flow for the basic numerical model

2.1 采样频率间隔Δƒ

真实的湍流总是非均匀和各向异性。本文通过NSRFG 方法的转换和映射技术，以产生具备各向异性特征的脉动风速，模拟得到的三维脉动风速均方根目标值可由各向异性速度相关张量求得，如式(8)所示：

脉动风速均方根代表了湍流风速的波动程度。对于1 m 高度处的监测点，表2 为不同的采样频率间隔 ∆f(功率谱离散数目N)时的脉动风速均方根。从表2 可得，在采样频率fs设定为500 Hz 的情况下，随着 ∆f→0或N→∞时，NSRFG 方法生成的脉动风速均方根越接近均方根目标值。即随着频谱的离散化变得越来越精细，每个频率对应能量包括在生成的时间序列中，模拟结果更准确。

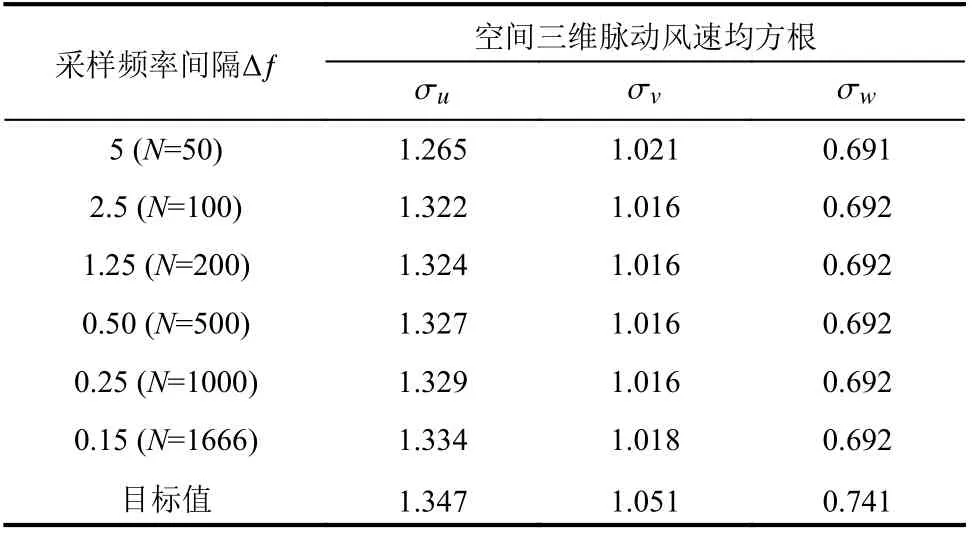
表2 不同采样频率间隔的脉动风速均方根比较Table 2 Comparisons of the RMS values of the fluctuating velocities with different frequency intervals

通过NSRFG 方法生成三维脉动风速时程，把相应的湍流特征参数代入式(4)求出目标功率谱。图1 为具有代表性的3 种不同采样频率间隔Δƒ的1 m 高度处脉动风速功率谱比较。由图1 可知，在采样频率一定的情况下，频率间隔越大，模拟得到的脉动风速功率谱谱值波动幅值越大、越不稳定；频率越小，其值越稳定并与目标功率谱越吻合。图2 为4 种典型的不同频率间隔Δƒ的空间相关性结果比较。图2 表明，在采样频率一定的情况下，频率间距越大，空间两点的空间相关性波动越大，与目标空间相关性偏差也就越大。综合表1、图1 和图2 结果可知，当采样频率间隔∆f=0.25 Hz，即功率谱离散数目N=1000 时，模拟得到的脉动风速统计特征与目标值吻合较好又兼顾计算效率。

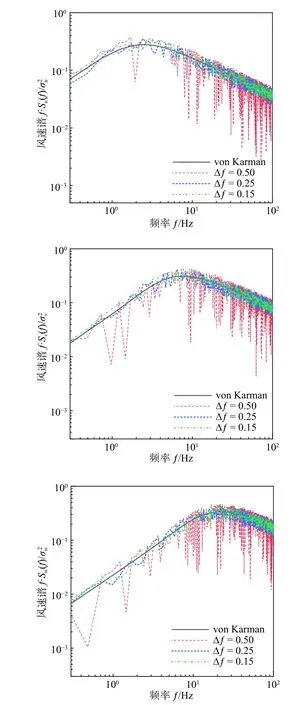
图1 不同采样频率间隔的脉动风速功率谱比较Fig. 1 Comparison of the spectra of the fluctuating velocities with different frequency intervals

图2 不同频率间隔脉动速度的空间相关性比较Fig. 2 Comparison of non-dimensional spatial correlation of the fluctuating velocities with different frequency intervals

2.2 时间尺度因子τ0

参考文献[11]，NSRFG 方法生成湍流风场的三维时间尺度可由式(7)计算得到，并将其与随机平稳过程的自相关函数进行比较，其表达式如下：

式中：Ti(i=u,v,w)是时间尺度。随着时间间隔τ 趋于无穷大，脉动风速中的低频脉动引起零值附近时间相关性的波动；如没有适当的积分上限M0，将无法估计时间尺度。因此，计算中设定当相关性系数第一次穿越零值时，时间尺度的积分运算停止，即确定积分上限M0。NSRFG 方法中三维速度分量时间相关性如图3 所示。

图3 三维脉动速度的时间相关性比较Fig. 3 Comparison of non-dimensional time correlation of the three-dimensional fluctuating velocities

表3 和图4 为在频率间隔 ∆f=0.25 Hz 条件下，选取不同τ0值，湍流场的空间三维脉动风速分量时间尺度Ti的统计结果，分别对应于20 个速度分量序列样本上时间尺度Ti的平均值和均方根。根据Taylor 湍流冻结假设，流场目标时间尺度可通过公式Ti=Li/Uav(i=u,v,w)估算。由图4 可知，运用Taylor 假说得到的流场的时间尺度Ti随着时间尺度因子τ0的增大呈现出线性正相关关系。需要强调的是，在NSRFG 方法中，使用不同的τ0值来适当修正时间尺度，对准确生成流场的目标时间尺度统计特征尤为重要。研究者可参考此方法在更大范围进行时间尺度的研究，以对τ0进行适当调节，获得更准确的模拟结果，见图4。

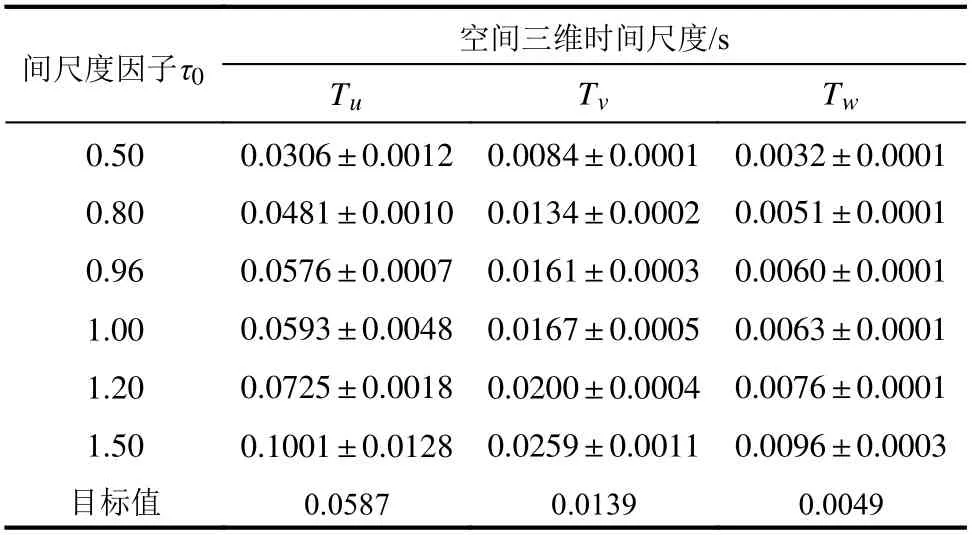
表3 时间尺度统计特性比较Table 3 Comparison of time scale statistics

图4 脉动风速时间尺度随 τ0变化的统计特性Fig. 4 Time scale statistics of the fluctuating velocity as a function of τ0

图5 为在频率间隔 ∆f=0.25 Hz 条件下，不同时间尺度因子τ0下顺风向湍流积分尺度的比较。由图5 可见，时间尺度因子τ0对计算得到的流场湍流积分尺度Lu有着重要影响，其随时间尺度因子τ0的增大而增大。当τ0=1.0时(即不对时间尺度进行调整)，生成流场顺风向湍流积分尺度Lu略大于目标值(表1 给出的湍流积分尺度定义)；而当时间尺度τ0=0.96，生成流场的湍流积分尺度与目标值吻合较好，因此建议时间尺度因子取τ0=0.96。

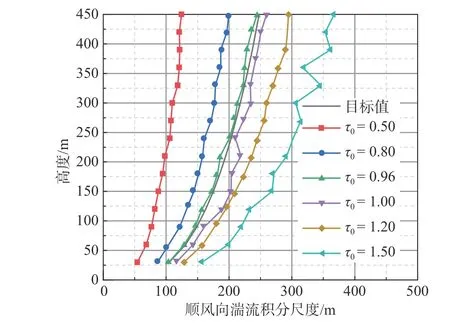
图5 不同时间尺度因子 τ0下的顺风向湍流积分尺度比较Fig. 5 Comparison of longitudinal turbulence integral scales with different time-correlation factors ( τ0)

此外，数值分析表明，时间尺度因子τ0除了对流场时间相关性和湍流积分尺度有影响外，对所生成的湍流风场的空间相关性、湍流强度等其他统计特性影响较小，即可忽略其对湍流强度、空间相关性和脉动风速均方根等的影响。

2.3 空间尺度因子θ

湍流积分尺度表征流场中湍流涡旋的平均尺度，是大气边界层湍流风场的重要统计特性。在NSRFG 方法中，湍流积分尺度作为一个重要参数，对生成流场的湍流特性有着重要影响。由于我国规范尚未给出湍流积分尺度的建议公式，可参考欧洲规范(ESDU 85020)建议的湍流积分尺度经验公式(见表1)。本文在欧洲规范湍流积分尺度经验公式的基础上，引入空间尺度因子θ，对原始公式进行适当修正，以研究湍流积分尺度对湍流风场模拟结果的影响，如式(11)所示：

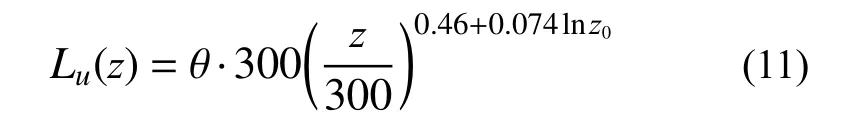
式中， θ为空间尺度因子，用以调节湍流积分尺度进而研究对流场特性的影响。

表4 为 θ不同取值下的采用NSRFG 方法模拟得到的1 m 高度处三维脉动风速均方根比较。由表4 可知，增大空间尺度因子 θ即增大湍流积分尺度，生成的湍流风场各方向脉动风速均方根也随之增大。因此，在NSRFG 方法中空间尺度因子θ即湍流积分尺度对生成湍流风场的脉动风速均方根有着重要影响，需合理确定湍流积分尺度剖面公式，其大小决定了脉动风对结构的影响。

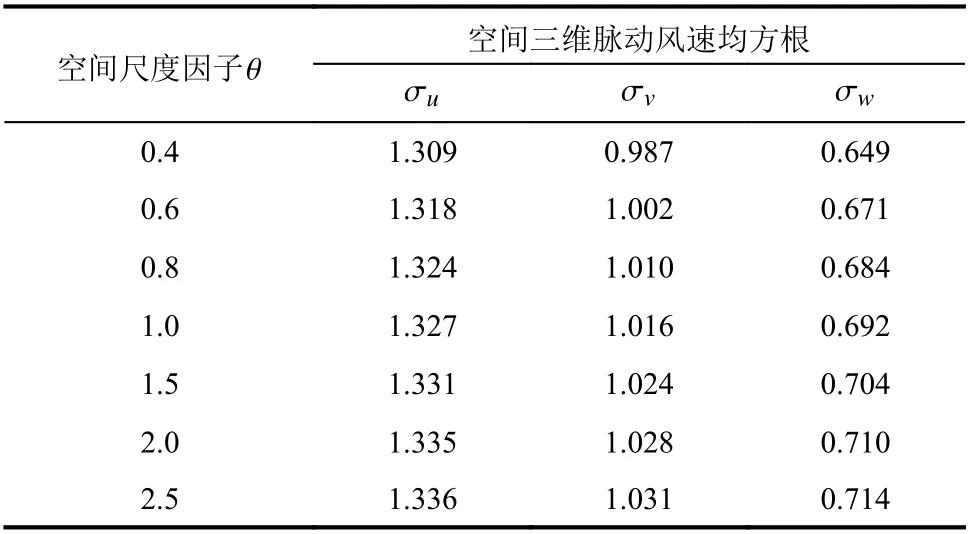
表4 不同空间尺度因子下的脉动风速均方根比较Table 4 Comparison of the RMS values of the fluctuatingvelocities with different spatial scale factors

2.4 调谐因子 cj 及衰减系数γj

NSRFG 方法可通过调整衰减系数cj及调谐因子 γj来保证生成流场的空间相关性。文献[13]只提供其在中国规范(GB 50009−2012)中C 类风场的取值，未给出模拟其余A、B 和D 类地貌风场的参数取值及确定方法。

本文基于NSRFG 方法，按照以上参数敏感性分析方式，通过连续调整衰减系数cj及调谐因子γj进行大量模拟仿真计算，对生成湍流风场的脉动风速功率谱、湍流强度、三维空间相关性曲线等统计特性与目标理论曲线进行逼近，以获得最佳取值，从而得到一套采用NSRFG 方法进行与我国规范相对应的四类标准地貌风场的通用参数取值表，其建议取值在不同几何缩尺比湍流风场模拟计算中同样适用，如表5 所示。需要说明的是，其中时间尺度因子τ0、空间尺度因子θ 统一分别取0.96 和1.0。参考Yang 等[13,17]研究，与A、B、C 和D 类标准地貌相对应的气动粗糙度度z0分别取值为0.01 m、0.05 m、0.7 m、1.0 m。

表5 基于NSRFG 方法的四种标准地貌参数建议值Table 5 Suggested parameters in the NSRFG methods for four standard wind terrain categories

3 平衡态湍流边界层的模拟

采用计算流体动力学方法进行建筑结构绕流风场模拟中，平衡态湍流边界层的模拟是一个重要的前提条件[17]。在前文针对NSRFG 模型中采样频率间距Δƒ、时间尺度因子τ0、空间尺度因子θ、衰减系数cj及调谐因子 γj等影响参数进行探讨的基础上，本节将对以上建议的NSRFG 模型中与我国规范相对应的四类标准地貌风场的数值风场模型，进行平衡态湍流大气边界层风场的数值模拟和检验。

3.1 计算参数与建模

数值模拟采用ANSYS FLUENT 软件平台，基于NSRFG 方法编制UDF 子程序以定义四类地貌大气边界层风场LES 模拟计算的入流湍流边界条件。CFD 模型中计算域尺寸、网格划分和边界条件等，与文献[13]中模拟CAARC 标准建筑模型的空域流场模型保持一致，如图6 所示。数值模拟基于风洞尺度，计算域缩尺比为1∶300，取离地高度0.61m 为参考高度（H），参考高度处的参考风速设置为11.1 m/s（参考风速可自行设定）。计算域采用均匀的正交六面体结构化网格进行划分，并对地面和x=L/3 处(L为计算域顺风向长度)局部网格进行加密，体网格总数约为130 万(见图7)，近壁面y+值约为10～70，适用于壁面函数。考虑到CFL 条件和计算效率，本文时间步长采用0.002 s，模拟时长为25 s，收敛准则定义为速度的绝对残差小于10−5，具体数值求解格式见表6。

图6 LES 计算域、边界条件设置及网格划分示意图Fig. 6 Computational domain, boundary conditions and mesh schemes for LES calculation

表6 LES 计算格式和参数设置Table 6 Calculation formats and parameters in the LES

3.2 模拟结果及分析

3.2.1 平均风速和湍流强度剖面

在计算域x=L/3 处(通常为数值模拟中建筑模型的位置)设置一排竖向监测点，通过模拟得到各监测点的速度时程，进而可以求出平均风速剖面和湍流强度剖面。计算域建筑模型位置处(x=L/3)与入口处定义的理论目标湍流风场特性对比分析如图7 所示，图7 中，Zg为梯度高度，Ug为梯度高度风速，Iu为顺风向湍流强度， α为风剖面指数。

图7 四类标准地貌风场平均风速和湍流度剖面Fig. 7 Mean wind speed and turbulence intensity profiles of four standard wind terrain categories

图7 湍流风场模拟结果显示，对于平均速度剖面，模拟得到的计算域x=L/3 位置的平均风速与入口处的目标速度剖面二者几乎完全保持一致，即速度剖面的保持性良好；而对于湍流强度剖面，x=L/3 位置处的湍流强度剖面相对入口位置目标值略小，这是由于大涡模拟的滤波作用，导致从入口到x=L/3 位置的湍流强度发生衰减。基于湍流合成方法模拟得到的入流湍流的自保持性问题，即高频小尺度湍流衰减，是RFG 方法本身的特性[18−19]，也是本领域的国际性难题，至今尚未完全解决，有待今后继续完善。总体上评价，基于NSRFG 方法和以上建议的参数系，采用数值风洞模拟得到的大气边界层湍流风场基本满足平衡态的要求。

3.2.2 瞬时速度云图

图8 为四类标准地貌下所模拟的大气边界层湍流风场在计算域x=L/3 横截面处的20 s 时顺风向脉动风速瞬时分布云图。由图8 可见，LES NSRFG 方法可以较好重现大气边界层湍流风场不同尺度复杂涡旋结构。

图8 x=L/3 处瞬时速度云图Fig. 8 Instantaneous velocity magnitude contours at x=L/3

3.2.3 纵向脉动风速功率谱

表7 为相应的顺风向脉动风速均方值与目标值的比较，图9 为模拟的x=L/3，z=H处四类标准地貌下大气边界层顺风向脉动风速时程。模拟结果显示，模拟的中国规范四类标准地貌下顺风向脉动风速均方值与目标值的相对误差在5%以内，表明模拟结果与目标值吻合较好。

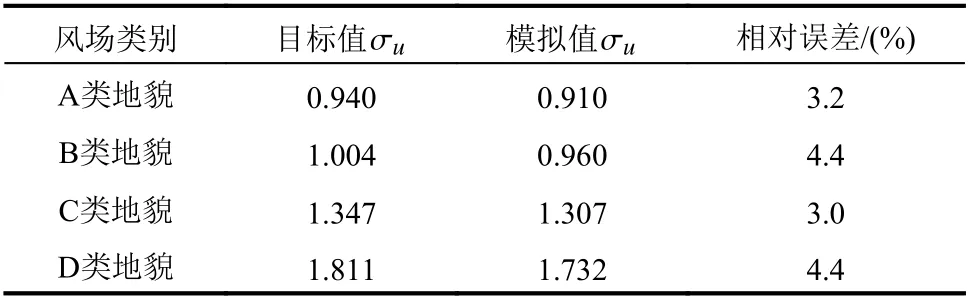
表7 四类地貌顺风向脉动风速均方值与目标值的比较Table 7 Comparison between RMS values of along-wind velocities for the four standard wind terrain categories and target values

图9 模拟的四类湍流风场脉动风速时程Fig. 9 Fluctuating velocity-time histories of four standard wind terrain categories

图10 为NSRFG 方法模拟得到的计算域x=0、L/3，z=H处的顺风向脉动风速功率谱与目标谱(von Karman 谱)的比较。由图10 可知，在入口处(即x=0)，顺风向脉动风速功率密度与Karman 谱吻合较好；在x=L/3 处，顺风向脉动风速功率谱在0 Hz～30 Hz 频率段数值模拟的结果与目标功率谱基本保持一致，而在高频部分由于大涡模拟的滤波作用发生了一定衰减(这是这一类方法的特征，有待今后从RFG 方法本身加以完善)。总体而言，数值模拟的风场能够较好符合目标风场功率谱特性。

图10 四类湍流风场计算域流向风谱与目标谱比较Fig. 10 Comparison between alongwind spectrum of four wind terrain categories in computational domain and the target one

4 结论

入流湍流的准确生成是大涡模拟的关键问题之一，本文基于NSRFG 方法，首先研究了几个重要参数对所模拟风场的湍流特性的影响，建议了与我国规范四类标准地貌相对应的一组参数系，并对四类标准地貌平衡大气边界层进行了模拟。得到以下结论：

(1) 参数敏感性分析发现，重要参数的赋值对湍流风场数值仿真结果影响显著。采样频率间隔∆f的取值越精细，模拟的湍流特性越准确；兼顾计算质量和效率，可取 ∆f=0.25 Hz。通过引入可调节的时间尺度参数τ0和空间尺度因子θ，可对原始NSRFG 方法中时间尺度和湍流积分尺度进行适当修正，以提高湍流风场的模拟精度。

(2) 通过参数敏感性研究和大量模拟仿真分析，本文给出了一组采用NSRFG 方法，模拟与我国建筑结构荷载规范相对应的4 类标准地貌湍流风场的参数表。这个工作相当于基于NSRFG 方法建立了LES 计算的“标准数值风场”模型，为在计算风工程中普及应用LES NSRFG 方法提供参考。

(3) 平衡态边界层风场的CFD 数值模拟验证显示，基于NSRFG 方法模拟LES 入口湍，并适当选取参数，所模拟的湍流风场统计特性整体上可以满足CFD 数值模拟的要求，但在高频段脉动风速功率谱出现一定衰减(该问题与文献中报道类似，这是这一类RFG 方法的特征，有待今后从方法本身加以完善)。未来仍需进一步研究，以改善这一问题，进一步提高基于NSRFG 方法模拟大气边界层湍流风场及建筑结构绕流场的精度。