基于EEP 技术的一维有限元结点位移误差计算

袁 驷，邢沁妍，袁 全

(清华大学土木工程系，北京 100084)

有限元后处理超收敛计算是近年来研究热点之一[1−5]。根据一维有限元的超收敛理论，无论是边值问题的Ritz 有限元还是初值问题的Galerkin有限元的位移解，m(≥1)次多项式单元可得到具有h2m阶的超收敛端结点位移(真解足够光滑)，然而单元内部的有限元解仅为hm+1阶[1−3]。袁驷等[6−9]提出了有限元后处理中超收敛计算的单元能量投影(Element Energy Projection，简称EEP)法，能够计算一维有限元的逐点超收敛解。该技术虽然是基于一维有限元的，但通过一种逐维(dimensionby-dimension，简称D-by-D)恢复策略[10−11]，已经拓展到二维和三维的有限元分析，并应用于多种问题的自适应求解[12−13]。

一维问题的EEP 公式有两种格式：简约格式和凝聚格式[7−9]。二者均被证明可以提供单元内任意点位移及其导数的超收敛解。其中，简约格式的超收敛解精度[14]：位移为O(hm+2) (m>1)，导数为O(hm+1)；凝聚格式的精度[15]：位移及导数均为O(h2m)。EEP 解并不改变单元端结点的位移值，其精度已经很高了，即O(h2m)。然而，更高精度的结点位移对于结点误差估计及其精度提升均具有重要意义。例如，对于初值问题，结点位移精度对于稳定可靠的时程积分是至关重要的，因此，需要有能够对结点位移误差进行有效估计和控制的技术。

本文充分利用EEP 解超收敛特性，提出一种简便有效的结点位移误差计算方法。本法在传统有限元计算后，在不改变现有网格和整体刚度矩阵的情况下，用EEP 解的残余荷载生成新的荷载向量，只经常规的回代过程，即可得到高精度的结点位移误差。再将所估计的误差叠加在传统有限元解，会得到修正的结点位移，其精度具有更高阶的超收敛性：对简约格式有O(h2m+2)精度，对凝聚格式有O(h3m+mod(m,2))精度。例如，对于线性元，修正后的结点位移具有O(h4)精度。此外，由于修正后的结点位移再次具有更高阶的超收敛性，因此可以用其再次改进EEP 解，进而计算另一轮超收敛结点位移。如此反复迭代，最终可获得精确的结点位移，其中每个迭代步的计算量只是荷载向量的生成和回代。

本文以一般的二阶常微分方程为模型问题，给出本法的基本思路和算法，并给出典型算例以展示本法优越的超收敛性以及多样化的拓展和应用。

1 模型问题和EEP 解

1.1 模型问题和有限元解

本文考虑一般的二阶常微分方程边值问题(BVP)和初值问题(IVP)：

式中： ()′=d()/dx；L为式(1)中定义的线性微分算子。不失一般性，以下将u(x)称为位移。对于非自伴情况，其伴随算子为：

定义双线性型和线性型如下：

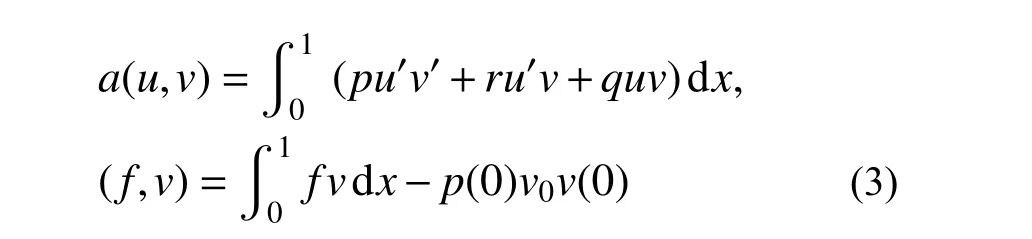
则用常规的Galerkin 位移型有限元求解上述问题归结为求解如下的弱形式问题：

式中：uh∈Sh为有限元解；Sh为m次分段多项式所组成的有限元试探(检验)空间。由vh的任意性，可导出通常意义下的刚度方程：

式中：K为整体刚度矩阵；D为结点位移向量；P为等效结点荷载向量。为方便起见，本文中的“结点”在未特别提及时均指“单元两端结点”，而相应的结点位移表示为uhi。

根据一维有限元误差估计理论，当问题式(1)的解足够光滑且网格足够密(单元长度h足够小)时，由m次元(试探函数和检验函数同次)得到的有限元解在单元端结点上获得O(h2m)[2−3]的超收敛性，而在单元内部则为常规的O(hm+1)[1]的收敛性，即：

式中， ||·||0和 ||·||m+1分别为整个解域上H0和Hm+1范数。式(7)的超收敛阶已经非常高，通常认为是最佳超收敛阶。本文提出用同次单元、同一网格进行另一轮有限元分析而计算出结点位移误差ui−uhi近似解的方法，从而可获得精度更高的结点位移修正解。这一方法关键技术是EEP 超收敛解的应用，将在下一小节中讨论。

1.2 EEP 超收敛解

袁驷等[6]基于结构力学中的矩阵位移法和有限元中的投影定理[1]，提出了一种一维有限元后处理超收敛计算的新型方法，简称为EEP 法[7−9]。本节简要介绍该方法的基本思想和相关公式。

2 结点位移误差的计算

2.1 若干讨论

注意到有限元解uh与EEP 解u∗在单元端结点处相同，即u∗i=uhi，则如果误差e∗=u−u∗可以计算，在端点处e∗i=ehi。因此，用相同网格、同次单元计算e∗的有限元近似解 εh，其结点值 εhi就是有限元结点位移误差的近似解，而且由于其解为结点值，仍具有超收敛性。此为本文的基本思想，简单有效，以下给出具体做法。

2.2 问题提法

2.3 具体算法

3 算法的延伸与拓展

第2.3 节算法是一个基本算法，应用中可以有多种变化和拓展，简述几点如下：

1)结点位移全量。记D(1)=D+δD，算法步骤4)可改为D(1)=K−1(P+P∗)，亦即本法不仅可以计算结点位移增量，也能直接计算修正后的结点位移全量。

2)修正的EEP 解。在求解了 δD得到 εh后，还可以用EEP 法再计算全新的超收敛解 ε∗，此即为u∗的逐点误差估计，从而得到更精确的有限元逐点误差估计eh≈u∗+ε∗−uh。

3)结点的再修正。继得到上述 ε∗后，还可以用本文第2.3 节的算法再计算 ε∗的误差δe∗=e∗−ε∗的近似解 δεh(同时也是修正的位移全量的误差近似解)。 δe∗的定解方程和条件为：

4 数值算例

本节给出若干典型算例，用以验证本法优良的内在特性和多样化的应用场景。本文采用符号计算软件MAPLE 计算，其优点在于用户可以定义数值的字长。

例1. 收敛阶

下面给出数值算例来验证以上的收敛阶。

表1 结点收敛阶(简约格式)Table 1 Nodal convergence orders (Simplified form)

表2 结点收敛阶(凝聚格式)Table 2 Nodal convergence orders (Condensed form)

例2. 反复修正结点

表4 是4 个线性元的结点误差，可以看到网格加密后精度随之提高。而且，尽管没有展示，单元次数更高也会得到更高的精度。

表3 反复修正结点位移Table 3 Repeated nodal value updating

例3. 初值问题的附加精度

本例中，考虑简谐荷载作用下的有阻尼的单自由度体系的运动方程：

对于初值问题，没必要形成整体刚度矩阵，有限元解可以从左到右逐个单元积分求解，因此结点位移修正算法可以逐单元进行，而不用像边值问题待整体求解之后再作修正。如此，对于初值问题，便出现一个增强的修正方法，其特点是在计算单元右端点有限元位移解uh2时，其左端点的初始位移，可以立即采用对有限元解uh1修正后的结点值。这个逐单元修正的方法，不仅更高效，而且结点精度得到进一步的显著提高。

表4 4 个线性元的结点误差Table 4 Errors of nodal values of four linear elements

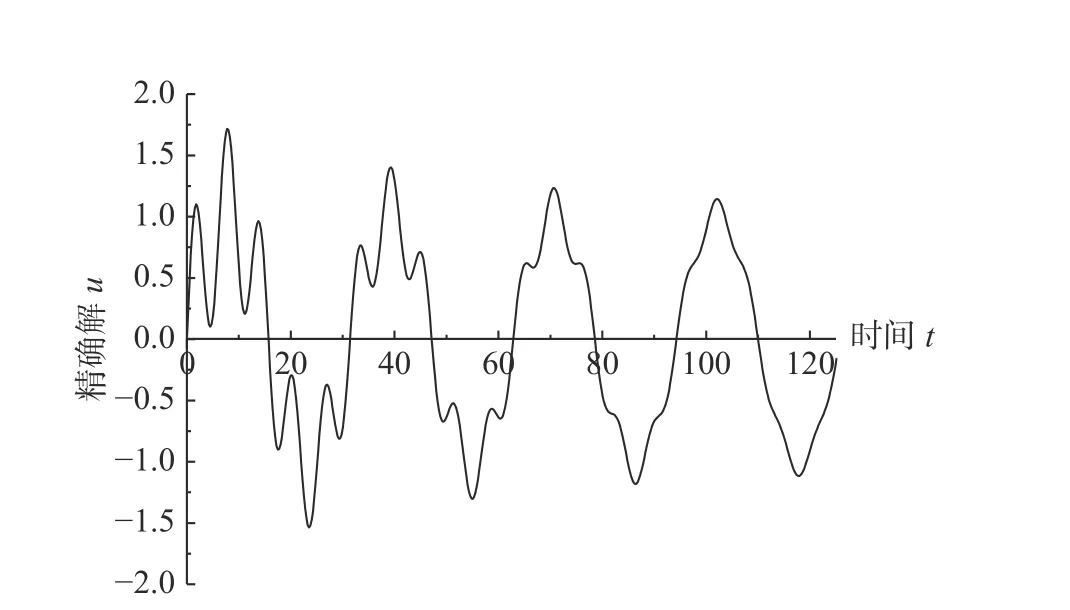
图1 例3 的精确解Fig. 1 Exact solution of Example 3

表5 结点误差和收敛阶( m=1，简约格式)Table 5 Nodal errors and convergence orders ( m=1, simplified form)

图2 有限元解误差Fig. 2 Errors of FE solution

图3 整体修正误差Fig. 3 Errors of globally updated solution

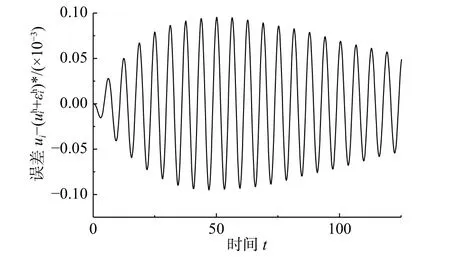
图4 逐单元修正误差Fig. 4 Errors of element-wise updated solution

5 结论

虽然本文的方法和算例主要针对二阶常微分方程，但是所提出的方法也适用于其它一维问题，如其它阶常微分方程问题以及常微分方程组问题。此外，所提出的方法有潜力通过所谓的逐维修正方法扩展到二维乃至三维有限元分析[10−11]。