抑制柱体结构涡激振动的非线性能量阱减振装置优化设计

陈东阳，顾超杰，朱卫军，李迺璐，杨俊伟，芮筱亭

(1. 扬州大学电气与能源动力工程学院，江苏，扬州 225100；2. 南京理工大学发射动力学研究所，江苏，南京 210094)

结构流致振动是有着广泛工程应用背景的流固耦合问题，在航空工程、海洋工程等领域，当流体流过钝体时，钝体下游流场持续产生和脱落旋涡，从而导致结构受到周期变化的流体力作用，使结构以一定的频率和振幅振动，即为涡激振动(vortex-induced vibration, VIV)[1−5]。在流体作用下，当结构振动频率接近结构固有频率时，结构将产生涡激共振，此时振幅将远大于正常情况，并且共振时会发生“频率”锁定现象，在一定来流速度内，结构振动频率都不会发生改变。涡激共振的发生，结构横向上将产生大幅度的振动，受到周期性的疲劳应力作用，从而可能导致钝体结构的疲劳失效，甚至造成对结构的破坏。若结构长期处于频率锁定状态，将大大减少结构的疲劳寿命。

为了减弱涡激振动对高柔性柱体结构疲劳寿命的影响，通常采用主动控制和被动控制来抑制其涡激振动。主动控制[6]通过输入外部能量来扰动流场，如采用声波激励、敲击振动等方式，将旋涡脱落控制在合适情况下，但是该类方法技术含量高，成本也更昂贵。而被动控制通常采用外加控制柱[7]、螺旋列板[8]等扰流装置扰乱流场结构或干扰旋涡的形成与泄放。但这些扰流装置往往会使阻力增大，并且还会引发其他形式的振动。非线性能量阱(nonlinear energy sink, NES)是能实现定向能量传递的具有立方非线性的吸振器[9−12]。NES 通过与柱体共振，将来自柱体系统的振动能量定向传递到吸振器的振子上，并通过阻尼消耗能量，从而达到减小涡激目的[13−14]。NES 不仅具有宽频吸振特性，而且该装置内置于柱体内部，不改变柱体的形状，不会增加额外阻力，成本低。

采用NES 来抑制涡激振动时，不同参数的NES 对柱体振动的抑制效果不同。文献[15 − 17]通常对比不同NES 参数下的涡激振动响应，寻找振动响应与参数间的规律。Mehmood 等[15]使用计算流体力学(computational fluid dynamics, CFD)方法耦合结构动力学建立预测模型，研究NES 的质量比对低雷诺数柱体结构涡激振动的抑制效果。Dai 等[16]采用尾流振子模型研究了NES 作用下的柱体结构频率耦合机理。本人也在前期工作中[17]研究不同NES参数对中等雷诺数柱体结构涡激振动的减振效果。但在实际设计中，人为选取NES 的参数，通常设计出的NES 往往并不能达到最优的抑制效果，同时效率较低。因此本文为了避免漫无目的地选取NES 参数，建立了用于柱体结构涡激振动抑制的NES 减振装置优化设计仿真模型，使用优化算法快速设计出合适的NES 来有效抑制柱体结构的涡激振动，为实物设计提供参考设计目标。

1 柱体VIV 响应预测模型

物理模型如图1 所示：图1(a)中为二维平面内包含NES 的单自由度柱体模型，把柱体结构看成质量-弹簧-尼系统，嵌入的NES 也同样看作质量块，和柱体横向上有阻尼器和立方非线性弹簧连接；图1(b)为三维柱体涡激振动模型，来流经过柱体后，对柱体横向上产生振动。

根据该物理模型可得到NES 作用下单自由度柱体运动的控制方程[18]为：

图1 物理模型示意图Fig. 1 Physical model

2 优化方法

使用优化算法与VIV 仿真模型相结合，以NES对柱体涡激振动的抑制要求作为优化目标，对NES 参数进行优化设计，建立NES 减振装置优化设计仿真模型。

2.1 优化条件

优化模块中，以NES 的三个参数(无量纲质量之比 β、无量纲阻尼之比 ξ和无量纲刚度之比γ)为设计参数。这三个参数是设计NES 的重要参数，它们决定了NES 对柱体涡激振动的抑制效果，也是优化过程中的设计变量。

涡激共振的发生，结构横向上将产生大幅度的振动，受到周期性的疲劳应力作用，从而可能导致钝体结构的疲劳失效，甚至造成对结构的破坏。若结构长期处于频率锁定状态，将大大减少结构的疲劳寿命。为了减小涡激振动对柱体结构的疲劳损伤，通常设计减振装置以限制设计来流速度范围内的最大振幅。本文将VIV 预测模型计算出的设计工况下柱体稳定振动时的最大横向振幅为优化目标函数，使柱体横向振幅在一定折减速度内产生的最大值控制在最小值(即设定风速段内各振幅值均方差最小)，达到限制涡激振动的目的。

2.2 优化流程

优化流程主要是基于柱体VIV 模型对一定设计参数下的柱体振动响应进行模拟，在此基础上优化模块对设计参数进行优化使柱体振动响应接近目标条件，最后判断NES 对柱体涡激振动的抑制效果是否满足输出条件。满足后输出设计参数，若不满足则将优化后的设计参数再代入第一步循环，直到输出满足条件的NES 参数。优化流程如图2 所示。

图2 优化流程图Fig. 2 Optimized flow chart

2.3 优化算法

本文采用遗传算法完成对设计参数的优化。遗传算法[21]是一种模拟自然进化过程寻找最优解的方法。20 世纪70 年代，遗传算法由密切根大学Holland[22−23]最先开始研究，并运用于模拟生物学的进化过程。之后，由Bagley[24]正式提出“遗传算法”一词，并发表出世界上第一篇关于遗传算法应用的论文。遗传算法通过对变量进行编码，能将实际问题转化为对编好代码进行的处理，方便解决了变量的离散性问题。遗传算法使用目标函数本身建立优化方向，不需要大量的求导求逆等运算，也能为优化结果设置约束条件，因此常常被用来求解多目标的无功优化问题。本文将遗传算法与能快速计算出结果的经验模型相结合，建立了一个NES 减振装置优化设计模型，运用遗传算法对设计参数进行全局寻优，找到最接近优化目标满足条件的NES 参数。

遗传算法模型的主要求解步骤如下：

1)对NES 参数进行编码；

2)初始化种群，确定起始搜索点的初始种群数据；

3)根据优化目标振幅建立适应度函数，以适应度的大小判定个体的优劣，振幅越小，个体越优，遗传机率越大(求解适应度函数即求解VIV 预测模型)；

4)对种群进行选择，交叉，变异操作，以迭代生成下一代遗传群体；

5)判断遗传群体是否满足收敛条件和约束条件，若满足则结束运算，得出最优解；否则重复第4)步。

3 计算结果及分析

3.1 VIV 模型验证

为了验证Van der Pol 尾流振子模型能够以一定的精度预测柱体的涡激振动响应，本文使用与Stappenbelt 等[25]实验中相同的实验参数，计算得到无NES 作用下的圆柱振动响应，对比实验数据验证模型。取文献中两组参数作为Van der Pol 尾流振子模型的验证工况：第一组柱体直径D=0.0554 m，柱体阻尼比 ς=0.0056 ，圆频率ω0=7.486 rad/s，质量比m∗=6.54 ；第二组柱体直径D=0.0554 m，柱体阻尼比 ς=0.0057 ，圆频率ω0=6.0276 rad/s，质量比m∗=10.63。

本文模型与Stappenbelt 实验数据和CFD 计算结果对比如图3 所示。图3(a)为不同折减速度下柱体的振幅分布，从图中可看出，高质量比情况下，模型模拟结果在下端分支表现出与实验结果更为贴合。Van der Pol 尾流振子模型与实验结果有一致的变化趋势，所以Van der Pol 尾流振子模型可以一定程度上模拟出柱体的涡激振动。但由于经验公式的限制性，当Ur在3～6 时，模型与实验和CFD 数据都有一些差距。Van der Pol 尾流振子模型中有较少的经验参数，仿真的结果取决于经验参数的选取。如果经验参数并不是十分适用于该工况，就会与实验结果产生较大的偏差，而通常又无法给一个非常准又普适的经验参数。Dai 等[16]同样采用Van der Pol 尾流振子模型仿真柱体VIV，观察得到：该模型在频率锁定区间，基本上能捕捉到最大振幅。图3(b)为频率比随约化速度变化图，从图中可以观察到频率“锁定”现象。当Ur在4～8 时，柱体的振动频率与固有频率之比接近于1，同时对应于图3(a)，振幅在Ur=4 ～8时也显著大于其他折减速度下。

图3 基于Van der Pol 尾流振子模型的VIV 计算结果Fig. 3 The VIV simulation results based on Van der Pol wake oscillator model

文中CFD 方法计算柱体涡激振动不仅需要使用动网格，而且建立VIV 响应预测模型困难。在本人的前期工作文献[26]中已建立柱体结构的涡激振动高保真仿真模型。从图3(a)中可看出，基于CFD 和嵌套网格技术的涡激振动模型具有更高的仿真精度，但是计算效率远远小于Van der Pol尾流振子模型，不适用于与优化算法结合进行设计。文献[26]中同样的单核CPU 计算条件下，采用建立的CFD 二维弹性支撑柱体涡激振动仿真系统计算一个工况需要20 h 左右，而采用Van der Pol尾流振子模型仅需要10 s 左右的时间。因此，用于描述涡激升力的Van der Pol 尾流振子模型计算效率高，也基本可以捕捉到柱体的涡激振动特性，可应用于本文中建立NES 优化模型。

3.2 优化结果及分析

对该NES 作用下的柱体涡激振动情况进行验证，在该NES 作用下，设计折减速度内的计算结果如图4 所示。图4(a)为最大振幅随折减速度变化曲线图，从图中可看出，无NES 情况下，折减速度Ur=5.5时，振幅接近0.5 并达到最大值。NES作用情况下，在折减速度Ur=3 ～4.5和Ur=6.5 ～7时，振幅都几乎为0；而在折减速度Ur=4.5 ～6.5区间，柱体横向振幅显著增加，并在Ur=6时，振幅达到最大值。在折减速度Ur=6时，柱体产生最大振幅，但此时y1max/D依然在0.2 以内，说明在该折减速度范围内柱体的涡激振动振幅都较小，满足设计减振要求。其中增加了文献[15]中NES参数下的振幅随折减速度变化曲线， β=0.05、ξ=0.8 、 γ=0.8，文中发现在这几个参数下NES对涡激振动的抑制效果良好，故用于文中进行对比。从图中可看到，该NES 作用下柱体振幅略小于无NES 情况下，可见减振效果尚未达到目标。图4(b)为频率比随折减速度变化曲线对比图。从图中可以看出，单个柱体在折减速度Ur=4.5 ～5.5时，发生了频率锁定现象，对应于图4(a)中振幅也达到较大值；而加了NES 以后，频率比在Ur=4.5 ～5.5这一区间依旧继续上升，避免了涡激共振的产生，以此达到减振效果。由此可知，通过本方法设计完成的NES 对柱体涡激振动具有良好的抑制作用，可根据本模型设计方法应用于柱体减振装置设计。

观察到优化NES 与文献[15]中NES 主要是β的变化，所以同样将文献[15]中NES 的 β修改为0.1 和0.15 进行对比，得到如图4(c)所示的最大振幅随折减速度变化曲线图。从图中可以看出，随着 β的增大，NES 对柱体涡激振动的抑制效果更好。优化NES 的效果要优于文献[15]中NES β=0.15 的情况，同时 β也小于0.15，证明了本文建立优化模型的可用性。

图4 设计速度下的计算结果Fig. 4 Calculation results at design speed

柱体有无NES 作用的振动响应对比如图5 所示。图5(a)为振动位移对比图，振幅小的曲线为在设计NES 作用下柱体产生最大振幅来流速度下Ur=6的振动位移，振幅大的曲线则是单个柱体产生最大振幅来流速度下Ur=5.5的涡激振动位移图。从图中可以看出，无NES 情况下的柱体最大无量纲振幅将达到0.5，远大于NES 作用情况下，说明在该折减速度范围内下柱体的涡激振动都得到了较好的抑制，满足了设计要求。图5(b)则是对应于图5(a)中振动位移曲线的功率密度谱，从图中可以看出，无NES 情况下频谱曲线在2 Hz 处到达峰值，对应于柱体的固有频率处，代表在该折减速度下正发生着涡激共振；红线为NES 作用情况下，频谱曲线产生了更多的波动，但频谱曲线峰值避开了柱体固有频率2 Hz，避免了频率锁定的发生，这也是NES 能抑制涡激共振的主要原因。

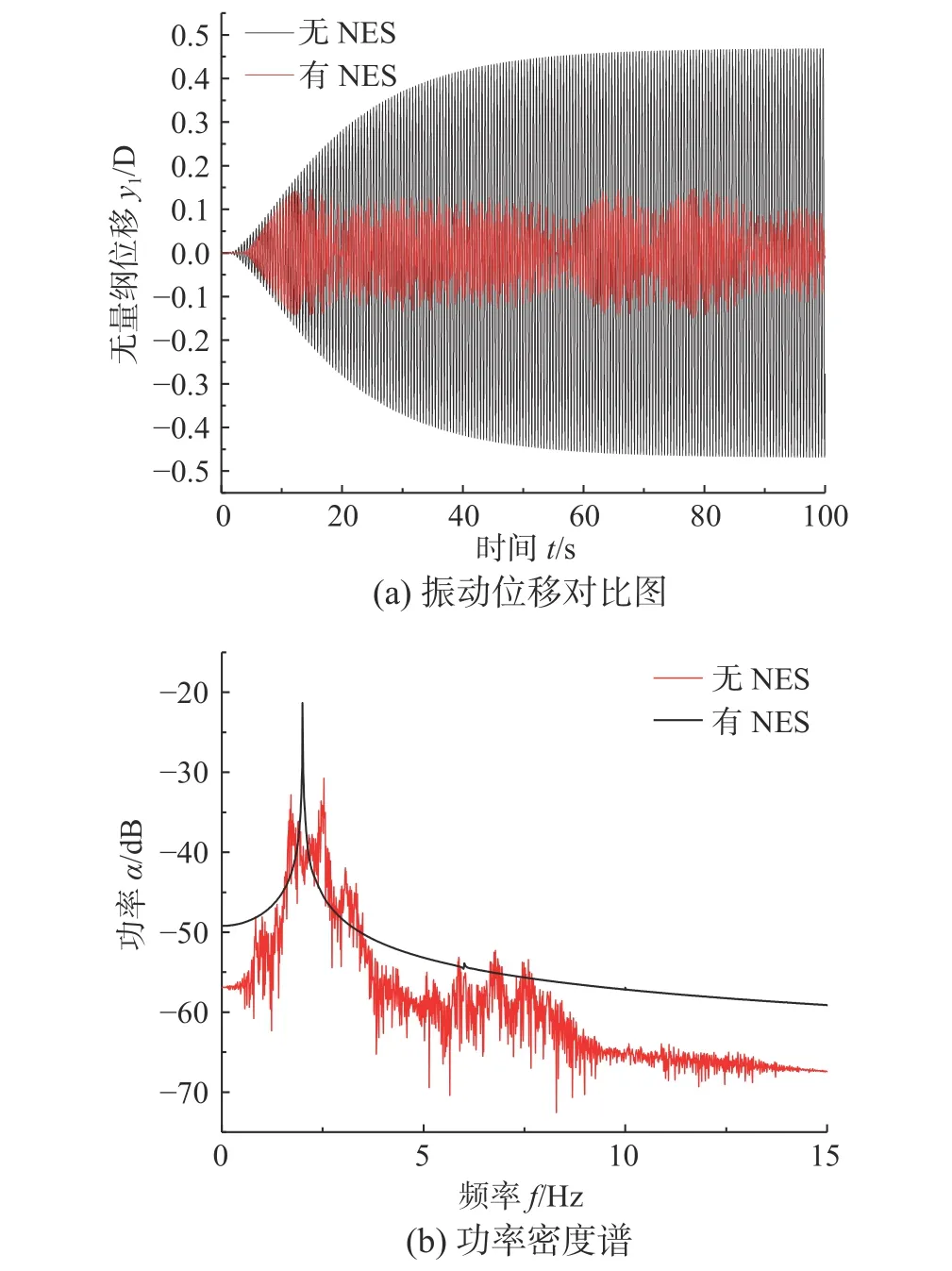
图5 振动响应对比图Fig. 5 Comparisons of vibration response

当Ur=5.5时，柱体有无NES 情况下涡激振动二维相图如图6 所示，图中横坐标为柱体的横向位移，纵坐标为柱体横向振动速度，外部曲线为无NES 情况下的柱体振动相图，内部曲线为NES 作用下柱体振动相图。可以从图中看出，无NES 情况下的曲线相轨被限制在极限环上，此时柱体发生等幅振动；而NES 作用下的相轨则在一定范围内波动，说明在NES 作用下柱体横向振动变得不规律，但NES 作用下的曲线最大半径远小于另一条曲线，说明此时NES 对柱体振动起到了限制作用。

图6 柱体涡激振动二维相图Fig. 6 Two-dimensional phase diagram of VIV of the cylinder

4 结论

本文基于Van der Pol 尾流振子模型、结构动力学和遗传算法，引入NES 被动控制装置，建立了用于抑制柱体结构涡激振动的NES 减振装置优化设计仿真模型。应用本方法针对一实例进行验证，对比分析了优化设计前后的柱体的振动响应结果，并研究了NES 的减振机理。

(1)用于描述涡激升力的Van der Pol 尾流振子模型，相较于计算流体力学方法，计算效率高，可以用于快速捕捉到柱体的涡激振动特性。由于其高计算效率，使之能与遗传算法相结合，建立了以模型预测结果为优化函数的高效优化模型。

(2)优化后的NES 能使柱体振动错开频率锁定区域，避免产生涡激共振，从而有效抑制柱体横向振动。在Ur=5.5时候，NES 作用下的柱体振幅最大减小了66.39%，减振效果明显。

(3)不可压缩定常流动下，柱体涡激振动通常为等幅振动；而NES 有效抑制柱体振动情况下，柱体往往在一定振幅范围内不规则振动，振动频率避开频率锁定区间。