功能梯度梁静力与动力分析的格林函数法

邓先琪，苏 成,2，马海涛

(1. 华南理工大学土木与交通学院，广州 510640；2. 华南理工大学亚热带建筑科学国家重点实验室，广州 510640；3. 广州大学工程抗震研究中心，广州 510405)

功能梯度材料(Functionally graded material)[1]指由两种或两种以上不同材料复合而成，且各组成成分的结构和性能在空间上沿着某一方向呈连续梯度变化的一种新型非匀质复合材料。由于其新颖的材料可设计性思想和优良的结构性能，近年来引起学者的广泛关注和研究[2−5]。文献[6 − 8]对功能梯度材料的力学性能与研究进展进行了综述。

目前，关于材料性能沿梁高度方向梯度变化的功能梯度梁静动态响应分析问题，解析方法和数值方法已有大量的研究。Sankar[9]假定材料弹性模量沿梁高度方向按指数函数变化，采用Euler-Bernoulli 梁理论给出了功能梯度简支梁在正弦分布荷载作用下的弹性力学解；而Zhong 和Yu[10]则基于Airy 应力函数给出了功能梯度悬臂梁的二维弹性力学解。Li[11]提出了功能梯度Timoshenko 梁和Euler-Bernoulli 梁的静力与动力分析统一列式。Simsek[12]利用不同的高阶梁理论分析了功能梯度梁的基本频率。Chakraborty 等[13]基于一阶剪切变形理论提出了一种新的梁单元来研究功能梯度梁的静力、自由振动和波动力学行为；而Kadoli 等[14]则基于高阶剪切变形理论，提出了高阶梁单元来进行功能梯度梁的静力分析。Filippi 等[15]基于一类统一列式提出了一种功能梯度梁单元模型，并对功能梯度梁静力问题做了相关的研究。Pradhan和Murmu[16]采用微分求积法研究了材料参数沿高度方向呈幂函数形式分布的弹性地基功能梯度梁和层合梁的振动问题。Jiao 等[17]基于一阶剪切变形与经典梁理论，采用微分求积法分析了功能梯度梁的线性弯曲问题。李世荣和刘平[18]基于Euler-Bernoulli 梁理论，比较了功能梯度梁和均匀梁的控制微分方程，得到了功能梯度梁与均匀梁静动态解之间的相似转换关系。王瑄和李世荣[19]基于Levinson 高阶剪切变形理论，研究了两端简支功能梯度梁自由振动频率与经典梁理论下参考匀质梁自由振动频率之间的解析转换关系。以上文献中仅考虑了材料沿梁高度梯度变化的情况。

相比于材料性能沿梁高度方向梯度变化的功能梯度梁，关于轴向功能梯度梁静力与动力分析的研究相对较少。轴向功能梯度梁的控制微分方程本质上是一个变系数常微分方程，通常情况下很难获得该类方程的解析解。在数值方法方面，Murín 和Kutiš[20]采用传递系数描述功能梯度梁在空间上变化的弹性模量，建立了功能梯度Euler-Bernoulli 梁的等效刚度矩阵。Alshorbagy 等[21]提出了材料沿轴向或高度方向梯度变化的功能梯度梁动力特性分析的有限元法。汪亚运等[22]基于切比雪夫多项式展开技术研究了轴向功能梯度变截面梁的自由振动问题。

本文主要研究弹性模量沿轴向梯度变化的功能梯度Euler-Bernoulli 等截面梁的静力与动力分析问题。由于这种梁的弹性模量沿轴向呈函数变化，因此采用传统有限元法进行结构分析时，不可避免地要进行有限单元网格细分，随之带来的问题是计算规模的增大与计算效率的降低。为了提高功能梯度梁静动力问题的计算精度与效率，本文首先将功能梯度梁静力分析的控制微分方程转化为与匀质材料等截面梁静力分析控制微分方程相一致的形式，然后利用无限长匀质材料等截面梁静力问题的格林函数[23]，提出了功能梯度梁静力分析的格林函数法。在此基础上，进一步推导获得功能梯度梁的柔度矩阵，据此建立功能梯度梁的运动方程，开展功能梯度梁的动力特性分析和动力响应分析。

1 功能梯度梁静力分析

1.1 基本方程

考虑弹性模量沿轴向梯度变化的功能梯度梁静力分析的控制微分方程为：

式中：x为梁的轴向坐标；u(x)和v(x)分别为梁的轴向位移和横向位移；E为参考匀质梁的弹性模量； η(x) 为反映弹性模量沿轴向变化的函数；A和I分别为梁的截面面积和截面惯性矩；p(x)和q(x)分别为梁的轴向和横向分布荷载。

根据微分运算关系，式(1)可以转化为：式中，F1(x)和F2(x)分别为梁的等效分布荷载，表示为：

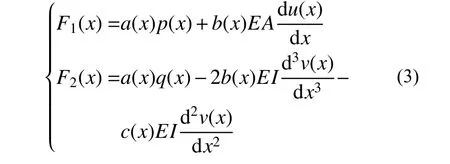
式中：

由式(2)可以看出，功能梯度梁静力分析的控制微分方程可以写成与匀质梁静力分析的控制微分方程相似的形式，唯一的差别在于式(2)中的等效分布荷载与方程左端梁的位移相关联。尽管如此，仍可以利用匀质梁静力问题的格林函数[23]进行求解。

利用匀质梁静力问题的格林函数进行求解时，在内力计算上存在一些不同。考虑到材料的非匀质性，功能梯度梁内力与位移之间的微分关系为：

式中，b(x)见式(4)。

由式(5)可见，在功能梯度梁的静力分析中，内力与位移微分关系在形式上与匀质梁问题的内力与位移微分关系并不完全一致。因此，在采用匀质梁静力问题的格林函数进行求解时，需要考虑函数 η(x) 及修正项b(x)M(x)对内力的影响。

利用式(5)，可将式(3)给出的等效荷载表示为：

由式(6)可见，等效荷载可以写成与内力N(x)、Q(x)和M(x)相关的形式，因此在采用格林函数法分析时，需要建立关于内力响应的补充方程，方可求解。

1.2 静力响应分析算法

利用功能梯度梁静力分析控制微分方程和匀质梁静力分析控制微分方程在形式上的相似性，可以将功能梯度梁转化为如图1 所示的等效匀质梁ab 进行求解。其中，x−y为梁的坐标系，梁端点轴向坐标为xa和xb，弹性模量取为参考匀质梁的弹性模量E，截面面积和截面惯性矩分别取为功能梯度梁的截面面积A和截面惯性矩I，轴向和横向分布荷载分别取为式(6)所示的等效分布荷载F1(x)和F2(x)。

图1 与功能梯度梁等效的匀质梁Fig. 1 A uniform beam equivalently to the functionally graded beam

采用域外虚荷载方法[24]，将等效匀质梁ab 嵌入到具有相同材料性质与截面性质的无限长梁中，并在梁ab 域外 ξj(j=1,2)处布设6 个大小未知的集中虚荷载Xij(i=1,2,3;j=1,2)。根据叠加原理，在域内等效荷载Fi(x)(i=1,2)与域外虚荷载Xij(i=1,2,3;j=1, 2)的共同作用下，梁ab 上任意一点的位移与内力响应为

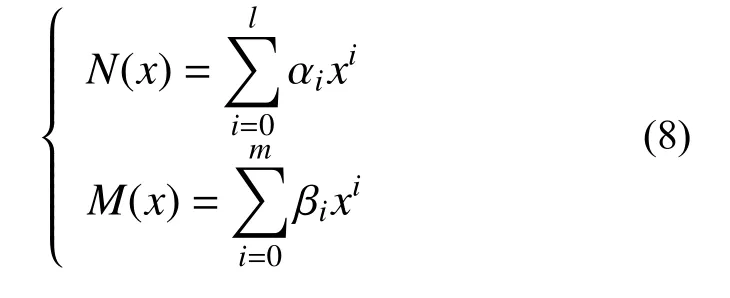
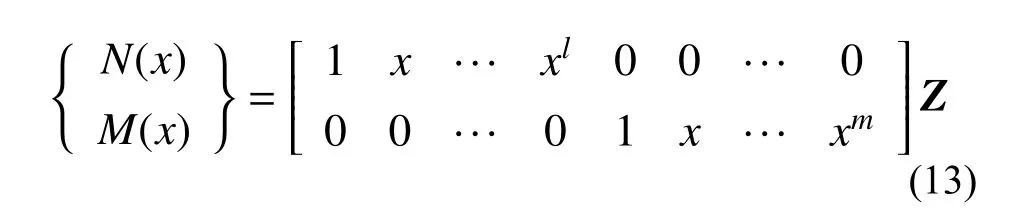
理论上，此式与式(10)在同一点处应给出相同的内力值。基于此，在梁域内选择(l+1)个点，利用轴力N(x) 相等可以得到(l+1)个方程；类似的，在梁域内选择(m+1 )个点，利用弯矩M(x)相等可以得到(m+1)个方程。最终可得：

式中，H的各行取决于式(13)系数矩阵在所选择点处的取值，而A˜ 、B˜ 和C˜的各行取决于式(10)中对应影响矩阵在所选择点处的取值。

联立式(12)和式(14)，可以解得：

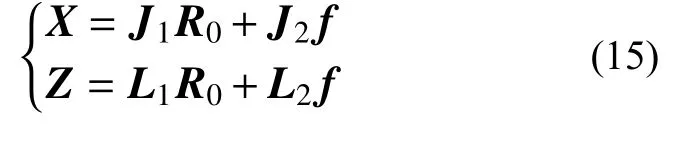
式中：

式中，I为 6×6的单位矩阵。

从以上推导可见，由式(15)求得的基本未知向量X和Z分别包含6 个虚荷载和(l+m+2)个内力系数，基本未知量数目与梁的子段划分无关，即与子段数n无关。

将X和Z代入式(10)，即可得到功能梯度梁内任意一点的位移和内力响应为：

式中：

2 功能梯度梁动力分析

2.1 柔度矩阵

令R0=0，由式(17)可以得到由子段荷载向量f引起的梁各子段中点xk(k=1,2,···,n)处的位移为：

式中，w=[u(x1)v(x1)u(x2)v(x2) ···u(xn)v(xn)]T，f见 式(11)， δ 可 由 δ2(x) 前 两 行 元 素 在xk(k=1, 2,···,n) 即 为 功能 梯 度 梁 对应 于w和f的 柔 度矩阵。

2.2 运动方程

阻尼矩阵可采用Rayleigh 阻尼模型生成。

2.3 动力特性和动力响应分析

式(21)可以退化为功能梯度梁无阻尼自由振动方程。利用传统的特征值问题求解方法，可以获得功能梯度梁的自振频率和振型。

在动力荷载f(t)的作用下，采用传统的振型分解法或直接积分法求解式(21)，可以获得功能梯度梁的位移响应w(t) 、速度响应w˙(t)和加速度响应w¨(t)。同时，考虑外荷载、惯性力和阻尼力的作用，由式(17)可以进一步获得功能梯度梁内任意一点处的位移和内力响应为：

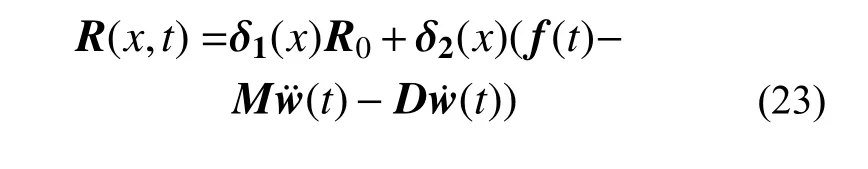
3 数值算例

本文所采用的格林函数法和有限元法计算程序均采用Python 编程语言进行编写，并在桌面电脑(Intel®Core™i7-2620 CPU, 8-GB RAM)上运行。

3.1 静力响应分析

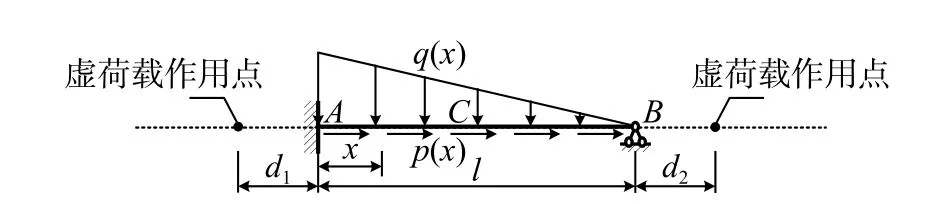
图2 一端固支、一端简支功能梯度梁Fi g. 2 A clamped-simply supported functionally graded beam

分别采用解析法、格林函数法和有限元法计算功能梯度梁的位移和内力。根据材料力学理论，该功能梯度梁的轴向与横向位移、轴力与弯矩解析解表达式分别为：

在格林函数法中，采用分段矩形积分公式计算式(7)中的域内积分项，分别取n=4 、 10 、 20、50 和 100以考虑子段数对计算精度的影响。在轴向和横向三角形分布荷载作用下，梁的轴力和弯矩分别为关于x的2 次和3 次多项式，因此分别将式(8)中的轴力和弯矩表示为相应次数的多项式，即l=2，m=3 ，并在梁内均匀选取(l+1 )和(m+1)个点分别建立关于轴力和弯矩的补充方程。将两端虚荷载施加位置与梁左右端点的距离表示为d1和d2，分别考虑d1=d2=0.2 m、d1=d2=0.4 m和d1=0.2 m及d2=0.4 m三种情况对格林函数法计算结果的影响。

在有限元法中，将功能梯度梁离散成Ne个基于Hermite 插值的平面二节点梁单元，分别取Ne=4 、 10 、 20 、 50 和 100以 考 虑 离 散 单 元 数 对计算精度的影响，其中每个梁单元的弹性模量取为梁单元中点处的弹性模量值。

表1 给出了功能梯度梁跨中点C 的轴向位移和横向位移结果，其收敛情况如图3 所示。表2给出了功能梯度梁固定端点A 的轴力和弯矩结果，其收敛情况如图4 所示。由上述图表可见，当子段数n≥20时，格林函数法的计算结果与解析解高度吻合，说明所提出方法具有理想的计算精度。此外，由计算结果还可以看出，虚荷载位置的三种选择对格林函数法计算结果没有任何影响，说明所提出方法具有良好的数值稳定性。

表1 功能梯度梁跨中点C 的轴向与横向位移Table 1 Axial and transverse displacement of node C at midspan of the functionally graded beam

图3 功能梯度梁跨中点C 的轴向与横向位移Fig. 3 Axial and transverse displacement of node C at midspan of the functionally graded beam

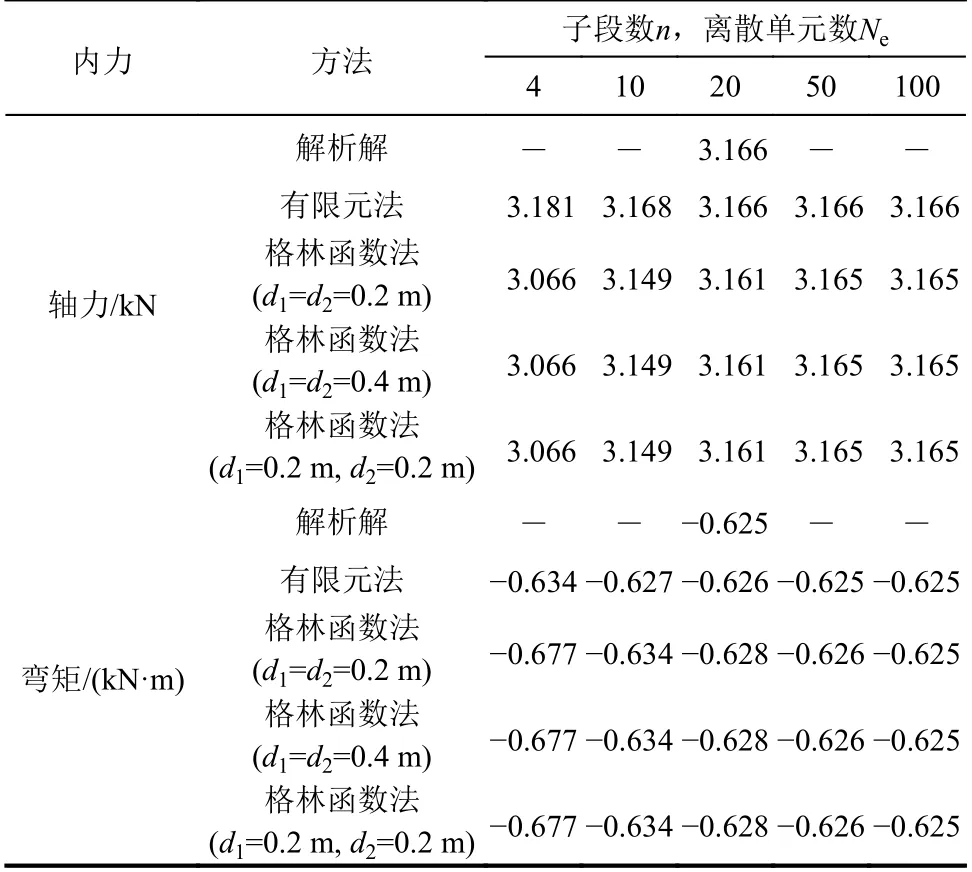
表2 功能梯度梁固定端点A 的轴力与弯矩Table 2 Axial force and bending moment of node A at fixed end of the functionally graded beam

图4 功能梯度梁固定端点A 的轴力和弯矩Fig. 4 Axial force and bending moment of node A at fixed end of the functionally graded beam

在计算效率方面，格林函数法中的基本未知量为虚荷载X和内力系数Z，详见式(12)和式(14)，未知量数目并不受子段数n的影响，因此即使n取较大值也不会影响方程组的求解效率。而在有限元法中，随着离散单元数Ne的增加，基本未知量数目和刚度矩阵规模也相应增多，从而计算工作量也会显著增加，计算时间延长。

3.2 动力特性分析

考虑图2 所示一端固支、另一端简支的功能梯度梁。梁的截面面积、截面惯性矩和长度与算例3.1 中相应参数相同。假设梁的弹性模量和密度均沿轴向呈3 次多项式函数形式变化，表达式为：

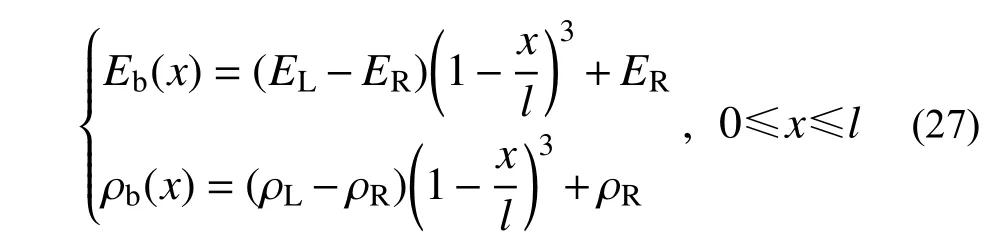
式 中：EL=210 GPa和ER=390 GPa分 别 表 示 梁左、右两端处弹性模量的取值；ρL=7800 kg/m3和ρR=3960 kg/m3分别表示梁左、右两端处密度的取值。

分别采用格林函数法和有限元法计算功能梯度梁的自振频率。在格林函数法中，反映虚荷载位置的距离取为d1=d2=0.2 m。为了考察子段数n对计算精度的影响，分别取n=10 、 20 、 30、40 、 50 和 200。由于梁在自由振动过程中其内力分布不再满足简单的多项式分布形式，为了考察弯矩多项式次数m对横向自由振动固有频率的影响，分别取m=4、6、8 和10，而轴力多项式次数则取为l=10。在有限元法中，将功能梯度梁离散成Ne个基于Hermite 插值的平面二节点梁单元，采用一致质量矩阵。分别取Ne=10 、 20、30 、 40 、 50 和 200 以考察离散单元数Ne对计算精度的影响，其中每个梁单元的弹性模量取为梁单元中点处的弹性模量值。

表3 和图5 给出了功能梯度梁的前三阶横向自由振动固有频率的计算结果。由计算结果可见，当m>6 时，在子段数n和离散单元数Ne取为相同的情况下，格林函数法计算得到的前三阶横向自由振动固有频率总是比有限元法计算得到的结果精度更高，收敛速度更快。也就是说，当弯矩多项式次数足以反映真实弯矩分布时，要达到相同的精度，格林函数法所需要的子段数n少于有限元法所需要的离散单元数Ne，因此其计算效率更高。

表3 功能梯度梁前三阶横向自由振动固有频率Table 3 The first three natural frequencies of functionally graded beam’s transverse free vibration

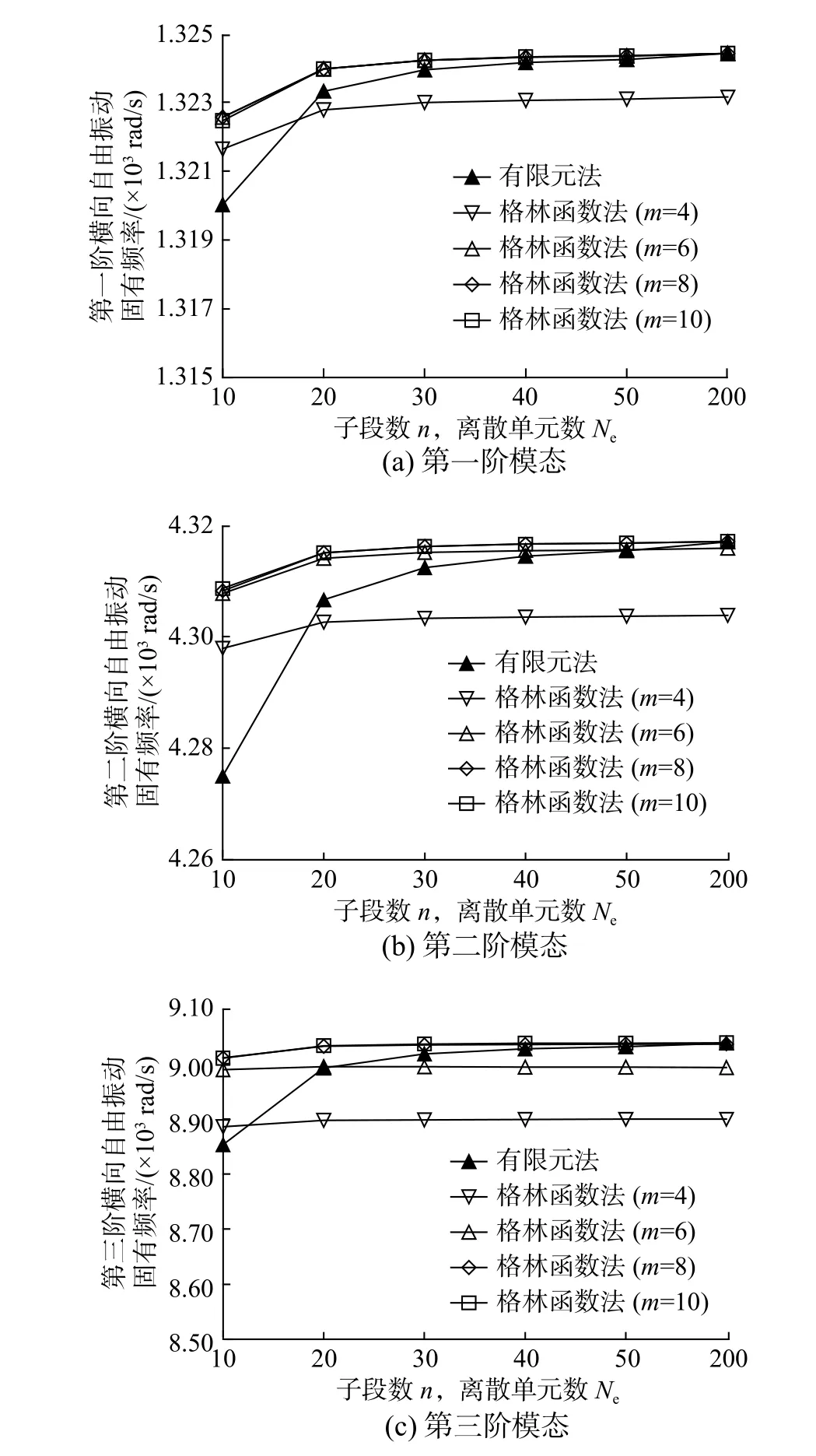
图5 功能梯度梁前三阶横向自由振动固有频率Fig. 5 The first three natural frequencies of functionally graded beam’s transverse free vibration

3.3 动力响应分析

考虑图2 所示一端固支、另一端简支的功能梯度梁，其几何参数和材料参数与算例3.2 中的相应参数相同。梁受横向均布突加荷载q(t)作用，荷载随时间变化曲线如图6 所示。选取Rayleigh 阻尼模型，阻尼比取为 ζ=0.05(对应的自振频率ω1=1324.42 rad/s和ω2=4317.06 rad/s)。

图6 荷载-时间曲线Fig. 6 Load-time curve

分别采用格林函数法和有限元法计算功能梯度梁的位移、速度和加速度。在格林函数法中，反映虚荷载位置的距离取为d1=d2=0.2 m，内力多项式次数取为l=m=8 。为了考察子段数n对计算精度的影响，分别取n=10 、 20 和 30。在有限元法中，将功能梯度梁离散成Ne个基于Hermite插值的平面二节点梁单元，采用一致质量矩阵。取Ne=200以获得相对精确解，其中每个梁单元的弹性模量取为梁单元中点处的弹性模量值。两种方法均采用Newmark- β积分格式求解运动方程，积分步长均取为 ∆t=1.0×10−4s ，共计算 500个时间步。

图7 给出了功能梯度梁跨中点C 的横向位移、速度和加速度结果，上述结果在0.03 s 后的时间内基本不再变化。从图中可见，当子段数n=30时，格林函数法计算得到的跨中点C 的横向位移、速度和加速度响应与有限元法结果高度吻合，再次说明所提出方法具有理想的计算精度。

图7 功能梯度梁跨中点C 横向位移、速度和加速度Fig. 7 Transverse displacement, velocity, acceleration of node C at midspan of the functionally graded beam

4 结论

本文提出了一种轴向功能梯度材料Euler-Bernoulli 梁静力与动力分析的格林函数法。将功能梯度梁静力分析的控制微分方程转化为与匀质材料梁静力分析控制微分方程相一致的形式，从而可以利用匀质材料梁静力问题的格林函数进行求解。在此基础上，进一步可以推导得到功能梯度梁的柔度矩阵，并建立功能梯度梁的运动方程，开展功能梯度梁动力特性分析与动力响应分析。数值算例表明，对于功能梯度梁的静力和动力问题，格林函数法比有限元法具有更高的计算精度和计算效率。