交换p群的整群环以及它的极大序的K1群*
2020-09-17 01:20杨全李唐国平
中国科学院大学学报 2020年5期
杨全李,唐国平
(中国科学院大学数学科学学院, 北京 100049)

1 预备知识
定义 1.1对阶为素数p的幂的交换群G,由有限生成交换群的结构定理可将G唯一地表示为某些pki阶循环群的直和,i=1,2,…,n,且k1≤k2≤…≤kn,数组(k1,k2,…,kn)p称为群G的型。
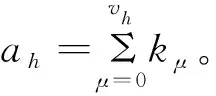
证明见文献[1-3]。
引理 1.2对代数数域F的代数整数环OF,有SK1(OF)=1。
证明见文献[4]。

证明见文献[5]。

证明见文献[6]。

证明见文献[7]。

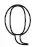
0→D(Λ)→CL(Λ)→CL(Γ)→0.

引理 1.6有正合序列


且有
(i)

(ii)

其中Jp0是Γp0的Jacobson根。
证明见文献[10]。



且

其中t=t(G)=m-1是G的非平凡循环子群的个数。
证明见文献[10]。

证明见文献[11]。
2 主要结果
定理 2.1若G=Cpn,(n≥0),则




从而
于是由引理1.7得


当n=0时,上式显然成立。
定理 2.2当G=Cpn×Cpn,(0≤n)时,则

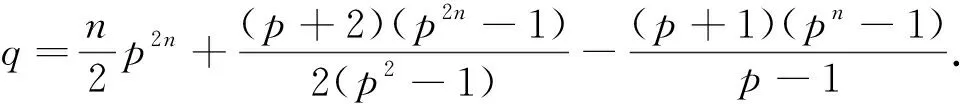

=(p+1)ph-1.
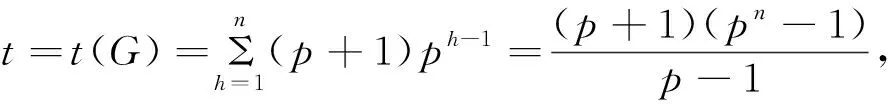


根据文献[12]有关分圆域的判别式的计算公式

于是在这种情形下有
由引理1.7得

=p2q,

上式对n=0情形显然成立。
定理2.3当G=Cpn1×Cpn2,0 其中 =(p+1)ph-1. =pn1. 综上所得有 于是 由引理1.7 =p2q. 综合定理2.1~定理2.3的结果有 定理 2.4对G=Cpn1×Cpn2,0≤n1≤n2,有 其中 对于任意(k1,k2,…,kn)p型的交换群,相应的计算公式非常难以给出,然而对下面特殊情形,有 定理 2.5当G=(Cpn)l,n≥0;l>0时有 其中 于是由引理1.7 =p2q, K1(Γ)=(Γ)×⊕SK1(Γ), =2. =24. =212. =1. =2. =24. =210. (i)由定理2.5可得 =24, (ii)由定理2.5可得 =211,
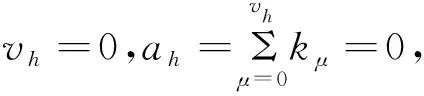
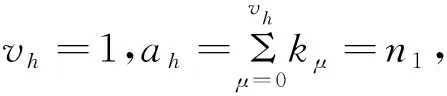




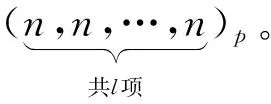
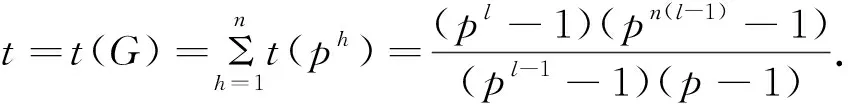












































猜你喜欢
防爆电机(2022年4期)2022-08-17
语数外学习·初中版(2022年4期)2022-06-10
南宁师范大学学报(自然科学版)(2021年1期)2021-04-27
中等数学(2020年7期)2020-11-26
新高考·高二数学(2017年8期)2018-03-13
高中生学习·高二版(2017年9期)2017-10-25
福建中学数学(2016年9期)2016-12-14
中学生数理化·中考版(2016年8期)2016-12-07
考试周刊(2016年44期)2016-06-21
新高考·高一物理(2014年4期)2014-09-17

