近临界压力区Post-dryout传热特性分析

宋美琪，刘晓晶，程 旭

(1.上海交通大学 核科学与工程学院，上海 200240；2.Institute of Applied Thermofluidics,Karlsruhe Institute of Technology,Karlsruhe 76131,Germany)

对于超临界冷却系统，其设计工况为超临界区，不会出现沸腾危机现象。但当系统从次临界升压到超临界区或从超临界区泄压到次临界区过程中，必须考虑次临界高压区流动传热问题。Hong等[1]进行了近临界压力区R134a的传热特性实验研究，实验结果表明，近临界压力区临界热流密度(CHF)随压力的增高而降低，因临界点CHF将趋于0，即使极低热流密度下也会发生沸腾临界现象，进入到临界热流密度后(Post-CHF)传热区。同时对于流动工况，通常根据沸腾临界点含气率的大小将沸腾临界现象分为过冷或低含气率工况下偏离泡核沸腾(DNB)和高含气率工况下干涸(DO，dryout)两种类型，相应的Post-CHF传热也分为Post-DNB和Post-dryout两种。

近几十年来，针对Post-dryout区传热特性已提出大量分析方法，主要分为经验公式、半理论模型和现象模型3种。对于本文所关注的近临界压力区，物性参数随压力的变化大，低压区液滴尺寸及其分布、相间传热等模型不再适用，因此需研究专门的传热模型。目前，国际上对近临界压力区Post-dryout传热分析相对较少。Swenson等[2]进行了20.6 MPa压力下临界后传热实验，并通过对单相对流公式中系数的简单修改得到新的传热公式。Groeneveld等[3]提出了充分发展膜态沸腾表，其中最高压力可达20 MPa，但因查表法的局限性，不能进行外推。Bishop等[4]和Groeneveld[5]提出了临界后传热关系式，压力范围分别为16.5～21.5 MPa和3.4～21.5 MPa。

为对现有模型方法进行评估，本文收集并整理近临界压力区水的Post-dryout传热数据，建立数据库，依据数据库开发新的传热关系式。

1 传热机理分析

假设Post-dryout区流型为弥散流，液相以液滴的形式存在，弥散在主流气相中。若忽略辐射换热的影响，存在3种主要传热机制：1) 壁面对主流气相的对流传热；2) 壁面对液滴的直接加热；3) 主流气相向液滴的传热。

假设液相处于饱和状态，因气液两相之间存在温度差，过热气相与饱和液相之间存在热量交换，系统处于热力学不平衡状态，因此气相温度和两相速度很难确定，尚无可靠的传热模型。

1.1 充分发展Post-dryout区的判断

假设系统处于完全热力学平衡状态，通过壁面传给蒸汽的热量全部用于液滴蒸发，蒸汽温度等于饱和温度而不发生过热，同时认为不存在壁面和液滴之间的直接传热，此时壁面与主流之间的传热Nusselt数可通过单相气体Dittus-Boelter公式(式(1))来预测，进而可由式(2)、(3)求得完全热力平衡假设下的壁面温度Tw，eq。实验所测壁面温度Tw，m与完全热力平衡假设下计算所得壁面温度Tw，eq的比较如图1所示，沸腾临界发生后，实验所测壁面温度是低于平衡壁面温度的，认为此时仍存在壁面与液滴间的对流换热，将此区域定义为未充分发展Post-dryout区，之后随壁面温度的继续升高，实验所测壁面温度开始高于平衡值，认为进入充分发展Post-dryout区。本文研究对象为充分发展Post-dryout区传热。

图1 实验所测壁面温度与平衡状态壁面温度的比较Fig.1 Comparison between measured and equilibrium wall temperatures

(1)

(2)

(3)

其中：Nu为Nusselt数；G为流道总质量流量；D为流道水力学直径；X为质量含气率；μV为气相动力黏性系数；α为空泡份额；PrV为以气相温度为定性温度的Prandtl数；αeq为完全热力平衡假设下的对流传热系数；λV为气相导热系数；q为加热壁面热流密度；TV为系统中的气相温度：

其中：TV，e为完全热力平衡假设下的气相温度；Ts为饱和温度；xe为平衡含气率。

1.2 Post-dryout区传热模型

由实验结果计算传热系数时，通常认为主流温度等于平衡状态下的气相温度，根据Nu定义和对流换热公式可得计算Nu的表达式为：

(4)

其中，Tw为加热壁面温度。

假设采用Dittus-Boelter公式计算Nu：

(5)

(6)

其中：CTP、nTP和mTP为常数；ReTP为两相Reynolds数；PrTP为两相Prandtl数。

同时假设两相流体导热系数、动力黏性系数及比热容等热力学参数可由相应的饱和液相和饱和气相值及平衡含气率给出：

λTP=xeλV+(1-xe)λL

(7)

其中：λTP为两相导热系数；λL为液相导热系数；μTP为两相动力黏性系数；μL为液相动力黏性系数。

所以两相Reynolds数ReTP和两相Prandtl数PrTP可分别表示为：

(8)

(9)

其中：cp，TP为两相比热容；cp,w、μw和λw为以壁面温度为定性温度的气相比热容、动力黏性系数和导热系数；fPr为Prandtl数的修正系数。

即两相Reynolds数ReTP和两相Prandtl数PrTP可分别表示为计算用物性参数(导热系数、动力黏性系数及比热容)与物性修正系数的乘积。因此NuTP可表示为：

NuTP=CTP(ReV·fRe)nTP(Prw·fPr)mTP

(10)

其中，fRe为Reynolds数的修正系数。

根据NuTP定义式可得到Nu与真实NuTP间的关系为：

(11)

将式(10)代入式(11)整理可得：

Nu=C·FTw·Fproperty·

(12)

2 传热模型建立和误差分析

2.1 Post-dryout区数据库简介

本文所选用的Post-dryout区数据库数据范围列于表1，实验点数目为3 151。数据取自Herkenrath等[8]、Bishop等[9]、Swenson等[2]及Becker等[10]的均匀加热竖直圆管内向上流动Post-dryout区实验，工作介质为水。最高工作压力接近临界点，达到21.5 MPa。表1中：p为压力；X为质量含气率；Ts为饱和温度。

表1 Post-dryout区数据库参数范围Table 1 Parameter range of Post-dryout region database

2.2 模型建立

根据式(12)，需首先确定由ReTP和Prw组成的参考公式，再确定相应的修正系数。由于nTP和mTP是未知的，这里选取单相对流换热公式形式的参考公式，nTP和mTP的初始值分别设为0.8和0.4，常数的初始值为0.023，即：

(13)

其中，Nu0为参考Nusselt数。

则Nu可表示为：

Nu=F·Nu0

(14)

其中，F为Nusselt数修正系数。

为构建修正系数关系式，需首先找出与其相关的关键参数。如图2所示，将3 151个数据点分别按照ReTP和Prw的值进行排序后分组，绘制每组修正系数的均值μ和分布范围(μ-σ,μ+σ)。图2中，αc和αm分别为传热系数的计算值和实验值。与图2相同，对壁面温度修正系数、物性修正系数及两相不平衡修正系数等相关的无量纲参数进行分析后发现，修正系数F随ReTP和Prw的变化最为明显，故认为修正系数的关系式仅与ReTP和Prw有关，最终得到Nu表达式为：

Nu=5.894 6×10-5·

(15)

修正后关系式的误差随ReTP和Prw的变化如图3所示。由图3可见，修正后关系式的误差分布随ReTP和Prw的变化可忽略。这表明壁面温度修正系数、物性修正系数及两相不平衡修正系数可由ReTP和Prw来表示，而不需其他无量纲参数的引入。

2.3 误差分析

定义误差参数εi表达式为：

(16)

平均误差μ和均方根误差RMSE公式分别为：

(17)

修正后的传热系数表达式(式(15))与实验数据相比，由式(17)计算可得平均误差为0.9%，均方根误差为14.4%。

图4示出误差参数εi随系统压力、质量流量、水力学直径、平衡含气率、热流密度、壁面过热度等的分布。由图4可见：平衡含气率大于1.0时，误差参数随平衡含气率增加有明显降低的趋势，可能因为该区域的数据点较少，在关系式拟合过程中所占的比重较小，因而导致该模型不能很好地刻画传热系数随平衡含气率的变化；除平衡含气率外，误差参数范围不受系统压力、质量流量、加热管水力学直径等其他宏观参数的影响。表2列出其他传热关系式对于本文数据库的预测精度，从平均误差和均方根误差来看，本文提出的传热关系式优于其他方法。

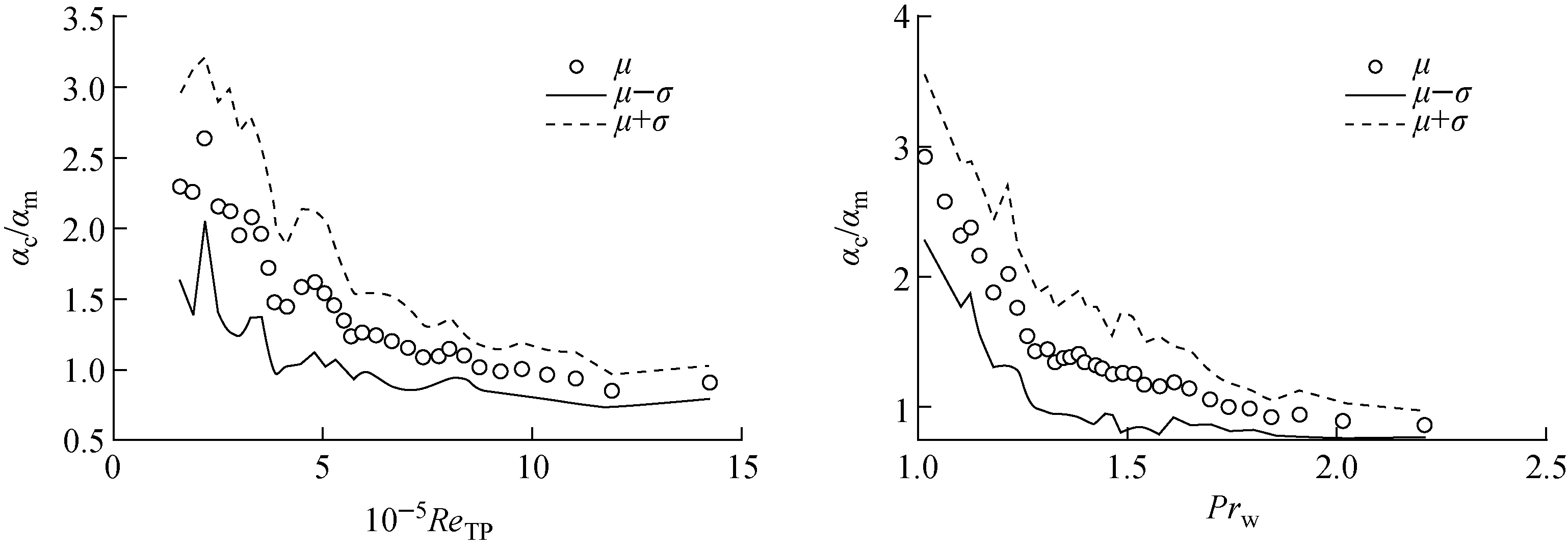
图2 参考关系式计算误差随ReTP和Prw的变化Fig.2 Variation of calculation error of reference formula with ReTP and Prw

图3 修正后公式误差随ReTP和Prw的变化Fig.3 Variation of calculation error of modified correlation with ReTP and Prw

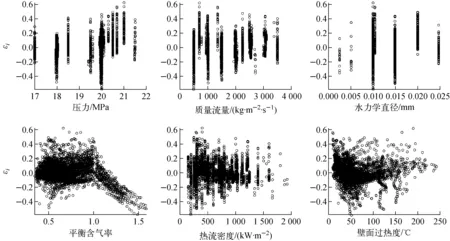
图4 误差参数随不同热工参数的变化Fig.4 Variation of error parameter with different hydraulic parameters

3 总结

本文通过对Post-dryout区传热机理进行分析，提出了一种新的充分发展Post-dryout区的判定准则，认为在充分发展Post-dryout区，不存在壁面对液滴的直接加热，仅有壁面对主流气相对流换热和主流气相向液滴的传热两种热量传递方式。对现有高压区(17 MPa以上)Post-dryout区数据库进行分析表明，两相Reynolds数和以壁面温度为定性温度的Prandtl数是与壁面温度、物性及两相不平衡性相关性最强的参数，基于此得到新的传热关系式。本文提出的传热关系式计算平均误差为0.9%，均方根误差为14.4%。与已有公式相比，新的传热关系式结构简单且预测精度更高。

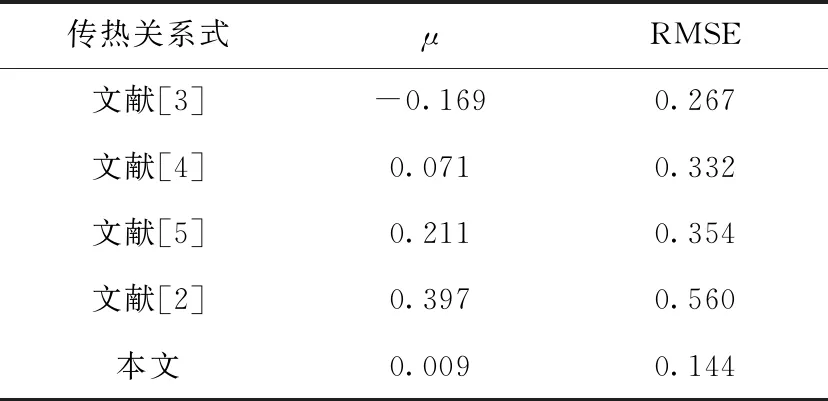
表2 传热关系式的误差Table 2 Error of heat transfer correlation