利用Z比分数分析试验间质量控制数据

曹文婷

(贵州省质安交通工程监控检测中心有限责任公司，贵州 贵阳 550000)

0 引 言

利用数理稳健统计法处理实验室给出的结果，并分析参加实验室的检测技术能力状况。采用Z比分数的结果来进行分析和判断。如显示结果异常，即判定其结果为不满意(或有问题)。

1 研究背景

本文基于某次作为发起实验室，组织的实验室间比对，对标志反光膜逆反射系数测定9对角的测试得出9个水平的分析数据，再通过Z比分数对实验室提交的数据进行分析，可以比较实验室之间的数据，强调实验室间的能力的差，是目前实验室间能力验证通用的统计方法。一般来说本统计技术能够较好地反映样品分析的总体状况。通过能力验证活动，参加实验室可以了解分析项目的整体水平和自已所处的位置，有利于找到差距，进一步分析原因，从而提高自身技术能力和管理水平。

2 统计概述

本主要对该次能力验证计划的稳健统计参数、参加实验室的总体能力状况、各参加实验室的能力比分数等进行了统计。统计稳健变异系数介于4.8%～10.3%之间，稳健变异系数是表示结果变异性的一个参数，由此可见参加该次能力验证实验室在9对角的整体分析水平较高。主要稳健参数的统计结果如表1所示。

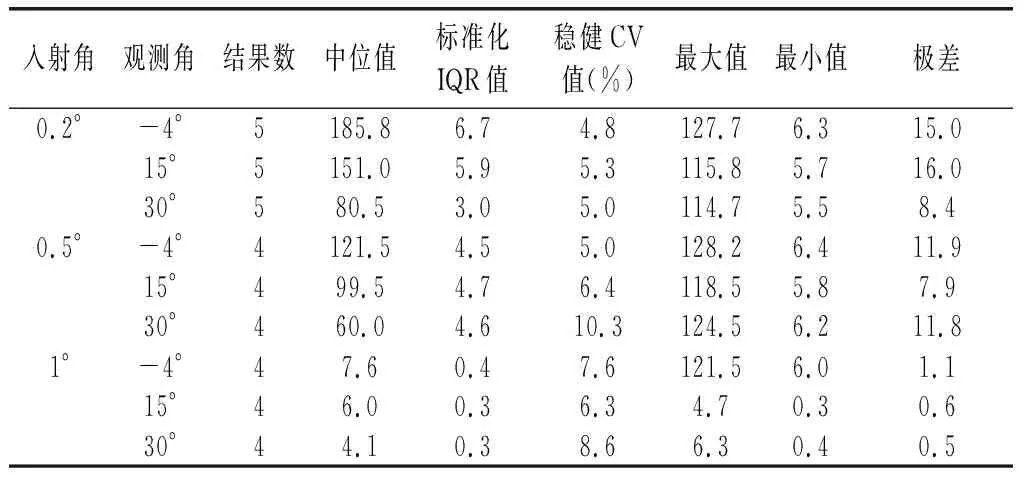
表1 主要稳健统计参数汇总表

3 格拉布斯离群检测

GB/T 4883-2008《数据统计处理和解释 正态样本离群值的判断和处理》中提到用样本中位值、标准差、最大最小观察值计算统计量Gn、Gn’，根据格拉布斯临界值判定样本的离群情况。

4 四分位稳健统计技术

该方法可以降低极端值(即离群值)对统计结果的影响，它对极端值的处理方式是尽可能降低其权重，而不是将其从数据组中完全剔除，使平均值估计值和标准差估计值被影响程度降至最小。该方法与经典统计方法相比在极端值的影响方面较为优越。其使用中位值、IQR值代替了传统的平均值、标准偏差，用稳健Z比分数代替经典Z比分数来评定参加能力验证的实验室的检测能力。

5 主要稳健统计参数

该次能力验证计划采用同一样品检测、四分位稳健统计技术，主要统计参数为：结果数量(N)、中位值(M)、标准四分位间距(NIQR)、上四分位值(Q3)、下四分位值(Q1)、稳健变异系数(CV)、最小值(MIN)、最大值(MAX)、极差(R)。其中最主要的统计参数是中位值和IQR，因为它们是稳健的统计量，较少受数据中存在的离群值的影响。各统计参数的数学含义与计算方法如下：

结果数量(N)：参加能力验证实验室按照作业指导书要求报告的有效检测结果数目。

中位值(M)：是一组数据的中间值，它是全部观察结果按大小顺序排列位次居中的那个数值。在全部观察值中，有一半的数值比它大，有一半的数值比它小。如果N为奇数，中位值是一个单一的中心值，为X(n+1)/2，[X(n/2)+X(n/2)+1]/2

四分位数间距(IQR)：是指上四分位数与下四分位数之差，其间包括了全部观察值的一半，其数值越大，说明分散程度愈大；反之，说明分散程度愈小。

上四分位值(Q3)：是指全部观察值中有四分之一的观察值比它大的一个值，为(3n/4+1/4)次序的观察值；

下四分位值(Q1)：是指全部观察值中有四分之一的观察值比它小的一个值，为(n/4+3/4)次序的观察值。

若一组观察值X1、X2，……XN，N为观察值的个数。按序以小到大排列该观察值为X{1}，X{2}，……X{N}，设A=1/4(N-1)、B=3/4(N-1)，则下四分位值Q1=(Q中+1)/2、上四分位值Q3=Q中+Q1-1

标准化四分位数间距(NIQR)：四分位数间距(IQR)乘以系数0.741 3，相当于一个标准差。

稳健变异系数(CV)：标准化四分位间距除以中位值，并以百分数表示，相当于经典的变异系数(标准差除以均值)。

稳健分析由稳健估计平均值、标准差迭代计算得出新的估计稳健平均值、标准差，直至过程收敛。当稳健标准差的第三位有效数字和稳健平均值相对应的数字在连续两次迭代中不再变化时，即可认为过程是收敛的。

四分位数间距(IQR)=上四分位值(Q3)-下四分位值(Q1)

标准化四分位数间距(NIQR)=IQR×0.741 3

稳健Z值等于观察值与中位值的差再除以NIQR。

注：因子0.741 3由标准正态分布得到。标准正态分布时均数为零，标准差为1，而这时四分位数间距是[-0.674 5，+0.674 5]，其宽度为1.349 0，故四分位数间距乘以(即0.741 3)相当于标准偏差。

实验室检测结果评价标准

利用Z比分数对参加实验室的能力进行判定，判定的标准分为3种情况：

①︱Z︱≦2为满意结果；

②2﹤︱Z︱﹤3为有问题的结果(可疑值)；

③︱Z︱≥3为不满意结果(离群值)。

6 结 语

该次能力验证活动为了能准确了解参加实验室日常分析的实际能力状况，对测试方法作了统一要求，各实验室均采用规定检测方法进行测试。反馈检测结果显示通过格拉布斯进行离群检测以及Z比分数稳健统计分析，显示各家测量结果无离群情况，并且比对结果均为“满意”，具体情况如表2所示。

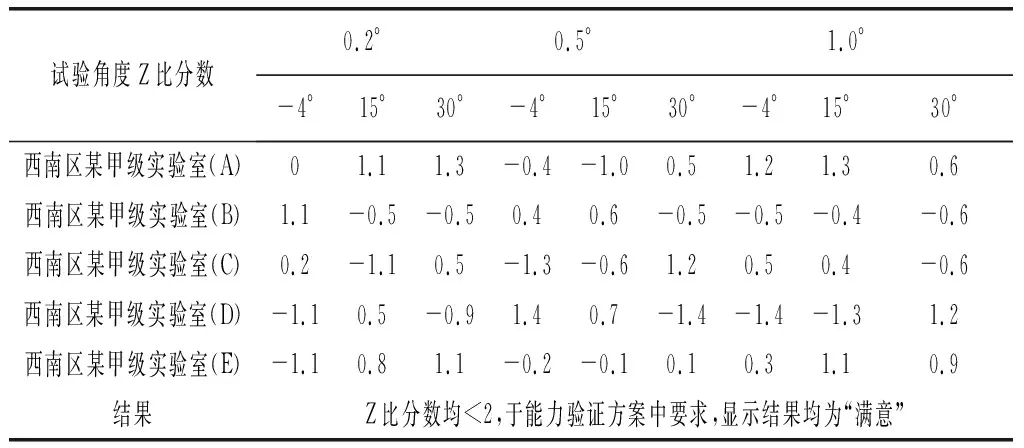
表2 Z比分数结果