考虑煤体弹-塑性变形的基本顶板初次破断结构特征
何富连,何文瑞,陈冬冬,谢生荣,李 辉,何常西
(中国矿业大学(北京) 能源与矿业学院,北京 100083)
工作面上覆基本顶的破断位置、破断顺序和破断形态对指导工作面安全回采以及邻侧区段巷道的煤柱宽度合理确定等意义显著[1-2]。
要研究基本顶的破断规律,需要明确两类问题:① 采用梁结构模型,还是板结构模型;② 模型的边界条件是固支、简支、弹性基础边界还是弹-塑性基础边界,这2个方面选择对科学合理的制定措施至关重要。
多年来,矿业科技工作者分别建立了基本顶在固支边界、简支边界、文克尔弹性基础边界(钱鸣高院士等根据煤体抗剪切能力弱等特点提出煤体近似符合文克尔弹性地基假设[1])等条件下的梁结构模型,据此分析了基本顶破断机理、破断形态、破断时的反弹压缩扰动,采场初次来压的结构特征及来压步距等问题[1,3-7];建立了基本顶在固支、简支及自由边界条件下的板结构模型,分析了基本顶的破断位置、破断顺序及“O-X”型破断形态特征等[8-15];初次破断前的基本顶四周处于上覆较软岩层和下伏直接顶与煤层的夹支状态,由于煤层的刚度小于甚至远小于基本顶的刚度,那么相同受力条件下煤层的压缩变形量大于甚至是远大于基本顶的压缩变形量,可见下伏煤层限制基本顶下沉的能力很弱,特别是煤层厚度较大且较软时,此时远无法满足固支边界条件假设,为了弥补此缺陷,构建并系统研究了文克尔弹性基础边界基本顶板结构首采工作面初次破断、周期破断、一侧采空与两侧采空时的破断规律及影响因素等[16-20],并得到了固支边界模型得不到的重要结论,这些研究从不同角度,基于不同的模型假设得到的研究结论对采矿工程实践起到了重要的指导作用。
但是,煤层开采后,基本顶悬顶区域周边一定深度范围内的煤体必然进入塑性状态,即全区域煤体并不能全部满足弹性基础边界条件假设。可见,全面考虑采空区周边煤体的弹-塑性变形,才能更符合基本顶初次破断特征,得到的结论才能更有效的指导实践。笔者通过构建弹-塑性基础边界条件下的基本顶板结构初次破断模型,基于有限差分方法研究煤体的塑化程度和塑化范围、基本顶厚度、弹性模量及未塑化煤体的弹性基础系数、悬顶跨度对基本顶板结构破断位置、破断顺序及整体形态特征的影响,对于认识基本顶初次破断过程及其结构形态具有重要价值。
1 基本顶边界条件类型
煤层开采后,悬顶区域的基本顶处于上覆与下伏岩层的夹支状态。若基本顶上下覆岩层的刚度为无穷大,可构建固支边界模型,如图1(a)所示;实际上,基本顶上下覆岩层的刚度小于甚至远小于基本顶的刚度,特别是煤层厚度较大且较软时是无法满足固支边界条件要求的,所以如图1(b)所示,可假设基本顶受到上下覆弹性岩层的夹支,即可构建弹性基础边界模型;对于实际的采矿工程问题,支撑基本顶的煤体浅部必然处于塑性状态,而围岩表层甚至处于破碎状态,深部煤体处于弹性状态,所以如图1(c)所示,可构建弹-塑性基础边界基本顶板结构模型,研究所得结论显然更符合实际。
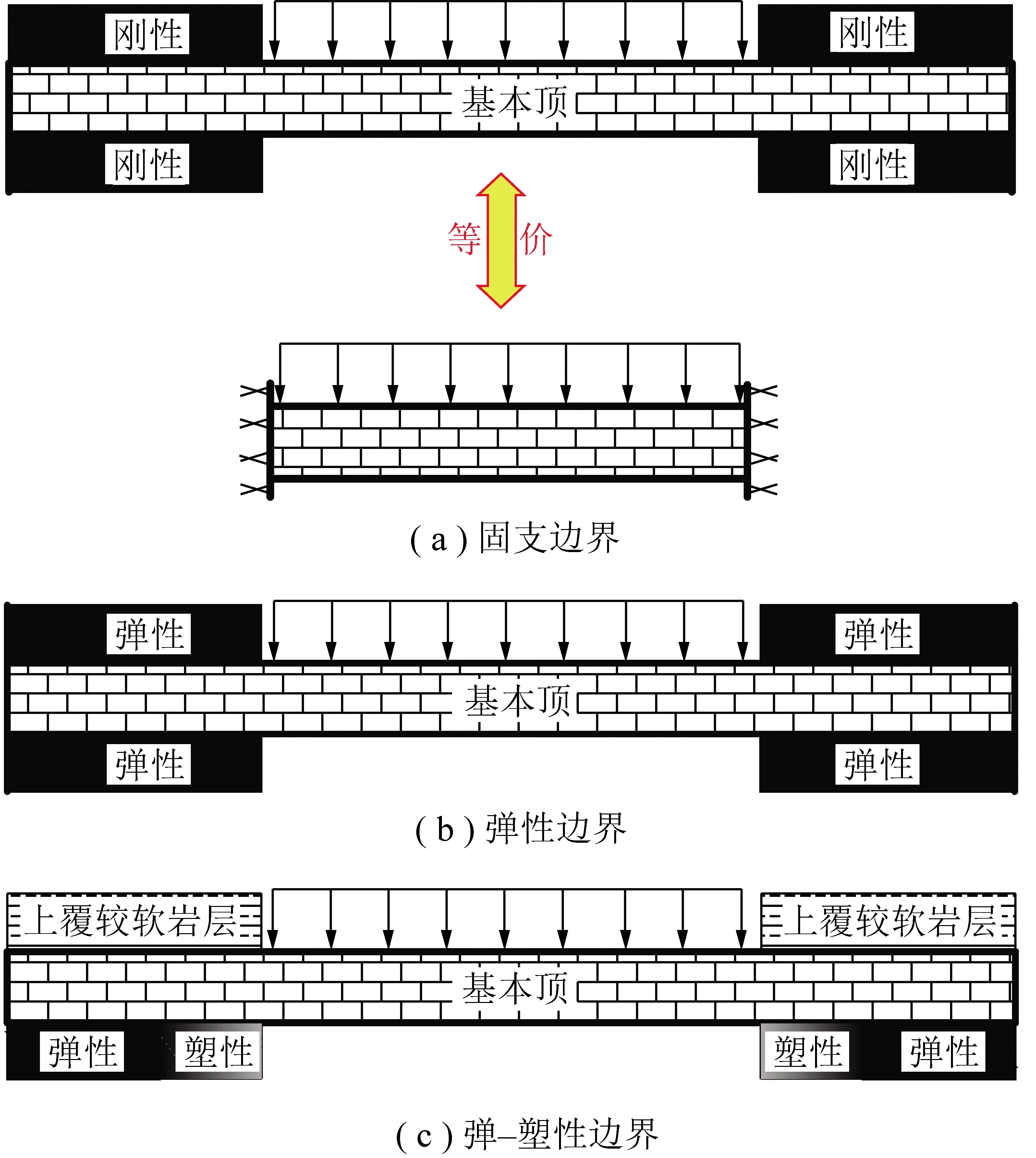
图1 基本顶边界条件对比Fig.1 Comparison ofmain roof boundary conditions
2 弹-塑性边界基本顶板结构力学模型
2.1 力学模型建立
根据弹性薄板力学假设[21]

(1)
式中,h为板厚度,m;l为板短边长度,m。
一般条件下采场上覆基本顶均满足上述要求,所以满足弹性薄板假设[21-22]。
开采区域周边的基本顶四周受到上下覆岩层的夹支,尤其是下伏煤层的基础系数是限制基本顶在煤体支撑区变形与破断的关键。通常条件下浅部煤体处于塑性状态,深部煤体处于弹性状态,即支撑基本顶的为周边弹-塑性煤体,而煤体塑化程度和范围必然对基本顶的破断特征有影响。
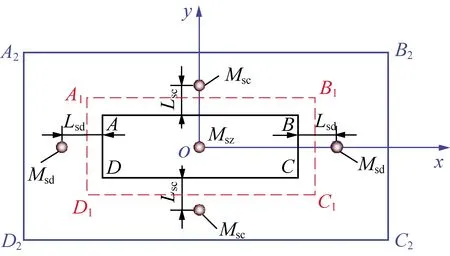
据此建立如图2所示的考虑煤体弹塑性变形的弹-塑性基础边界基本顶薄板初次破断力学模型,其中,ABCD区域为已经开采而基本顶悬顶未断区域、A1B1C1D1区域之内与ABCD区域之外为塑化煤体支撑区、A1B1C1D1区域之外而A2B2C2D2区域之内为弹性煤体支撑区,边A1B1,B1C1,C1D1及A1D1为弹-塑性煤体分界线,工作面的长度AB为2a、开采悬顶区的跨度AD为2b、外边界A2B2长度为2a2、外边界A2D2长度为2b2,长边塑性区的宽度为bs(即AB与A1B1或CD与C1D1之间的距离)、短边塑性区的宽度为as(即AD与A1D1,B1C1与BC之间的距离),长边弹-塑性分界边A1B1长度为2as+2a、短边弹-塑性分界边A1D1长度为2bs+2b;开采区域上覆基本顶承担载荷为q,其值为基本顶自重与上覆软岩层载荷之和。

图2 弹-塑性基础边界基本顶板结构力学模型Fig.2 Mechanical model of main roof structure with elastic-plastic foundation boundary
S悬顶区的基本顶挠度微分方程为
(2)
式中,ω(x,y)为S区域基本顶挠度函数;D为基本顶刚度。
S1塑性区的基本顶挠度微分方程为
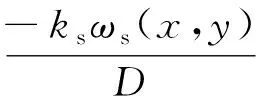
(3)
式中,ωs(x,y)为S1区基本顶挠度函数;ks为塑性区煤体基础系数(支撑系数)。
S2弹性区的基本顶挠度微分方程为

(4)
式中,ωt(x,y)为S2区基本顶挠度函数;kt为弹性区煤体基础系数(支撑系数)。
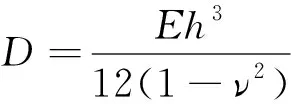
(5)
式中,ν为泊松比;E为基本顶弹性模量,GPa;h为基本顶厚度,m。
上述参数中,弹性煤体区的基础系数kt为煤体的弹性模量与煤体厚度的比值[7,20];煤体塑性区的宽度由文献[1]式(8-5)计算得到。ABCD边界线即浅部煤体基础系数(支撑系数)设为k0,k0代表了塑性区煤体的塑化程度,由于开采区浅部的煤体必然塑化甚至破碎,所以浅部煤体的基础系数k0值较小甚至为0(代表浅部破碎),而开采区周边深部煤体的塑化程度越来越小,即基础系数越来越大,直到弹性煤体区时煤体基础系数达最大值kt,设S1塑化区煤体基础系数为ks并满足关系式k0 2.2.1内边的边界条件 边DC,BC,AD及AB为基本顶塑性基础起始边界(也是已开采区与煤体区分界边),该边界上各点挠度同时满足悬顶区S的微分方程(2)与塑化区S1的微分方程(3),且各边上的挠度、截面法向线转角、弯矩与剪力分别连续,即满足: (6) 2.2.2弹-塑性分区的边界条件 边D1C1,B1C1,A1D1及A1B1为基本顶下伏煤体的弹-塑性分界边,边上各点挠度同时满足塑化区S1微分方程(3)与弹性区S2微分方程(4),且各边上的挠度、截面法向线转角、弯矩与剪力分别连续,即满足: (7) 2.2.3模型外边界的边界条件 图2中,对于首采面的基本顶板结构初次破断来说,开采区域的外边界A2B2C2D2距离开采悬顶区的距离要求不受或者基本不受开采区ABCD的扰动影响,由于外边界C2D2,B2C2,A2B2及A2D2不受开采扰动的影响,那么这些边不仅满足挠度为0,而且满足截面法向线转角为0,即满足式: (8) 要研究弹-塑性基础边界条件下的基本板结构破断规律,就需要得到偏微分方程(2)~(4)在边界条件(6)~(8)条件下的解,但是求出精确解极为困难,即便是弹性基础边界条件下的求解难度也很大[1,17-20]。众所周知,获得精确解并不是采矿工程问题所追求的,能求出近似解满足分析并解决采矿工程实际需求即可,而有限差分法就是符合该要求的有效方法[17-23]。 为了便于采用有限差分法具体求解偏微分方程(2)~(4)在边界条件(6)~(8)条件下的解,需要对差分节点进行编号,这样便于计算处理,图3为13节点编号图,中间特征节点为P点,节点间距为d。 图3 差分法节点编号Fig.3 Node number of difference method 基于差分节点编号图3可得式(2),(3)及(4)在特征节点P的差分方程分别为式(9),(10)及(11)。 20ωβ,δ-8(ωβ+1,δ+ωβ-1,δ+ωβ,δ+1+ωβ,δ-1)+ 2(ωβ+1,δ+1+ωβ+1,δ-1+ωβ-1,δ+1+ωβ-1,δ-1)+ (9) ωβ,δ-1)+2(ωβ+1,δ+1+ωβ+1,δ-1+ωβ-1,δ+1+ ωβ-1,δ-1)+ωβ+2,δ+ωβ-2,δ+ωβ,δ+2+ωβ,δ-2=0 (10) ωβ,δ-1)+2(ωβ+1,δ+1+ωβ+1,δ-1+ωβ-1,δ+1+ ωβ-1,δ-1)+ωβ+2,δ+ωβ-2,δ+ωβ,δ+2+ωβ,δ-2=0 (11) 一般条件下,对于实际开采边界范围以及采矿工程所要求的精度来说,外边界的范围不需要无穷远,只要是矩形区ABCD长边长度的3~5倍以上[1,17-20]即可近似满足式(8)要求的条件,且有限边界对于具体求解来说是有利的。所以可得外边界条件式(8)基于特征节点P的差分方程为式(12)。 (12) 根据基本顶板结构在开采悬顶区S、塑性区S1及弹性区S2的挠度偏微分方程的差分方程(9)~(11)可知,3个区域的挠度偏微分方程的差分方程均含有13个差分节点且挠度未知,而节点之间相互关联并通过边界条件来约束范围,由此可建立并求解基于边界条件的基本顶板结构挠度未知的13节点差分方程组,方程组的解即为各个节点的挠度解。显然,求解差分方程比直接求解偏微分方程要简单,为了满足计算精度要求,需要构建足够数量的差分方程(设节点间距d=0.2),那么虽然计算较易,但是方程数量多,此时可以采用软件Matlab[23-24]辅助计算,具体可采用sparse构建系数为稀疏矩阵联合代数方程组,然后采用函数gmres函数求解方程组,从而得到各个挠度未知节点的挠度解。 各个区域的所有挠度未知节点的挠度求解出来后,可得分量弯矩值,代入式(13)即可得到各个节点的主弯矩值,通过各个区域的主弯矩极值与弯矩极限Ms对比[1,17],可分析弹-塑性基础边界条件下的基本顶板结构是否发生破断,破断时的位置和破断顺序及影响因素等。 (13) 为系统研究弹-塑性基础边界基本顶板结构的破断规律,选取一特征参数采用上述计算方法计算并着重分析基本顶的主弯矩极值大小及位置特征。为了研究问题方便,设塑性区的煤体基础系数ks由浅部基础系数k0到弹性煤体区基础系数kt呈正相关线性增长;取工作面长度132 m(即图2中的AB长度)、推进距离44 m(即图2中的AD长度或跨度);基本顶的弹性模量E、厚度h、泊松比ν、载荷q分别为32 GPa,6.5 m,0.22,0.32 MPa;煤体浅部基础系数k0=0、煤体弹性区基础系数kt为1.5 GN/m3,周边煤体塑性区宽度(设为b0)为4 m。 通过计算得到各节点最大与最小主弯矩值并绘制出基本顶全区域主弯矩形态特征图。图4(a)为弹-塑性基础边界基本顶最小主弯矩M3的分布形态特征云图,图4(b)为弹-塑性基础边界基本顶最大主弯矩M1的分布形态特征云图。 根据图4基本顶各个区域的最大与最小主弯矩M1与M3的形态特征和数值分布规律可知: (1)开采区域长边与短边深入弹-塑性煤体区域基本顶板结构的最大与最小主弯矩M1与M3为负值,所以深入弹-塑性煤体区域基本顶板结构的上表面受拉应力而下表面受压应力,由岩石抗拉强度远小于抗压强度可知,基本顶深入弹-塑性煤体区的上表面先于下表面破断。 (2)开采区域长边与短边区域的绝对值最大主弯矩为最小主弯矩M3的相反数,且位置在深入弹塑性煤体区域而不是固支边界模型得到的沿着煤壁。 (3)开采悬顶区域中部基本顶的最大与最小主弯矩M1与M3均为正值,所以该区域基本顶的上表面受压应力而下表面受拉应力,且下表面先于上表面破断。 (4)基本顶中部区域的最大主弯矩在开采区域的中点(坐标为图2中O点坐标(0,0)位置),且数值为对应点主弯矩M1。 不同参数条件下弹-塑性基础边界基本顶板结构全区域的最大与最小主弯矩的分布形态与图4相似,且开采区域长边与短边主弯矩极值的位置也处于弹-塑性煤体区,开采区域中部的最大主弯矩在开采区的中点,所以要得到弹-塑性基础边界基本顶板结构的破断规律可以通过研究各个特征区域的主弯矩极值的大小和位置及随影响因素的变化特征来分析。 图4 弹-塑性基础边界基本顶板结构主弯矩云图Fig.4 Cloud chart of main bending moment of main roof plate structure with elastic-plastic foundation boundary 根据上述分析结果,建立如图5所示的弹-塑性基础边界基本顶主弯矩极值位置图,其中,中部区域的主弯矩极值为中点(0,0)位置处的最大主弯矩M1,并设Msz=M1|(0,0);长边区域绝对值最大主弯矩为主弯矩M3极值的负数,其深入煤体距离为Lsc,即距离AB边或CD边的长度为Lsc,设该极值为Msc,那么满足Msc=|M3|(0,b+Lsc)|与Msc=|M3|(0,-b-Lsc)|;短边区域绝对值最大主弯矩为主弯矩M3极值的负数,该极值深入煤体距离为Lsd,即距离AD边或BC边的长度为Lsd,设该主弯矩极值的绝对值为Msd,那么满足Msd=|M3|(a+Lsd,0)|,Msd=|M3|(-a-Lsd,0)|。可见,弹-塑性基础边界基本顶板结构的主弯矩极值主要在开采区中部、长边弹-塑性煤体区及短边弹-塑性煤体区,分析这几个特征区域的主弯矩Msz,Msc与Msd的大小及所在位置Lsc与Lsd即可分析弹-塑性基础边界基本顶板结构的初次破断顺序、破断位置及整体破断规律。 图5 弹-塑性基础边界基本顶主弯矩极值位置Fig.5 Location of the extreme value of the main roof main bending moment with the boundary of elastic-plastic foundation 弹-塑性基础边界条件下,基本顶板结构的初次破断规律主要受基本顶的厚度h、弹性模量E、跨度L(L越大代表基本顶强度越大,可悬顶距离越大)、实体煤区弹性煤体基础系数kt、煤体塑化范围as,bs及浅部煤体基础系数k0影响,本文采用控制变量法着重研究这些因素对弹-塑性基础边界基本顶板结构初次破断特征的影响,最后研究这些因素的权重关系。 由于采用控制变量法进行研究,以下所采用的计算基础参数未经说明更改的均为:工作面长度及跨度分别为132,44 m;基本顶的弹性模量E、厚度h、泊松比ν及载荷q分别为32 GPa,6.5 m,0.22及0.32 MPa;浅部煤体的基础系数k0及未塑化弹性煤体基础系数kt分别为0及1.5 GN/m3,周边煤体塑性区宽度as及bs均为4 m。 如图6所示,未塑化的弹性煤体基础系数kt不仅可以改变基本顶的破断位置且可改变基本顶的破断顺序。 图6 主弯矩及位置随kt变化规律Fig.6 Variation rule of main bending moment and position with kt (1)基本顶破断位置方面:随kt值增大,长边主弯矩Msc深入煤体距离Lsc由大于煤体塑性区宽度bs过渡到逐步小于bs,这说明kt较小时长边破断线在未塑化的弹性煤体区上覆,kt较大时长边破断线在塑化煤体区上覆;kt值越小,长边破断线深入煤体距离Lsc越大,即煤体越软,约束基本顶整体下沉变形的能力越弱,破断线越超前煤壁,此时与固支边界模型的差距也越大;短边破断位置Lsd与长边Lsc的变化规律相同。 (2)基本顶破断顺序及形态方面:随kt值增大,基本顶中部主弯矩Msz减小,而长边与短边的主弯矩Msc与Msd逐渐增大,但增长幅度小于降低幅度;①kt较小时,Msz>Msc>Msd,主弯矩达到弯矩极限Ms时,基本顶破断顺序为:中部下表面→长边深入弹性煤体区上表面→短边深入弹性煤体区上表面,最终在弹性煤体区上方形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(d),(e)所示;②kt较大时,Msc>Msz>Msd,基本顶破断顺序为:长边深入塑化煤体区上表面→中部下表面→短边深入塑化煤体区上表面,最终在塑化煤体区上覆形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(a)~(c)所示;③kt=kts时,基本顶“O”型断裂圈在煤体弹-塑性分界线区域,如图7(f),(g)所示;④kt=ktj时,Msz=Msc=Mj,即存在基本顶中部与长边同时破断的情况。 图7 弹-塑性基础边界基本顶板结构破断特征Fig.7 Fracture characteristic diagram of main roof plate structure with elastic-plastic foundation boundary 而固支边模型得到基本顶断裂线沿着煤壁与kt值无关,可见固支边界模型所得结论与实际差距较大,尤其是破断位置及破断顺序方面。 如图8所示,基本顶的厚度h不仅可以改变基本顶的破断位置且可改变基本顶的破断顺序。 (1)基本顶破断位置方面:随h值增大,长边主弯矩Msc深入煤体距离Lsc由小于煤体塑性区宽度bs过渡到大于bs,这说明h较大时长边破断线在未塑化的弹性煤体区上覆,h较小时长边破断线在塑化煤体区上覆;h值越大,长边破断线深入煤体距离Lsc越大,即基本顶越厚,需要更大范围内的煤体约束基本顶才能发生破断,此时与固支边界模型的差距也越大;短边破断位置Lsd与长边Lsc的变化规律相同。 (2)基本顶破断顺序及形态方面:随h值减小,基本顶中部主弯矩Msz减小,而长边与短边的主弯矩Msc与Msd逐渐增大;①h较小时,Msc>Msz>Msd,基本顶破断顺序为:长边深入塑化煤体区上表面→中部下表面→短边深入塑化煤体区上表面,最终在塑化煤体区上覆形成“O”型断裂圈,整体为“O-X”型破断形态,如图7(a)~(c)所示;②h较大时,Msz>Msc>Msd,基本顶破断顺序为:中部下表面→长边深入弹性煤体区上表面→短边深入弹性煤体区上表面,最终在弹性煤体区上方形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(d),(e)所示;③h=hs时,基本顶“O”型断裂圈在煤体弹-塑性分界线区域,如图7(f),(g)所示;④h=hj时,Msz=Msc=Mj,即存在基本顶中部与长边同时破断的情况。基本顶弹性模量E对破断规律的影响与h相似。 图8 主弯矩及位置随基本顶厚度变化规律Fig.8 Variation rule of main bending moment and position with thickness of main roof 而固支边模型得到基本顶断裂线沿着煤壁,与h及E值无关,可见固支边界模型所得结论与实际差距较大,尤其是破断位置及破断顺序方面。 图2中,开采悬顶跨度越大,即代表基本顶的强度越大,那么研究跨度L对弹-塑性基础边界基本顶破断规律的影响就是间接研究基本顶强度对破断规律的影响。由图9可得: (1)基本顶破断位置方面:随L值增大,长边主弯矩Msc深入煤体距离Lsc由大于煤体塑性区宽度bs过渡到逐步小于bs,这说明L较小时长边破断线在未塑化的弹性煤体区上覆,L较大时长边破断线在塑化煤体区上覆;L值越小,长边破断线深入煤体距离Lsc越大,此时与固支边界模型的差距也越大;短边破断位置Lsd与长边Lsc的变化规律相同。 (2)基本顶破断顺序方面:①L较大时,Msc>Msz>Msd,基本顶破断顺序为:长边深入塑化煤体区上表面→中部下表面→短边深入塑化煤体区上表面,最终在塑化煤体区上方形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(a)~(c)所示;②L较小时,Msz>Msc>Msd,基本顶破断顺序为:中部下表面→长边深入弹性煤体区上表面→短边深入弹性煤体区上表面,最终在弹性煤体区上方形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(d),(e)所示;③L=Ls时,基本顶“O”型断裂圈在煤体弹-塑性分界线区域,如图7(f),(g)所示;④L=Lj时,Msz=Msc=Mj,即存在基本顶中部与长边同时破断的情况。 而固支边模型得到基本顶断裂线沿着煤壁,与L值无关,可见固支边界模型所得结论与实际差距较大,尤其是破断位置及破断顺序方面。 如图10所示,煤体的塑化范围b0不仅可以显著改变基本顶的破断位置且可以改变基本顶的破断顺序。 图9 主弯矩及位置随跨度L变化规律Fig.9 Variation rule of main bending moment and position with the span L 图10 主弯矩及位置随b0变化规律Fig.10 Variation rule of main bending moment and position with b0 (1)基本顶破断位置方面:随煤体塑化范围b0值增大,长边主弯矩Msc深入煤体距离增大;当b0=b0s时,Lsc=L0sc=b0s,即煤体塑化范围与基本顶长边断裂线深入煤体距离相等,可见,b0较小时长边破断线在弹性煤体区上覆,b0较大时长边破断线在塑化煤体区上覆;b0越大,长边破断线深入煤体距离Lsc越大,即煤体塑化范围越大,约束基本顶下沉变形的能力越弱,破断线越深入煤壁,此时与固支边界模型的差距也越大;短边破断位置Lsd与长边Lsc的变化规律相同。 (2)基本顶破断顺序方面:煤体塑化范围b0增大时,各个主弯矩均增大,这相当于煤体支撑基本顶的能力减弱(或说悬顶程度增大),所以各个主弯矩均增大;① 塑化范围b0较小时,满足Msc>Msz>Msd,基本顶破断顺序为:长边深入弹化煤体区上表面→中部下表面→短边深入弹性煤体区上表面,最终在弹性煤体区上方形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(d),(e)所示;② 塑化范围b0较大时,满足Msz>Msc>Msd,基本顶破断顺序为:中部下表面→长边深入塑化煤体区上表面→短边深入塑化煤体区上表面,最终在塑化煤体区上覆形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(a)~(c)所示;③b0=b0s=L0sc时,“O”型断裂圈在煤体弹-塑性分界线区域,如图7(f),(g)所示;④b0=b0j时,Msz=Msc=Mj,即存在基本顶中部与长边同时破断的情况。 而固支边模型与弹性基础边界模型均无法研究煤体塑化范围对基本顶板结构破断位置及规律的影响,可见传统模型所得结论有局限性。 由图11可知煤体的塑化程度(采用浅部塑化煤体基础系数k0来表征)不仅可以显著改变基本顶的破断位置且可以改变基本顶的破断顺序: (1)基本顶破断位置方面:随煤体塑化程度增大(即k0减小),长边主弯矩Msc深入煤体距离Lsc由小于煤体塑化宽度bs过渡到逐步大于bs,这说明k0较小时长边破断线在未塑化的弹性煤体区上覆;k0较大时长边破断线在塑化煤体区上覆;k0值越小,长边破断线深入煤体距离Lsc越大,即煤体塑化程度越大,约束基本顶下沉变形的能力越弱,破断线越深入煤体,此时与固支边界模型的差距也越大;短边破断位置Lsd与长边Lsc的变化规律相同。 (2)基本顶破断顺序方面:塑化程度增大时(即k0减小),各个主弯矩均增大,且长边Msc增长程度大于中部Msz的增长幅度,这相当于浅部煤体支撑基本顶的能力减弱,基本顶悬顶程度相对增大,所以各个主弯矩均增大;① 塑化程度较大时,满足Msc>Msz>Msd,基本顶破断顺序为:长边深入弹性煤体区上表面→中部下表面→短边深入弹性煤体区上表面,最终在弹性煤体区上覆形成“O”型断裂圈,整体破断形态为“O-X”型,如图7(d),(e)所示;② 塑化程度较小时,满足Msz>Msc>Msd,基本顶破断顺序为:中部下表面→长边深入塑化煤体区上表面→短边深入塑化煤体区上表面,最终在塑化煤体区上覆形成“O”型断裂圈,整体为“O-X”型破断形态,如图7(a)~(c)所示;③k=k0s时,基本顶“O”型断裂圈在煤体弹-塑性分界线区域,如图7(f),(g)所示;④k0=k0j时,Msz=Msc=Mj,即存在中部与长边同时破断的情况。 图11 主弯矩及位置随k0变化规律Fig.11 Variation rule of main bending moment and position with k0 而固支边模型与弹性基础边界模型均无法研究煤体塑化程度对基本顶板结构破断位置及规律的影响,可见传统模型所得结论有局限性。 上文采用控制变量法分析了基本顶的厚度h、弹性模量E、跨度L、实体煤区未塑化的弹性煤体基础系数kt、煤体塑化范围及煤体塑化程度k0对弹-塑性基础边界基本顶板结构破断特征及规律的影响。下面分析影响因素之间存在的关系。 如图12所示,同时改变kt与h的大小,且满足kt与k0取任意比值不变(图中两者比值为10:1),kt与h3也取任意比值不变,可以得到弹-塑性基础边界基本顶板结构各个主弯矩大小及位置均不改变,破断顺序和位置也不变。 图12 主弯矩及位置的影响因素权重关系Fig.12 Weight relation of main bending moment and position 可见,虽然弹-塑性基础边界基本顶板结构破断的影响因素复杂,但是k0,kt与h3之间满足上述“比值不变”条件时,具有破断规律不变的特征。 弹性基础边界模型与弹-塑性基础边界模型都考虑了煤体可变形的实际特征,但是考虑煤体塑化程度和塑化范围的模型得到传统模型得不到的诸多结论,更符合实际且对实践的指导意义显著,下面为2类模型的对比说明。 (1)破断位置方面。2类模型都可以得到基本顶深入煤体断裂,但是弹性基础边界模型只能得到断裂线在弹性煤体区,而本文模型得到基本顶的断裂线位置主要有3种:① 弹性煤体区;② 塑性煤体区;③ 煤体的弹塑性分界线。本文模型更加全面且符合实际,对工程实践的指导意义更大。 (2)破断顺序方面。基本顶的初次破断位置都有2类:① 长边超前煤壁区的基本顶上表面;② 基本顶悬顶区中部的下表面,但煤体的塑化范围和塑化程度也显著影响基本顶的破断位置和破断顺序,而弹性基础边界模型无法得到实际工程中煤体必然塑化引起基本顶破断顺序改变的结论。 (3)破断形态方面。基本顶岩板整体破断形态都是“O-X”型,而本文模型得到基本顶O型圈位置有3类:① 在弹性煤体区上覆;② 在塑性煤体区上覆;③ 在煤体的弹塑性分界线上覆,而弹性基础边界模型只能得到O型圈在煤体的弹性区上覆,显然本文模型得到的结论更加全面且符合实际。 研究清楚符合实际围岩关系的基本顶板结构的破断顺序、位置及整体形态特征,对于预防顶板大面积切顶来压事故及合理确定工作面侧方巷道的位置等至关重要。 基于弹-塑性基础边界基本顶板结构模型,下面选取2个方面,即从工作面推进方向基本顶断裂位置和工作面短边区域基本顶断裂位置角度说明本文力学模型的重要工程意义。 现给出一具体算例进行说明,图2中,一工作面的跨度为42 m、工作面长度为200 m,基本顶厚度为10 m、弹性模量为35 GPa,弹性煤体基础系数为1.2 GN/m3,周边塑性区煤体宽度为5 m,浅部煤体基础系数为0(即浅部煤体基本无承载能力),塑性区煤体由浅部到深部的基础系数按线性增长,基于本文的计算方法和破断准则,得到如下基本结论,并与传统模型进行对比分析。 本文的力学模型得到,基本顶超前煤壁的断裂位置Lsc为6.6 m(与实际值接近),断裂线处在煤体的弹性区(图13(b)),而传统的固支边界模型得到基本顶的断裂线沿着长边煤壁(图13(a)),显然在基本断裂位置方面传统模型不能反应工程实际。 图13 工作面长边区基本顶断裂位置对比Fig.13 Comparison of main roof fracture positions at the long side area of working face 工作面推进方向上,基本顶是超前煤壁破断的,那么破断时,前方有弹-塑性煤体的支撑,断裂时工作面并不会显著来压,当支架推进到断裂线区域时,压力显著增大,这说明,工作面来压是个过程且破断与显著来压之间有时间差,那么基本顶刚断裂时即预警,提前采取措施加强支架控制,防止工作面大面积切顶事故的发生;而传统模型得到,基本顶的断裂线沿着煤壁,显然不能从断裂位置角度得到有助于实践的结论,且不能有效指导提前采取措施预警工作面大面积切顶事故的发生。 同时由上文得到的煤体塑化程度和范围越大时,开采区域周边基本顶的主弯矩越大,且主弯矩深入煤体的距离越大的结论明确表明了在实践过程中,采取对煤体的弱化措施不仅可以加速基本顶的破断(减小来压步距),而且破断线更加深入煤体,基本顶刚破断时可以减弱对支架的冲击,这对工作面顶板的安全控制有重要指导意义。 本文的力学模型得到,工作面侧向基本顶深入煤体的断裂位置Lsd为6.9 m(与实际值接近),处在煤体的弹性区(图14(b)),而传统的固支边界模型得到基本顶的断裂线沿着短边煤壁(图14(a)),这说明传统模型在基本断裂位置方面不能有效反应工程实际。 基本顶侧向断裂线的位置对沿空巷道位置选择意义重大,直接决定了沿空巷道顶板结构稳定性程度。传统的固支边界模型无法得到短边区域基本顶的断裂位置在深入煤体区域;弹性基础边界板结构模型虽然可以得到基本顶的断裂位置在深入煤体处,但是却得不到基本顶断裂线在煤体的弹性区还是塑性区或者弹-塑性分界面。 图14 工作面短边区基本顶断裂位置对比Fig.14 Comparison of main roof fracture positions in short side of working face 沿空巷道位置选择不仅与基本顶在侧方的断裂线位置有关,还与基本顶断裂线在煤体的弹性区还是塑性区有关,如图14(b)所示,若在采空区邻侧掘进下一区段回采巷道,煤柱宽度Lm与基本顶在侧方的断裂位置Lsd的大小关系(有3种:Lm>Lsd,Lm 可见,本文构建的弹-塑性基础边界模型可以有效弥补传统固支边界与弹性基础边界板结构模型的缺陷,不仅可以有效得到基本顶深入煤体的断裂位置,而且可以得到断裂位置在弹性煤体区还是塑性煤体区,这对于巷道位置选择,煤柱宽度留设等均有重要指导意义。 (1)弹-塑性基础边界基本顶板结构的破断位置、顺序及形态,均随煤体的塑化范围和塑化程度、弹性煤体的基础系数、悬顶跨度、基本顶的厚度和弹性模量而改变。 (2)煤体塑化程度和塑化范围增大,基本顶各个区域的主弯矩绝对值均增大,即基本顶更易发生破断,且基本顶在悬顶区周边破断位置深入煤体距离增大,这对于工程实践中控制基本顶断裂线深入煤体位置和来压步距具有指导意义。 (3)煤体塑化范围增大,中部主弯矩增长程度大于长边的,即塑化范围大时,基本顶中部区域更易先破断;煤体塑化程度增大,基本顶长边主弯矩增长程度大于中部的,即煤体塑化程度大时,基本顶长边更易先破断。 (4)煤体塑化范围及浅部塑化煤体基础系数较大时,基本顶的破断位置及顺序为:开采悬顶区中部→长边深入塑化煤体区→短边深入塑化煤体区,在塑化煤体区上覆形成“O”型断裂圈;反之,基本顶的破断位置及顺序为:长边深入弹性煤体区→开采悬顶区中部→短边深入弹性煤体区,在弹性煤体区上覆形成“O”型断裂圈,最终均形成“O-X”型破断形态。 (5)浅部塑化煤体基础系数k0与弹性煤体基础系数kt为任意比值不变且kt与h3为任意比值不变时,基本顶的主弯矩大小及位置均不变,基本顶的破断规律不变。 本文的力学模型,弥补了传统的固支边界板结构模型和弹性基础边界板结构模型的缺陷。2.2 边界条件


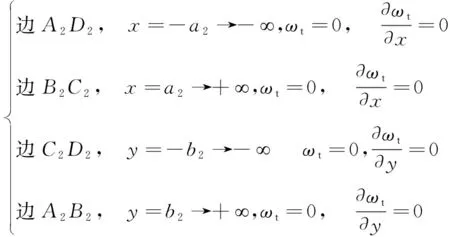
3 弹-塑性基础边界板结构模型计算法
3.1 差分节点编号
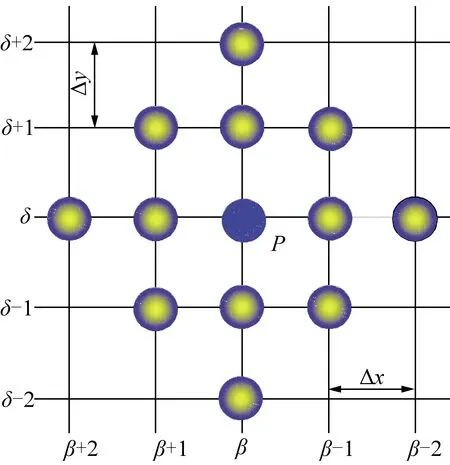
3.2 挠度方程的差分方程
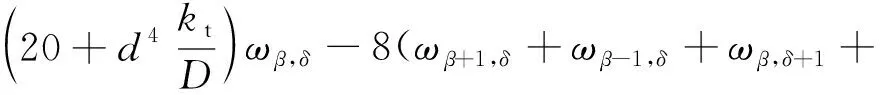
3.3 外边界条件方程的差分方程
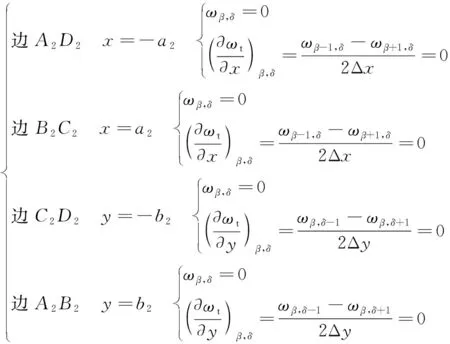
3.4 弹-塑性基础板结构模型求解及破断指标
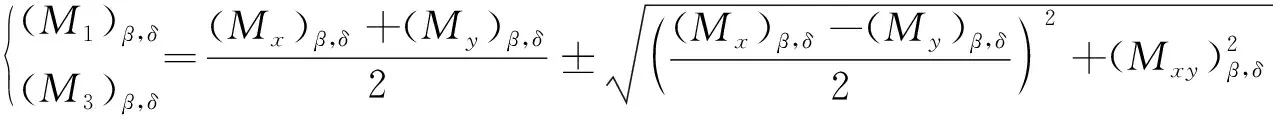
4 弹-塑性基础基本顶板结构模型分析
4.1 弹-塑性基础边界基本顶板结构的主弯矩形态特征
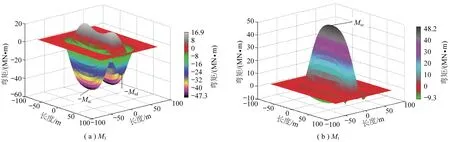
4.2 破断特征的弹性煤体基础系数kt效应
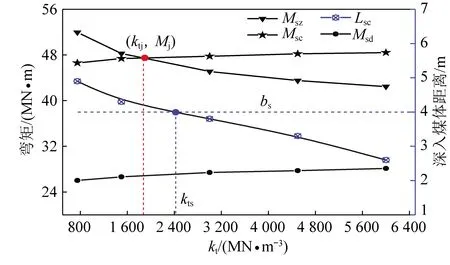
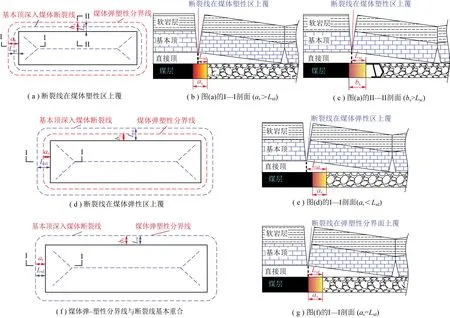
4.3 破断特征的基本顶厚度效应
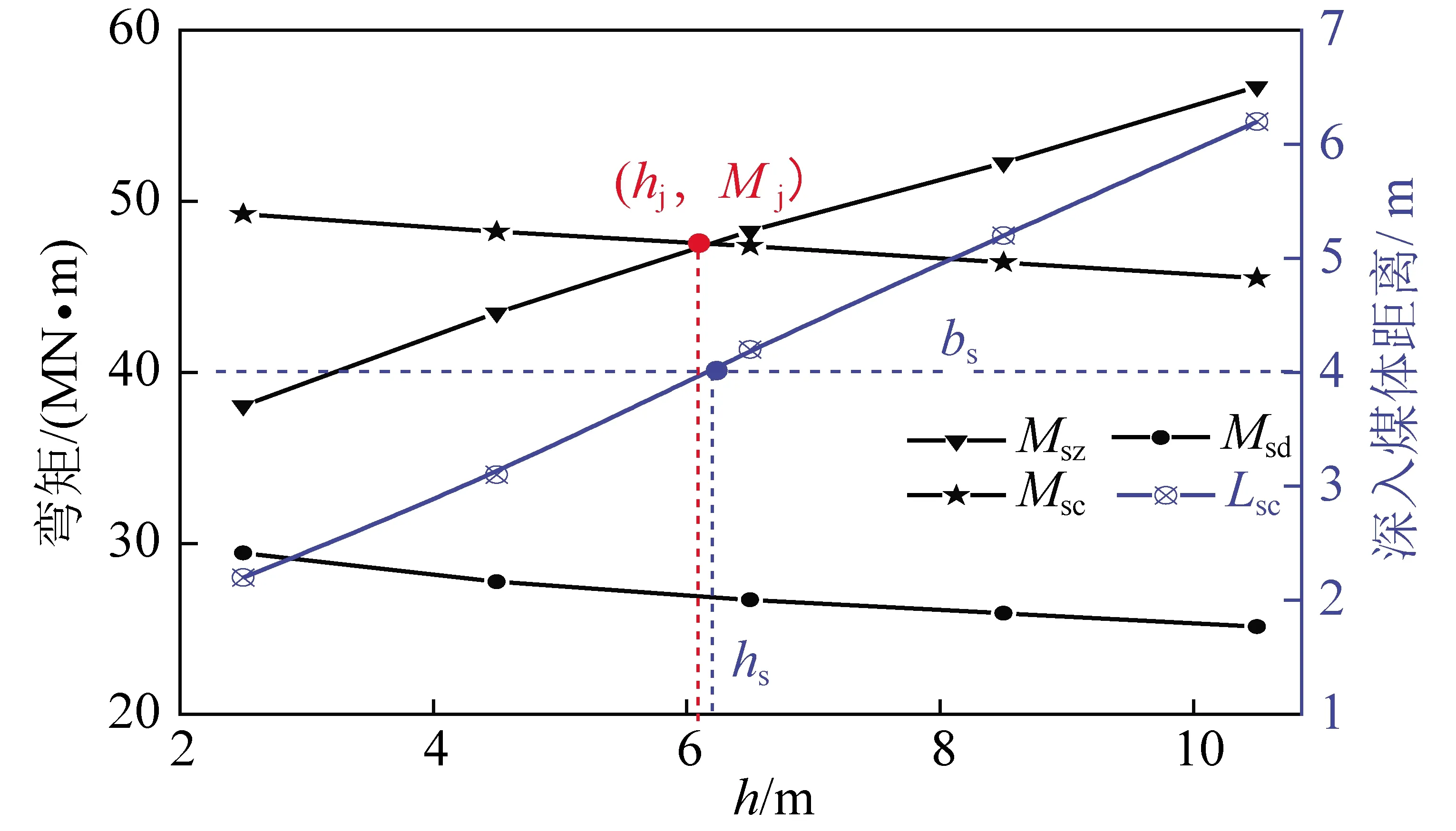
4.4 破断特征的跨度效应
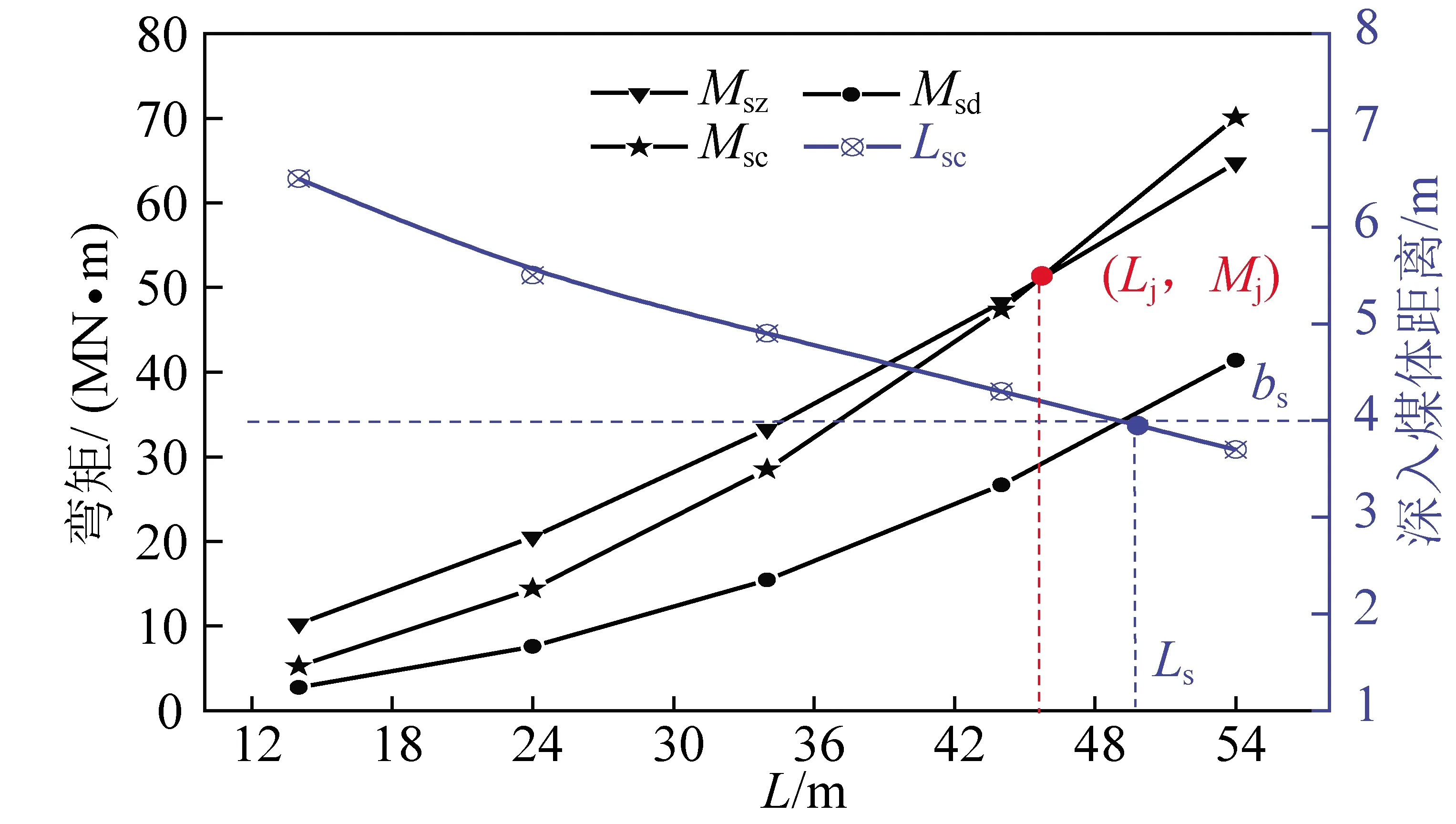
4.5 破断特征的煤体塑化范围b0效应
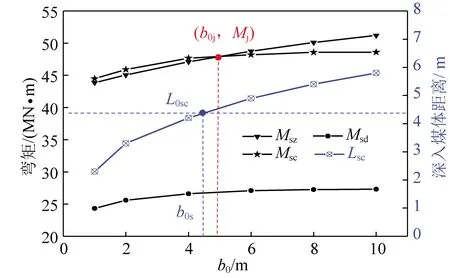
4.6 破断特征的煤体塑化程度效应

4.7 破断特征的影响因素之间存在的关系(比值不变规律)
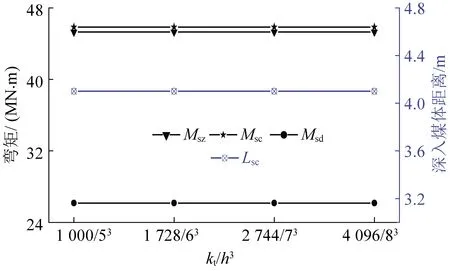
4.8 与弹性基础边界模型破断规律对比分析
5 工程算例分析
5.1 工作面推进方向基本顶板结构破断位置的工程意义

5.2 工作面侧向(短边区)基本顶板结构破断位置的工程意义

6 结 论

