节理岩体对SV波传播的影响

路世伟，刘洪宇，孙金山，周传波

(1.长江大学城市建设学院，湖北 荆州 434023；2. 江汉大学湖北(武汉)爆炸与爆破技术研究院，武汉 430056；3.中国地质大学工程学院，武汉 430074)

天然的节理岩体并不是均质体，而是由许多的不连续面组成的。这其中包括断层、节理、裂隙等，这就造成了天然节理岩体不同的各项指标，对节理岩体的不均匀性和不连续性都有着很大的影响。

国内外许多学者从理论和试验两方面对节理面对应力波传播影响进行了深入的研究。在计算中，平面节理岩体中的SV波是应用最普遍的应力波，影响很大，所以研究SV波在节理面上的传播有很重要的意义。孙金山等[1]运用数值模拟的方法分析了爆破地震波中P波对邻近圆形隧道动力扰动特征。赵坚等[2]则用 UDEC 模拟了爆炸波在节理岩体中的传播。张艳玲等[3]利用LS-DYNA有限元分析软件,通过三维数值模拟,分别从振速、能量和强度等方面研究节理对爆破应力波传播的影响。薛小蒙等[4]利用ANSYS数值软件,研究了不同厚度、角度和充填材料的结构面对应力波的影响规律。也有许多学者[5-6]对应力波在不同工况下的传播及影响进行了研究。王卫华等[7]、林发荣等[8]、丁梧秀等[9]对节理单元对波的影响及其稳定性进行了分析。林建生等[10]、许建聪等[11]、简文彬等[12]、章在墉等[13]、胡钧等[14]对波在不同地区的传播进行了分析。

在解决岩体及岩石动力学的防护问题上，节理对波能量的衰减成为了人们最关心的问题之一。研究这一问题可以提高工程实践中波对工程影响的准确度和可靠性，且对岩石动力学、防灾减灾工程等学科具有基础性意义。

1 计算模型

为简化计算，选择含2条平行节理的节理岩体为研究对象，建立尺寸为36 m×12 m的平面应变问题数值模型(见图1)，节理倾角α=90°，岩体的体积模量为6.36 GPa，剪切模量为1.36 GPa，密度取值为2 650 kg/m3，入射波频率为50 Hz。设节理间距为d，监测点间距为d/5。在节理1前、节理间以及节理2后共布置了6个监测点(见图2)。

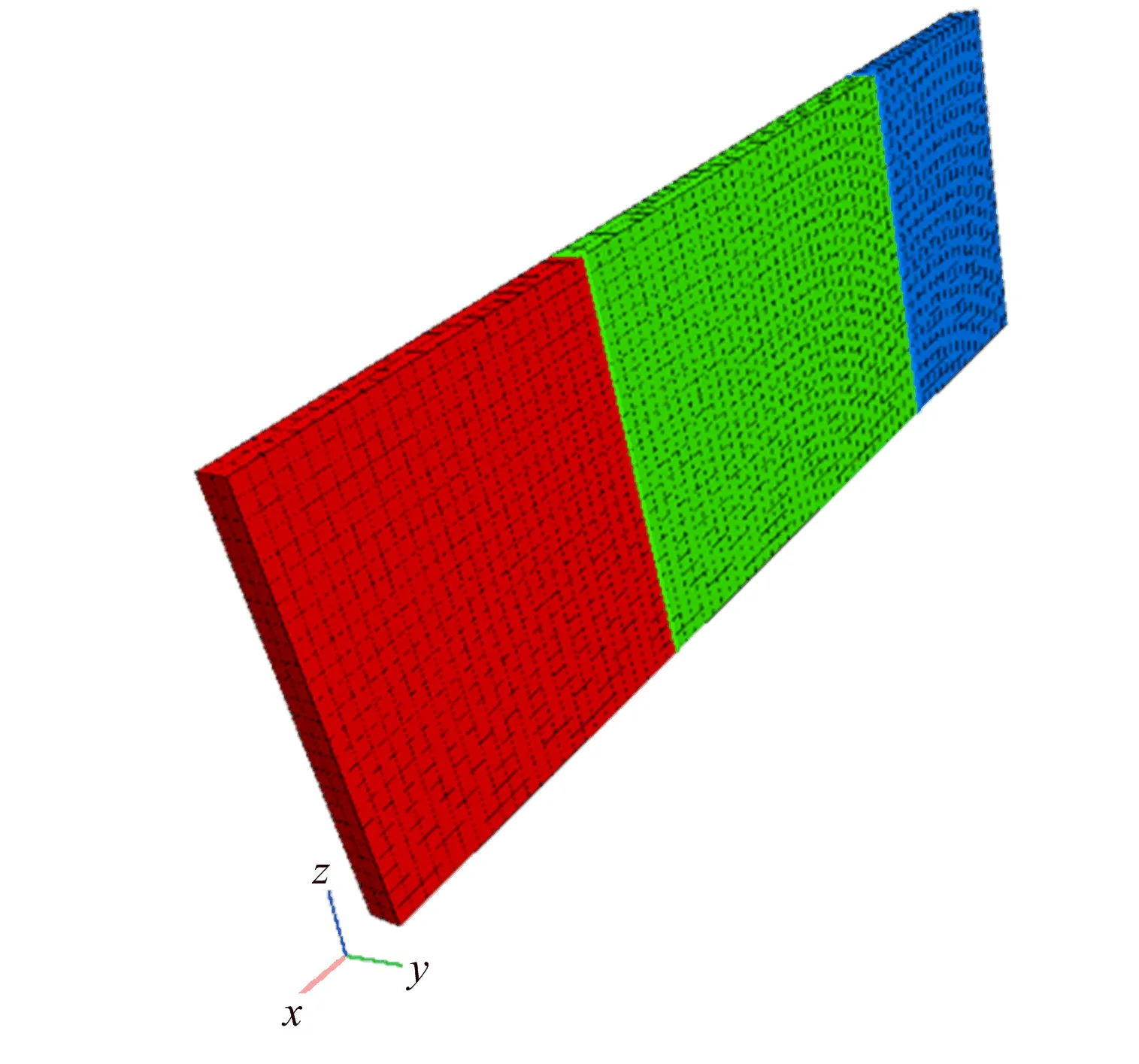
图1 双平行节理岩体数值模型Fig.1 Numerical model of rockmass with two parallel joints

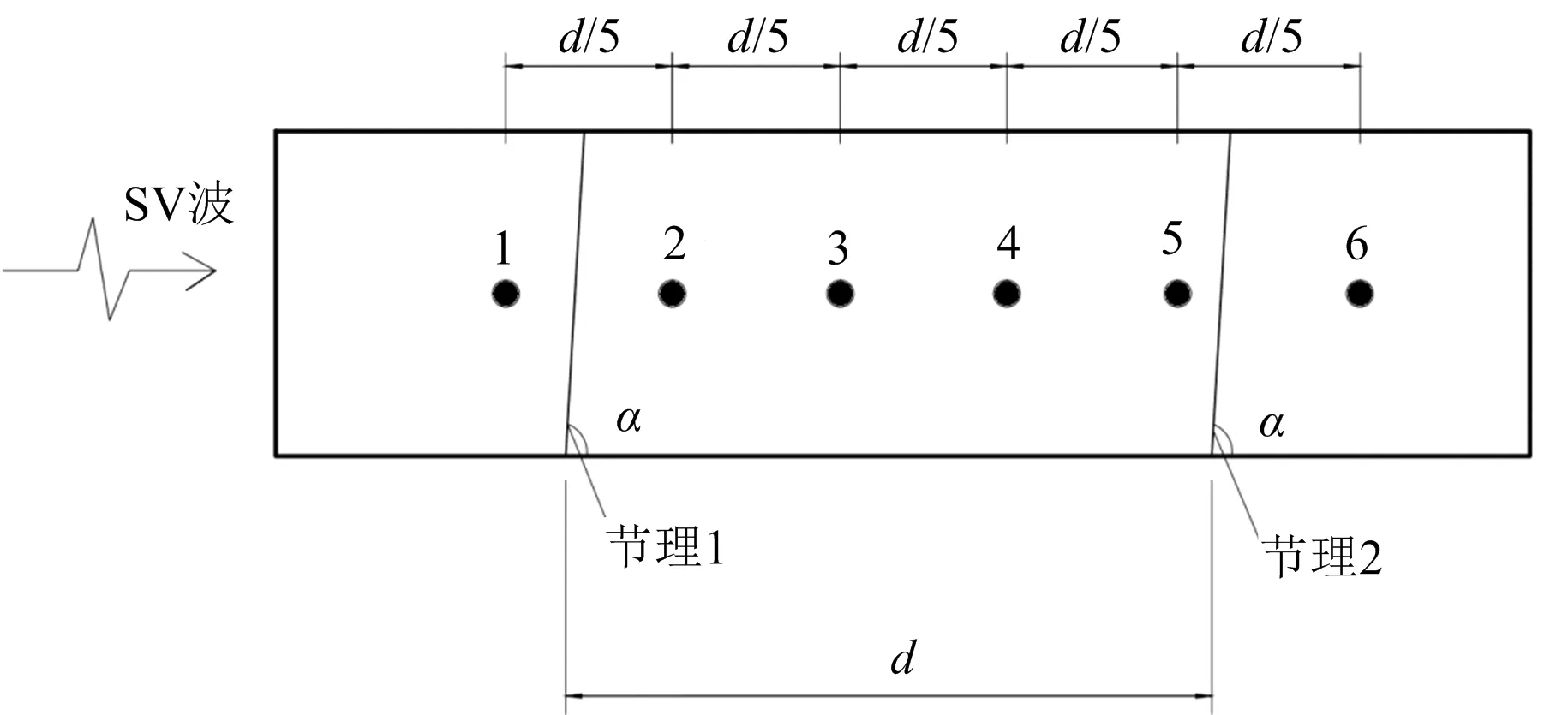
注：1～6为监测点编号图2 监测点布置Fig.2 Layout of monitoring points

2 模型可靠性验证

为验证数值计算结果的可靠性，选择单节理模型计算结果与理论分析结果进行对比，通过FLAC3D数值模拟软件建立单节理岩体数值模型(见图3)。当SV波垂直入射时，反射系数和透射系数理论计算公式[15]分别为

(1)

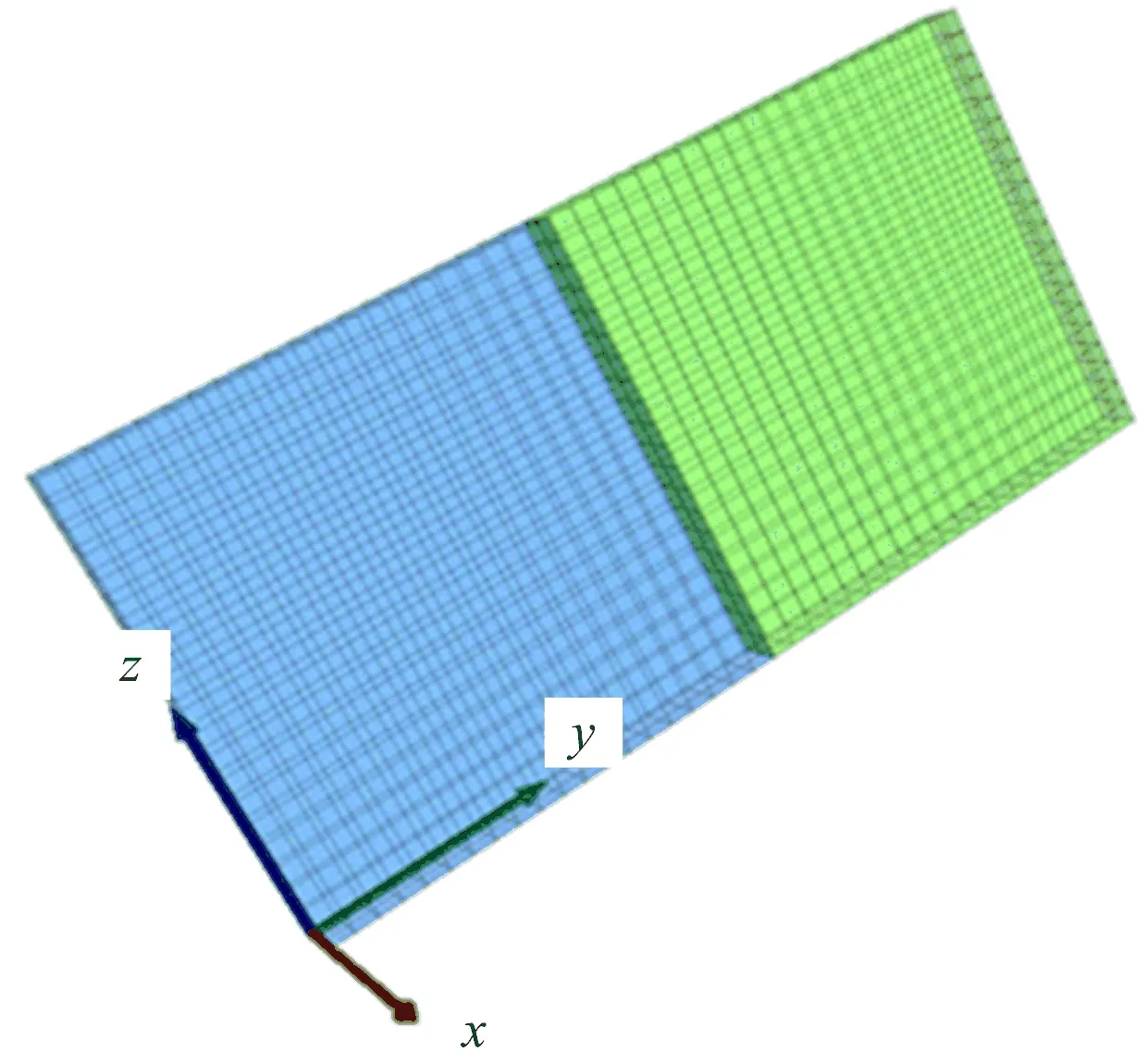
图3 单节理岩体数值模型Fig.3 Numerical model of rockmass with a single joint

不同节理刚度情况下透射系数和反射系数的大小变化情况如图4所示，当0.5≤K<3.0时，透射系数会逐渐增大；当K≥3.0时，透射系数趋于1，相当于SV波的全部透射，但是在节理岩体中发生反射的概率相当小，趋近于0。相反，反射系数逐渐减小，在K≥3.0时趋近于0，与理论计算结果基本上吻合。由以上分析可知，FLAC3D的模拟结果能够准确地反映平面SV波在节理岩体中的传播规律，利用基于FLAC3D数值模拟软件研究平面SV波在节理岩体中的传播规律的研究是可行的。

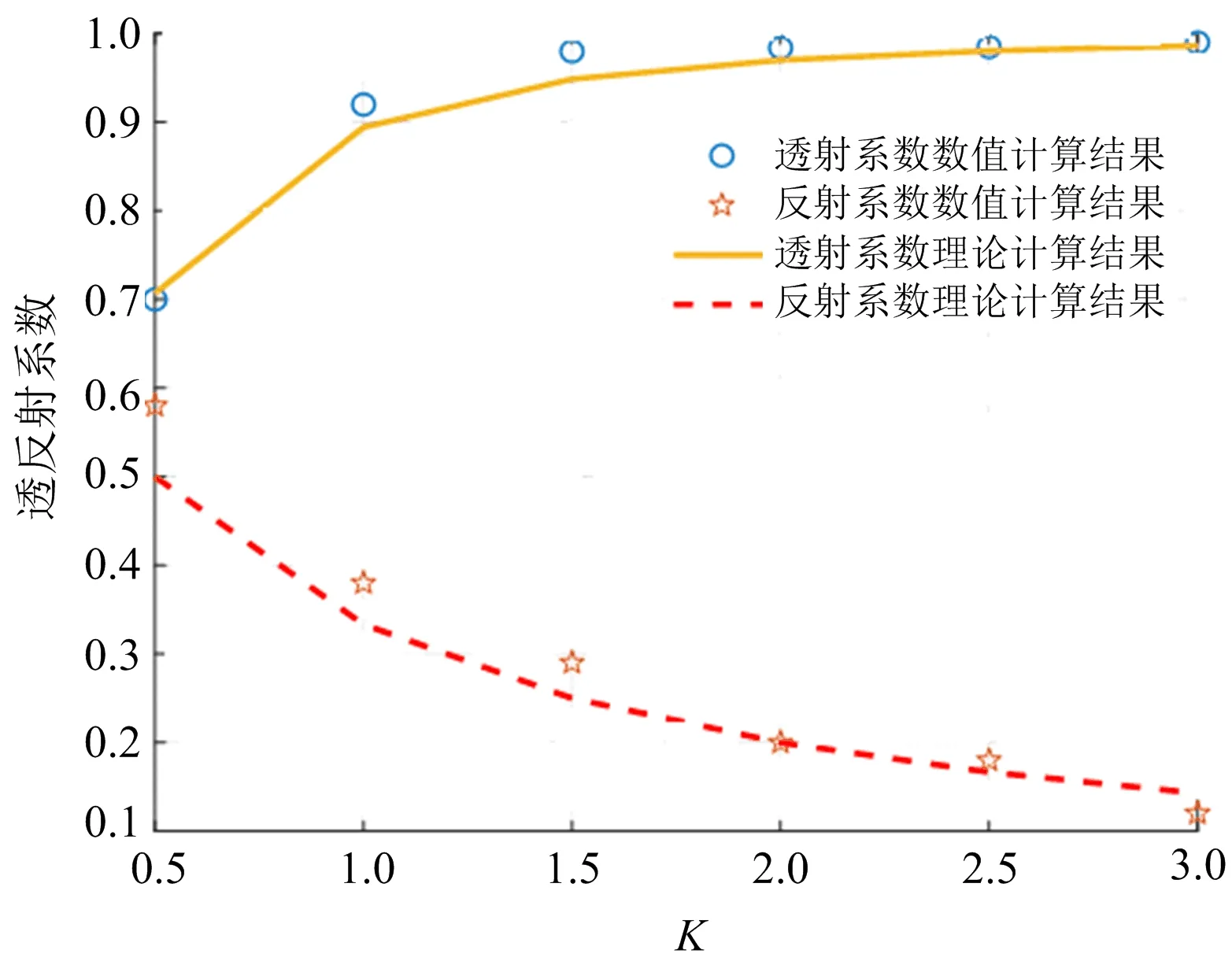
图4 不同节理刚度下透射系数和反射系数变化情况Fig.4 Variation of transmission coefficient and reflection coefficient under different joint stiffness

3 结果与讨论

由于在线弹性动力学中，各监测点质点振动速度线性地依赖于入射波的质点振动速度，即各监测点质点振动速度是入射波质点振动速度的线性齐次函数，因而研究各监测点质点振动速度与入射波质点振动速度的比值更具有一般性价值，为得出一般性的结论，需要定义如下参数：

质点振动速度放缩系数的定义为

(2)

式中：v(n)(t)为编号n点的振动速度；v(i)(t)为入射波的振动速度。

等效节理刚度的定义为

(3)

式中：Kn、Ks分别为节理法向、切向刚度；ω为入射波的角频率;Zp为波阻抗，且Zp=ρCp，ρ为岩体密度，Cp为岩体纵波波速。

3.1 节理刚度下SV波的传播规律

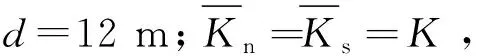
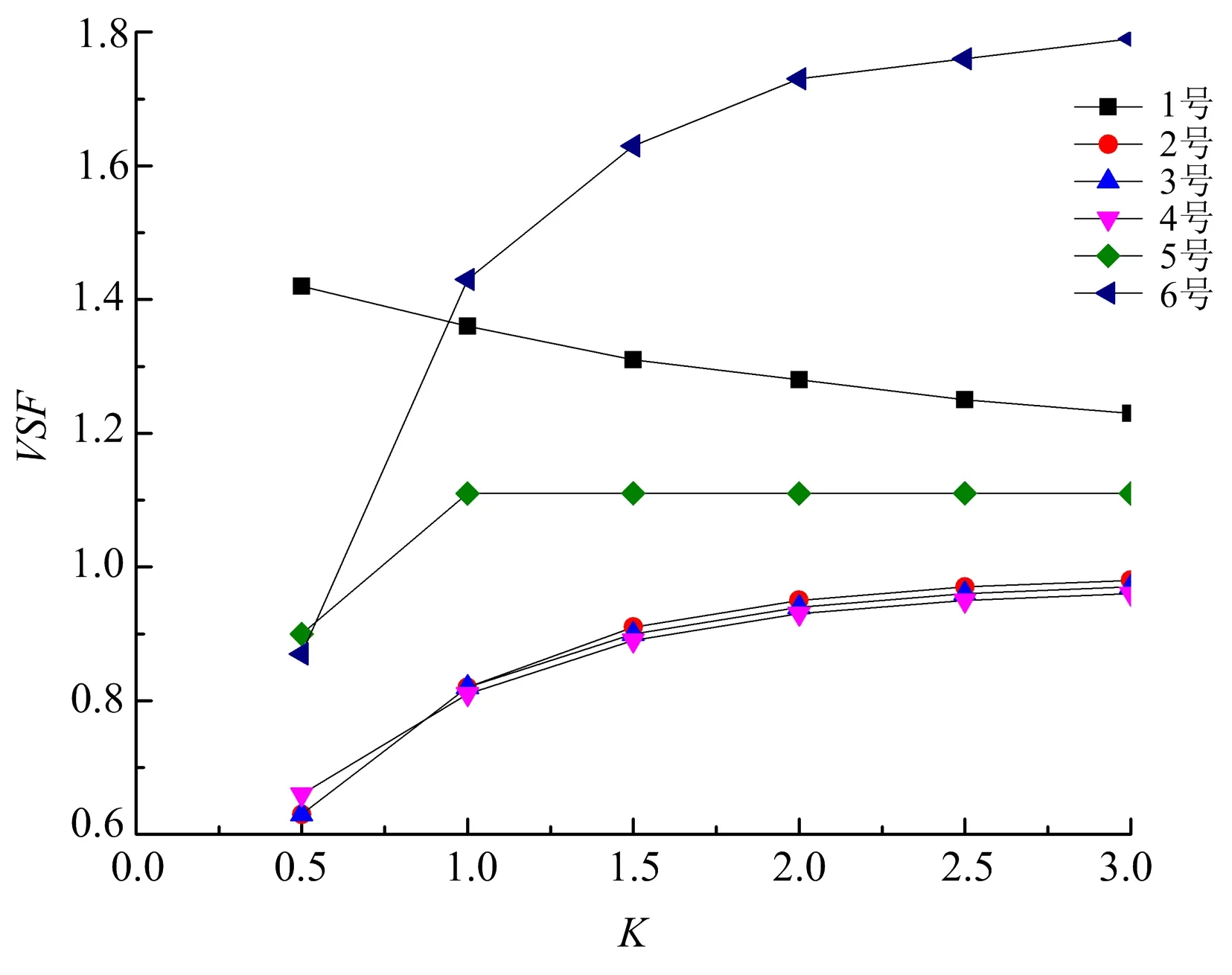
图5 各监测点VSF随节理刚度变化关系Fig.5 The relationship between the VSF of each monitring point and the joint stiffness

由图5可知，1号监测点的VSF随着等效节理刚度K的增大而逐渐减小，逐渐趋向1.2；2号、3号、4号监测点的VSF随着K的增大而增大，且其幅值及变化规律非常接近。在K相同的情况下，当K=0.5时，越靠近节理1，VSF越小，而当K增大时，VSF表现出相反的变化特性。5号监测点的VSF也随着K的增大而增大，但K>1.0时，VSF的值基本保持不变的。6号监测点的VSF也随着K的增大而增大，当K≤1.0时,VSF增大速度较快，当1.0≤K≤2.5时,VSF增大速度逐渐减小，当K>2.5时,VSF变化较小且趋向于1.8。

由以上分析可知，等效节理刚度K对不同位置的VSF的影响并不相同。总体来说，对节理1前的质点而言，VSF随K的增大而逐渐减小，而对于节理间以及节理2后的质点而言，VSF随K的增大而逐渐增大，但不同位置的VSF值及其增大速度并不相同。

3.2 节理倾角对SV波传播的影响

为了研究节理倾角对SV波传播的影响，选择相同节理刚度的条件来分析节理倾角对其产生的影响，因此取两种刚度K作为分析，其值分别取0.5和3.0。分别对两种刚度条件下的5种节理倾角进行分析(α取30°、40°、45°、50°、60°)。

各监测点的质点峰值振动速度放缩系数随节理倾角变化关系如图6～图7所示。

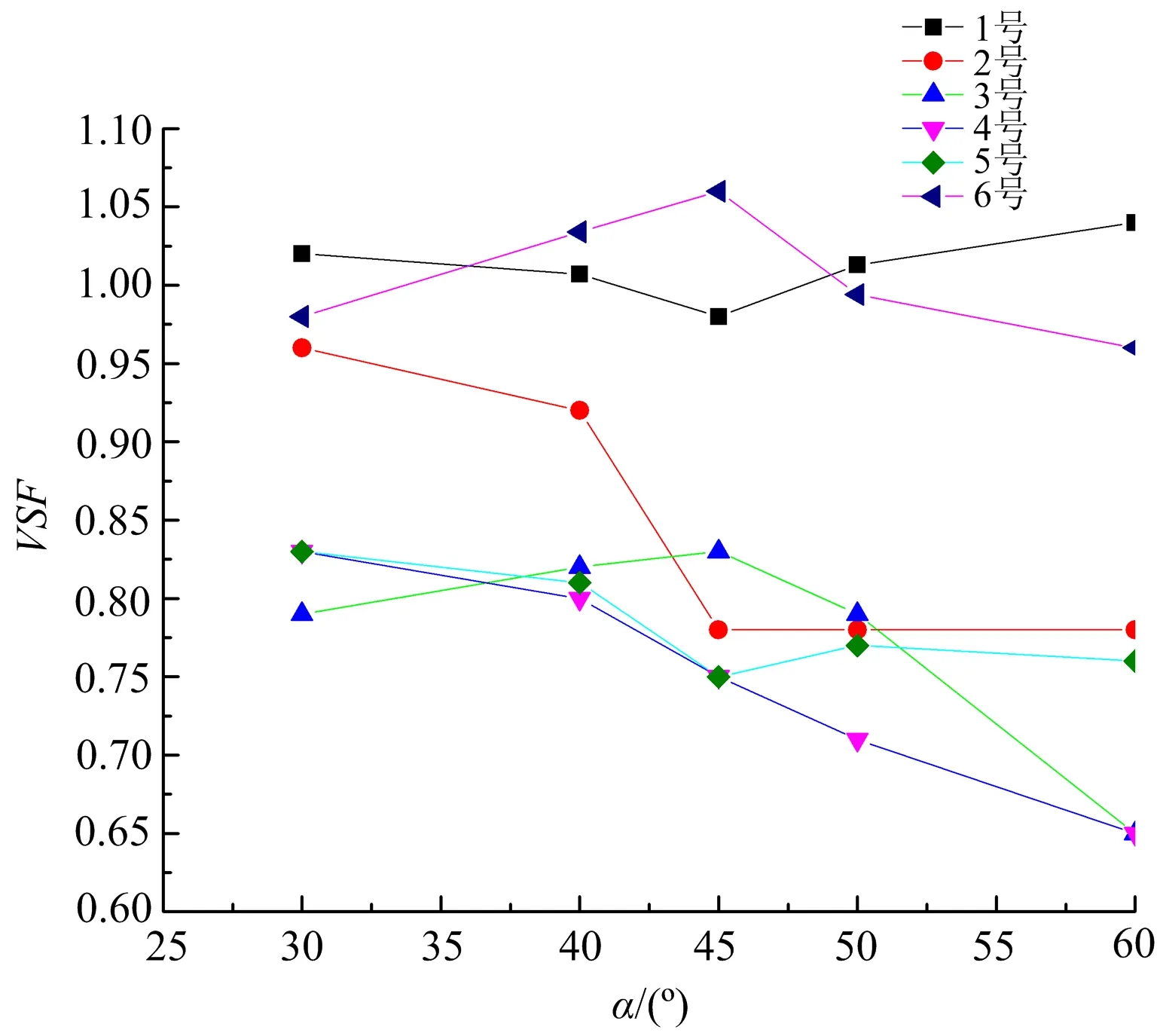
图6 各监测点VSF随节理倾角变化关系(K=0.5)Fig.6 The relationship between the VSF of each monitring point and the joint inclination(K=0.5)

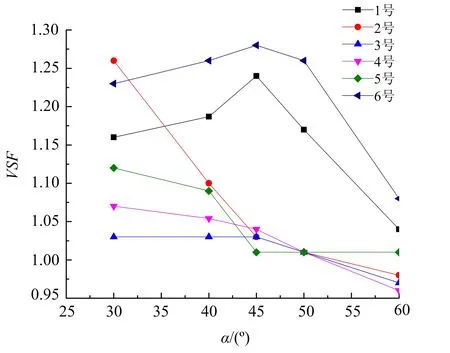
图7 各监测点VSF随节理倾角变化关系(K=3.0)Fig.7 The relationship between the VSF of each monitring point and the joint inclination(K=3.0)

在图6中可以看出，当K=0.5时，1、2、5号监测点的VSF随α增大的变化趋势为先减小再增大，45°时为拐点。3、6号监测点的VSF随α增大的变化趋势为先增大再减小，45°时为拐点。4号监测点的VSF则一直减小。

在图7中，可以看出当K=3.0时，1、3、6号VSF随α增大的变化趋势为先增大再减小，45°时为拐点。2、4号监测点一直减小。5号监测点的VSF随α增大的变化趋势为先减小再增大，45°时为拐点。

由以上分析可知，在相同等效节理刚度K下，节理倾角α对各个监测点的影响不同，对于不同等效节理刚度下，随着α的改变，各监测点的VSF变化也不同。

3.3 节理间距对SV传播的影响

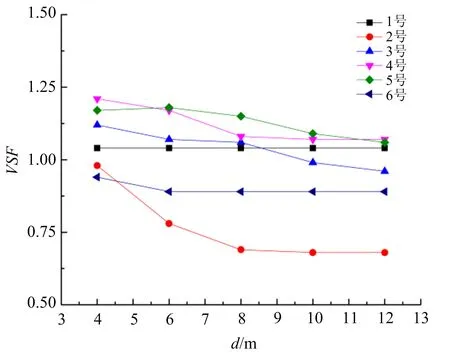
图8 各监测点VSF随节理间距变化关系(K=1.0)Fig.8 The relationship between the VSF of each monitoring point and the joint spacing (K=1.0)

由图8可知，随着节理间距d的增大，1号监测点的VSF保持不变，为一条水平直线，2～6号监测点随着d的增加，VSF随之减小。2号、6号监测点的VSF分别在d=6 m与d=8 m后趋于水平，其他3个监测点的VSF呈下降趋势。观察可以发现，d≥6 m时，在d值相同的条件下，在节理间的监测点越靠近节理1，则其VSF越小。

由此可知，1号监测点在两条节理之前，由于不同的节理间距是由节理2控制的，而节理1是不移动的，所以在节理1位置不变时，监测点与最近的节理距离保持不变的情况下，监测点处的VSF是始终保持不变的。分析图8中2～6号监测点折线可以发现VSF随着节理间距d的增大都有所下降，但其减小速度越来越平缓，这说明节理间距对SV波的传播有一定的影响，但当d大于某一值时，节理间距对SV波传播的影响会越来越小。

4 结论

1)在节理1前监测点的VSF随着等效节理刚度K的增大而逐渐减小。在节理间、节理2后的监测点的VSF随着K的增大而增大。

2)随着节理倾角的改变，不同位置的VSF表现出较为复杂的变化特性，但均在45°处出现拐点。

3)随着节理间距d的增大，VSF在一定范围内减小，大于这一范围时VSF趋于稳定。