爆炸焊接中覆板碰撞速度的确定

郭子如，张仲一，周佐玉，魏善太，何志伟，刘 锋，刘 伟，李洪伟

(1.安徽理工大学化学工程学院，安徽 淮南 232001；2.湖北金兰特种金属材料有限公司，湖北 赤壁 437300；3.江南化工股份有限公司，合肥 230022)

爆炸焊接是一种利用炸药爆炸所产生的能量为能源的一种焊接技术，这种技术在近些年得到了大力的发展和广泛的应用[1-3]。覆板与基板的焊接质量与覆板的碰撞速度密切相关，所有其他爆炸焊接的参数都是围绕这一关键因素展开的，而碰撞速度与很多因素相关，焊接工艺和炸药种类、爆炸性质、装药量、覆板的密度等都影响着碰撞速度。本文就此进行了讨论和分析，以期对爆炸焊接工程实践有借鉴作用。

1 覆板速度理论计算

1.1 格尼(Gurney)公式

爆炸载荷作用下覆板的运动问题其实是一个复杂的二维不定常的爆炸力学问题，属于爆轰驱动范畴。1943年格尼(Gurney)在研究时建立了一个一维膨胀模型下的近似公式[4]，即格尼(Gurney)公式，假定：①爆轰是瞬间完成的；②覆板瞬时就获得了极大速度；③爆轰产物质点流动速度在运动方向上是线性分布的。

在上述假设下，炸药爆轰释放的能量全部用于驱动覆板运动和爆轰产物获得的动能，于是可以推导出格尼公式：

(1)

式中：E0为格尼能；R为单位面积炸药与覆板的质量比。

1.2 阿述兹(Aziz)和特里巴斯(Deribas)的公式

阿述兹的研究模型假定[5]：①忽略覆板运动中空气阻力的影响，认为覆板在真空中运动；②只考虑爆炸载荷下覆板的刚体运动，忽略覆板本身的应变；③忽略侧向稀疏波对爆炸载荷的影响。在上述假设下再利用三大守恒定律可以推导出Aziz一维平板运动公式：

(2)

值得一提的是Aziz一维平板运动公式在推导过程中是假定炸药的多方指数γ=3的，其在γ=3时得到一维解析解，而在γ≠3则只能得到数值解。

1967年特里巴斯发现γ=2.5的炸药所驱动的平板运动速度约为γ=3炸药的1.22倍。由于在爆炸焊接中所使用的大量硝铵类炸药在密度为0.8 g/cm3左右时，γ=3，于是他建立了新的覆板运动公式[5]：

(3)

2 碰撞速度的影响因素及其上下限

影响基、覆板碰撞速度的因素并不是单一的，所用炸药的性能，布药厚度，覆板厚度和材质以及基、覆板间隙等都可以影响碰撞速度的大小。在炸药的性能方面，由式(1)～式(3)可以看出，炸药爆速是影响碰撞速度的重要因素。此外，炸药的密度也可以影响碰撞速度，一方面由于炸药密度影响炸药爆速，比如对于一般工业炸药其爆速都是先随密度增大到最大值然后逐渐减小到中断；另一方面是由于炸药密度的变化显著地影响炸药与覆板的质量比R。

炸药的装药尺寸大于临界值时炸药才可以稳定爆轰，而且当炸药的装药尺寸在大于临界尺寸小于极限尺寸的范围内时，其爆速会随着装药直径的增大而增大。文献[6]指出，在实际爆炸焊接时，民用炸药的爆轰都属于非理想爆轰，所以布药厚度也影响碰撞速度。

同样在其他条件确定时，考虑覆板厚度的影响。对格尼公式建立数学模型进行分析，发现碰撞速度vp的导函数在R>0时是单调递增的，又因为质量比R与覆板厚度d是呈反比的关系，所以碰撞速度vp关于覆板厚度d是单调递减的，也即d↑，R↓，vp↓。

对于基、覆板间隙距离，其大小选取不当的话会出现覆板加速距离过短导致覆板速度不足等情况。

基、覆板的碰撞速度实际上是各因素综合影响的结果，需要综合考虑并且使得各参数都位于“爆炸焊接窗口”之内，这样才能保证爆炸焊接的顺利完成。

爆炸焊接窗口主要是为了确定金属的可焊性参数范围，其主要参数是碰撞点移动速度vc以及覆板的碰撞速度vp。传统的爆炸焊接窗口如图1所示。

图1 爆炸焊接窗口Fig.1 Explosive welding window

1)碰撞速度下限。可以想象如果碰撞速度过低的话，那么覆板将不具备和基板良好焊接在一起的能量，所以碰撞速度vp应该具有一个临界值vp min，只有vp大于这个临界值时,才能使得两板的碰撞压力大于材料的屈服强度，这样才能使得两板结合处的金属产生射流进而获得比较好的焊接质量。单金属或两种相似金属爆炸焊接产生射流的最小碰撞速度为[7]

(4)

式中：σb为金属材料的极限抗拉强度，Pa；ρ为金属材料的密度，kg/m3。

由于维氏硬度HV与材料的极限抗拉强度成线性关系，所以式(4)可以变换为

(5)

式中：HV是维氏硬度；ρ为金属材料的密度；Kc为系数，一般取在0.6～1.2之间。

2)碰撞速度上限。如果碰撞速度过高的话，那么覆板必然是具备极大的动能，此时在两板结合处就会积累非常高的热量，卸载后的界面仍处于热软化状态，反射的卸载拉伸波就会将结合面拉开从而影响焊接质量[8]。所以碰撞速度vp也应该具有另一个临界值vp max，只有碰撞速度vp小于这个值时才会得到较好的焊接质量。文献[8]给出了碰撞速度上限的公式：

(6)

式中：Cp为比热；α为热扩散率；h为金属板材的厚度；ρ1和ρ2分别表示覆板与基板的密度；vc为碰撞点移动速度；N为上限理论系数，一般取0.039；Tmp min为双金属的最低熔点温度；tmin为反射拉伸波到达焊接界面的最短时间。

3 运动速度公式的推导

爆炸焊接中覆板碰撞速度的计算一直使用的是格尼公式等计算公式，为了给爆炸焊接中覆板碰撞速度的计算提供更多的理论计算方法，这里按照一定的物理模型自行推导了另外两种覆板碰撞速度的计算公式。

3.1 能量模型公式

假定：①装药的爆轰是瞬时的；②不考虑爆轰产物沿覆板表面平行方向的飞散；③爆轰产物的流动速度在覆板表面垂直方向上是近似地成线性分布的。

在这里，只考虑炸药爆炸的能量转化为覆板的动能和爆轰产物的动能。根据能量守恒定律，在上述的假设下：

EH=EC+ER

(7)

式中：EH为炸药爆炸的能量；EC为覆板的动能；ER为爆轰产物的动能。

1)覆板的动能EC。假设覆板获得的初速度为v0，覆板质量为M，则根据动能的计算公式覆板的动能EC为

(8)

2)爆轰产物的动能ER。对于平板装药，初始装药药高为h0，装药爆炸之后平板距原装药顶部的距离为h，爆轰产物的体积由V0增加到V，在h处爆轰产物的流动速度为v，装药的上表面积为S，模型如图2所示。

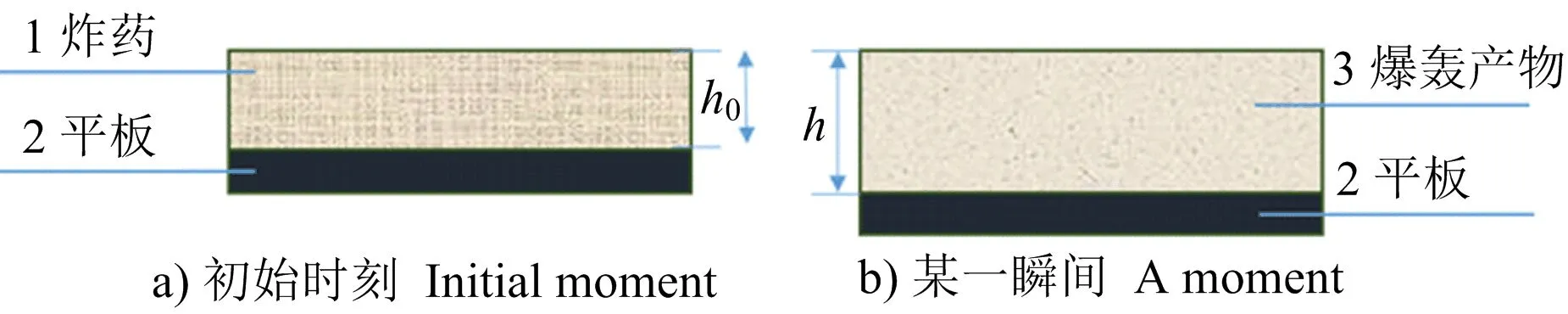
图2 平板装药膨胀过程Fig.2 Flat charge expansion process

由此可知：爆轰产物的动能表达式为

(9)

化简后得

(10)

欲积分式(10)则必须知道v的表达式，一般认为爆轰产物的流动速度v沿运动方向近似地成线性分布，同时认为紧贴在平板上表面的爆轰产物的流动速度等于平板的运动速度。由此可得

(11)

式中：hp为相当于覆板速度为v0时的膨胀半径(即距原布药顶端的距离)。

将v带入式(10)得

(12)

积分得

(13)

式中：m为炸药装药质量，实际上可以把m/3看作爆轰产物的虚拟质量m1，与此同时对于球形和圆柱形装药，爆轰产物的虚拟质量分别为3m/5和m/2[9]。

于是式(7)变换为

(14)

(15)

式中：QV为单位质量炸药爆热。

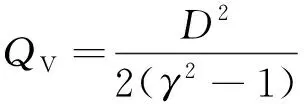
(16)

于是式(15)变换为

(17)

值得一提的是，式(16)是在理想爆轰的情况下才成立，而实际上爆炸焊接大多为非理想爆轰，所以式(17)的计算值会有一定的偏差。

3.2 动量模型公式

假定：①装药的爆轰是瞬时的；②爆炸能量用于平板的运动和爆轰产物本身的飞散；③爆轰产物的流动速度沿径向近似地成线性分布。如此，在某一瞬间平板与爆轰产物的运动方程为

(18)

式中：p为某瞬间爆轰产物的压力；S为平板在某瞬间受爆轰产物作用的表面积；v为平板在某瞬间的运动速度;M，m分别为覆板与炸药装药质量。

当平板运动到某h时，炸药爆炸作用于平板表面上的压力由pm降到p。对于平板装药，由质量守恒定律可得

hSρ=h0Sρ0

(19)

对于凝聚炸药：

(20)

将式(20)代入运动方程：

(21)

将两边同时积分处理后：

(22)

在爆炸焊接中，式(22)中的h可以认为是覆板与基板发生碰撞的位置，即h=h0+δ，δ为间隙距离。上面的4个碰撞速度计算式即式(2)、式(3)、式(17)、式(22)本质上与格尼公式是类似的，都可以表达为

v0=Df(R)

(23)

但是函数形式f(R)不同或者系数不同。

4 碰撞速度的计算与比较

段卫东等[10]利用双反射镜法测定了金属板材在不同质量比R下的运动速度，其实验所用炸药为2#岩石炸药，爆速为2 670 m/s。将实验条件带入能量模型和动量模型的公式进行计算，此处在动量模型的计算中可结合经验取h0=0.75h，计算结果用v1和v2表示，并与实测值以及格尼(Gurney)公式、Aziz公式和特里巴斯(Deribas)公式相比较，结果如表1所示。

爆轰产物的多方指数γ是描述爆炸焊接过程的重要参数，它随着炸药种类、密度、爆速以及基板和覆板安装方式的不同而变化。这里取γ=3计算。

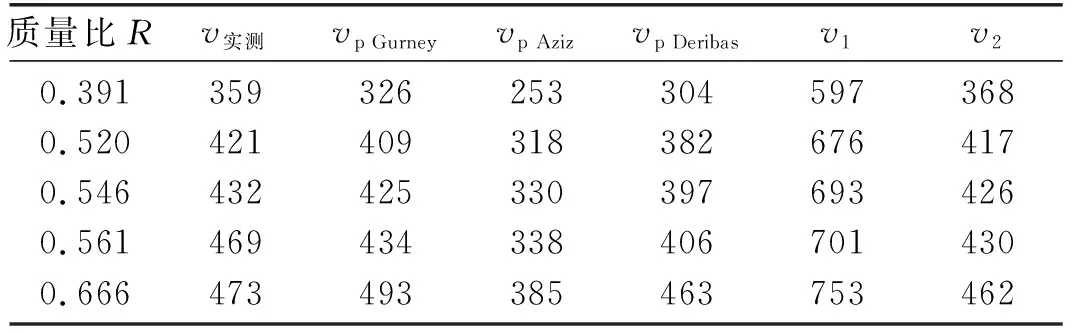
表1 不同质量比计算结果对比

从表1可以看出，能量模型的计算值稍稍偏大，动量模型的计算值与实测速度和几种文献中公式的计算值相当接近。

文献[11]介绍的选取低爆速乳化炸药进行不锈钢-钢爆炸焊接的实验，炸药爆速为2 092 m/s，质量比R=1.32，间隙距离δ=7 mm，覆板厚度3 mm，基板厚度18 mm，焊接质量良好。以此为场景一代入几种文献公式和新推导的公式进行计算，能量模型和动量模型的计算结果仍分别用v1和v2表示。

另外对于一维格尼公式中的格尼能，文献[12]给出了格尼能的计算式：

(24)

式中：γ为爆炸产物的多方指数，取2.8；D为炸药爆速。

文献[13]介绍的用加入添加剂的岩石硝铵炸药进行的铜-A3钢的爆炸焊接实验，爆速为2 048 m/s，炸药厚度23 mm，密度为0.841 g/cm3，δ=5.5 mm，覆板厚3 mm，基板厚5 mm，多方指数仍取2.8。以此为场景二计算得到铜-A3钢的各公式理论计算值。

文献[6]介绍的利用爆炸焊接法制作铝-钢电极，用的是粉状乳化炸药，药厚12 mm，爆速2 000 m/s，密度为1.0 g/cm3，δ=10 mm；覆板厚3 mm，基板厚度30 mm，多方指数仍取2.8。以此为场景三计算得到铝-钢的各公式理论计算值。以上各场景中的材料特性参数如表2所示。

表2 金属板材的材料特性参数

在上述条件下可以得到各公式的计算值并且根据式(4)、式(6)，分别计算得到爆炸焊接碰撞速度的上下限。不同种金属(双金属)的爆炸焊接下限计算不同于单金属或两种相似金属的计算，要先计算出单金属产生射流的最小碰撞速度，然后计算出单金属的最小可焊压力，取两者间较大者作为双金属焊接的最小可焊压力，再根据式(25)、式(26)：

(25)

(26)

式中：C0为材料声速；ρ为材料密度；λ为线性系数，对于铝，λ取1.34，对于钢，λ取0.454，对于铜，λ取1.51[14]，处理后得出双金属的碰撞速度下限为[15]

(27)

各公式的理论计算值和上下限计算值如表3所示。

表3 各公式理论计算值及上下限

从表3可以看到，在若干场景中动量模型的计算值v2与几种文献中公式的计算值非常接近，而能量模型的计算值v1稍微偏大，比v2平均高约35%；各公式的计算值都处在爆炸焊接上下限之间，且与上限有较大差别，各场景下v2分别是爆炸焊接上限值的44%、26%和47%，而与下限较为接近，是下限的1.76、1.21和1.30倍。

5 结论

1)基板与覆板的碰撞速度是决定爆炸焊接质量的关键因素，所有其他参数如炸药种类、爆炸性质、装药量、覆板的密度等都归结于碰撞速度。

2)本文推导的动量模型计算公式具有一定的准确性和实用性，与文献中的计算式有可比性，可用于指导爆炸焊接实践。

3)在爆炸焊接中要根据实际情况计算碰撞速度，并依据上下限公式计算出碰撞速度上下限，使得碰撞速度在上下限范围之内，以期得到良好的焊接质量。