整合DBSCAN和改进SMOTE的过采样算法

王 亮，冶继民

西安电子科技大学 数学与统计学院，西安 710126

1 引言

不平衡数据集是指数据集中某些类的样本个数明显小于其他类的数据集[1]。在二分类问题中，定义拥有较多样本数量的类别为负类，将样本数量少的类别称为正类[2]。目前，在实际应用中不平衡数据集的分类问题普遍存在，比如：银行欺诈检测[3]、文本分类[4]、医疗诊断[5]以及卫星图像中的溢油识别等[6]。在类不平衡数据集的分类问题中，由于少数类样本的误分代价更大，所以少数类样本比其他类别数据更重要[7]。传统分类算法对不平衡数据集中多数类样本的识别率较高，易忽略少数类样本，从而削弱分类器对少数类数据的预测能力，降低分类器的分类性能[8]。因此，如何有效地解决不平衡数据集的分类问题成为了数据挖掘领域中的重要研究内容。

数据集的不平衡状态可以细分为两种：类间不平衡和类内不平衡[9]。其中类间不平衡是指数据集中各个类别之间样本数量的不平衡，而类内不平衡是指在某一类样本空间内部数据分布密度的不均衡，即形成了多个具有相同类别、不同数据分布的子类[10]。

目前，解决不平衡数据集分类问题的方法主要分为两个方面：算法层面和数据层面[11-12]，前者对标准的分类算法进行改进，使分类器适应不平衡数据集下的分类[13]；后者则是对数据进行处理，减少数据集的不平衡程度，从而使分类器能够在平衡的数据集上进行学习[14]，其中最为常见的方法是数据层面的欠采样和过采样技术[15]。将多数类样本数量减少到与少数类样本数量大致相等的方法称为欠采样，例如：随机欠采样是随机删除多数类样本，以平衡数据集中不同类别样本的个数，但是，此方法容易丢失多数类样本中有价值的分类信息[16]。与欠采样相反，过采样技术是通过增加少数类样本的数量使数据集达到平衡的状态[17]。其中最具有代表性的过采样方法是Chawla 等人提出的SMOTE 算法[18]，SMOTE 在少数类样本和其相邻少数类邻居的连线上引入合成样本，通过人为构造新少数类样本从而消除原始数据集的类间不平衡度。但是，SMOTE 算法忽略了少数类样本类内不平衡现象的存在，并且易受噪声的影响，扩展少数类的分类区域。当不平衡度较高时，合成的新少数类样本点会与原始数据高度相似，甚至重复，很难为分类器提供新的分类信息。

基于SMOTE过采样算法，Han等人[19]提出了Borderline-SMOTE 算法，其核心思想是重点对位于分类边界的少数类样本进行过采样，加强对分类边界样本的学习以提高分类性能。He等人[20]提出的ADASYN算法根据数据分布自动确定每个少数类样本需要生成新样本的数量，拥有越多多数类邻居的少数类样本生成更多的新样本。相比于SMOTE算法，Borderline-SMOTE和ADASYN算法只对样本的分布进行了细致划分，因此依然存在SMOTE算法出现的问题。Douzas等人[21]提出了K-means SMOTE 算法，该算法首先使用K-means 算法对整体数据集聚类，然后仅在少数类样本数量大于多数类样本数量的簇中使用SMOTE过采样算法。该算法可以有效降低噪声的影响，抑制合成的少数类样本入侵多数类区域。然而，K-means SMOTE算法过滤了少数类样本数量占比小的簇，这些簇中包含的少数类样本极有可能位于分类边界，包含了大量有价值的分类信息，并且使用SMOTE 算法进行过采样，合成的少数类样本之间依然高度相似，甚至重复。

针对以上过采样算法存在的问题，本文提出了DB-MCSMOTE算法。首先，对少数类样本使用DBSCAN算法聚类，过滤噪声样本；其次，根据本文提出的簇密度分布函数，计算各个簇需要生成的样本数量；最后，在每个簇中使用改进的SMOTE算法（MCSMOTE）进行过采样，得到类间和类内均达到平衡的新数据集，并且合成的少数类样本具有多样性。

2 理论知识

2.1 SMOTE算法

SMOTE算法的基本思想是：根据采样倍率N%，在特征空间中通过对少数类样本点和其相邻的k个少数类邻居之间进行随机线性插值，从而合成新的少数类样本。具体步骤如下：

（1）根据欧式距离，使用KNN算法搜索每个少数类样本xi的k个近邻，记为：y1,y2,…,yk，其中k值的选取默认为5。

（2）在xi的k个少数类邻居中随机选择N个，并根据以下公式生成新样本xg：

其中，g=1,2,…,N,j=1,2,…,k，rand(0,1)表示0到1之间的随机数。

（3）将生成的新样本全部加入原始训练数据中，消除训练数据集的不平衡度。

2.2 DBSCAN算法

DBSCAN 是一种常用的密度聚类算法，它利用样本点的局部密度来划分簇，不需要提前设定簇的个数k，同一簇中的样本点是紧密相连的。假设数据集D={x1,x2,…,xm} ，给出如下关键定义[22]：

定义1（Eps-邻域） 对于xi∈D,xi的Eps-邻域包含数据集D中与xi的距离不大于Eps的数据点，即NEps(xi)={xj∈D|dist(xi,xj)≤Eps} 。

定义2（核心点）对于xi∈D，若xi的Eps-邻域中至少有MinPts个点，则称点xi为核心点。

定义3（直接密度可达）对于xi,xj∈D，若满足条件：xi是核心点，且xj∈NEps(xi)，则称xj可由xi直接密度可达。

定义4（密度可达）如果存在一系列的点y1,y2,…,yl，满足xi=y1，xj=yl，且yi+1是由yi直接密度可达的，则称xj可由xi密度可达。

定义5（密度相连）若存在样本点y，使得xi和xj均由y密度可达，则称xi和xj密度相连。

DBSCAN 算法将一系列密度相连的样本点的最大集合定义为一个聚类簇，不属于任何簇的一组样本点被定义为噪声集。不同于通常只适用凸样本集的K-means算法[23]，DBSCAN 算法不仅可以挖掘任意形状的簇，还可以有效过滤噪声点[24]。

3 整合DBSCAN和改进SMOTE的过采样算法

针对SMOTE等传统过采样算法存在的问题，如：忽略类内不平衡现象、合成的少数类样本意外入侵多数类样本区域以及合成高度相似的新样本，本文先将SMOTE 算法进行改进，并结合DBSCAN 聚类算法，提出了DB-MCSMOTE过采样算法。

3.1 簇密度分布函数和过采样权重

假设原始少数类样本集合经过DBSCAN算法聚类之后，得到m个簇：C1,C2,…,Cm。为了解决类内不平衡的问题，对于每个聚类簇Ci，本文定义了簇密度分布函数和过采样权重。

定义6（簇密度分布函数）簇Ci的密度分布函数定义为簇Ci中所包含样本点的个数与其所包含样本点构成的超球体体积的比例型函数。簇Ci的密度分布函数公式如下：

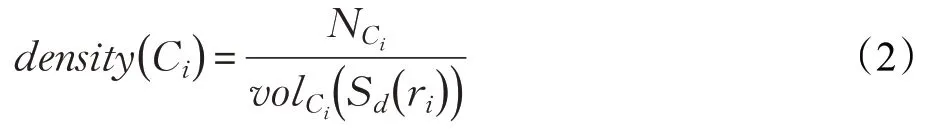
其中，NCi表示簇Ci中样本点的个数；volCi(Sd(ri))表示簇Ci中样本点构成的d维超球体的体积；ri表示簇Ci中离质心ui最远的样本点到质心ui的欧式距离；质心。簇Ci的密度分布函数值越大，代表簇Ci中的数据分布越密集。

定义7（过采样权重）簇Ci的过采样权重定义为其密度分布函数的倒数除以所有簇密度分布函数倒数的总和。簇Ci的过采样权重公式如下：

3.2 改进的SMOTE算法

本文提出了一种改进的SMOTE 过采样算法，即中点质心合成少数类过采样算法（MCSMOTE），其基本思想是：原始少数类样本集合经过DBSCAN 算法聚类后得到m个簇：C1,C2,…,Cm，在各个簇中选择相距较远的样本点进行两两配对，并在配对之后的样本点连线的中点处合成新样本，即公式（1）中rand(0,1)固定为0.5。随后不断地在合成样本和其相邻的父代样本点之间连线的中点处合成新子代样本，使合成的新样本不断靠近质心。具体步骤如算法1。

MCSMOTE算法具体的过采样过程如图1所示：分别从近质心集合Xmin和远质心集合Xmax中选择第一个样本点x1和xmid+1。第一轮中，MCSMOTE 算法在两个相距较远的样本点x1和xmid+1连线的中点处合成新样本。在第二轮中，MCSMOTE 算法分别在第一轮合成样本和其相邻的父代样本x1,xmid+1的连线中点处合成新样本，即在x1和xmid+1连线的四分位点处合成新样本。在第三轮中，MCSMOTE算法分别在第二轮合成样本和其相邻父代样本的连线中点处合成新样本，即在x1和xmid+1连线的八分位点处合成新样本。以此类推：在第n轮中，MCSMOTE 算法将在x1和xmid+1的连线上共生成2n-1 个分布均匀的新少数类样本。

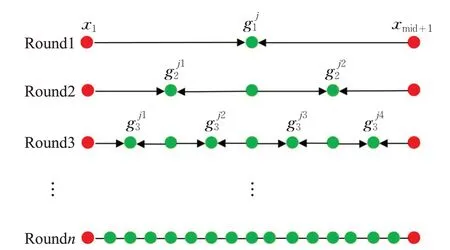
图1 MCSMOTE合成少数类样本示意图

3.3 DB-MCSMOTE算法

DB-MCSMOTE算法主要包括三个步骤：DBSCAN聚类、计算簇密度分布函数和采样权重、MCSMOTE 合成新少数类样本。具体步骤如算法2。

相比于SMOTE 等传统算法，DB-MCSMOTE 算法引入簇密度分布函数和采样权重的定义，因此该算法可以有效解决少数类样本类内不平衡的问题。其次，DB-MCSMOTE 算法过滤了噪声样本集并且在各个少数类簇中不断产生靠近该簇质心的新少数类样本点，有效克服了SMOTE 算法意外扩展少数类分类区域的弊端。最后，DB-MCSMOTE 算法没有使用KNN 算法搜索少数类样本的近邻，而是在两个相距较远的样本点的连线上不断合成新样本，因此可以提高合成少数类样本的多样性，避免生成高度相似，甚至重复的新少数类样本，为分类器提供更多有效的分类信息。

4 实验设计与结果分析

为了评估上述算法的性能，本文将UCI库中九个实际数据集和一个二维人工合成不平衡数据集作为实验数据集，将SMOTE、Borderline-SMOTE、ADASYN、K-means SMOTE 和 DB-MCSMOTE 五种过采样算法分别应用在实验数据集上，得到新的平衡数据集，并使用K近邻（KNN）、支持向量机（SVM）和随机森林（RF）进行分类，以评估每种过采样算法的性能。KNN、SVM和RF 算法已广泛应用于不平衡数据集的分类研究中[25-26]，其中RF 是一种经典的集成算法。RF 是由多个分类决策树组成的分类器，每一个基分类器中采用的独立同分布的随机向量决定了树的生长过程，最终通过多数投票机制来确定RF分类器的输出结果[27]。

4.1 数据集

（1）本文从UCI数据库中选取的九个实际数据集的详细信息如表1所示。在具有多个类别的数据集中，选择一类样本作为少数类，并将其他类别样本组合成多数类。其中Yeast-02579 是将Yeast 数据集中部分类别（ME1，EXC，POX）和（MIT，CYT，ME3，VAC，ERL）分别合并为少数类和多数类。在二分类问题中不平衡度IR的定义如下：

表1 数据集的基本信息

（2）为了更加直观阐明DB-MCSMOTE 算法的优势，本文使用人工合成的二维不平衡数据集，如图2 所示，不平衡度IR=3.2。该二维合成数据集不仅存在类间不平衡，并且在少数类类内也存在不平衡现象。与此同时，在该数据集的少数类样本中也存在着噪声。

4.2 评价指标

机器学习中的评价指标都是建立在混淆矩阵（见表2）上，其中：TP和TN分别代表正确分类的正类（少数类）和负类（多数类）样本数量，FP和FN分别代表错误分类的负类和正类样本数量。

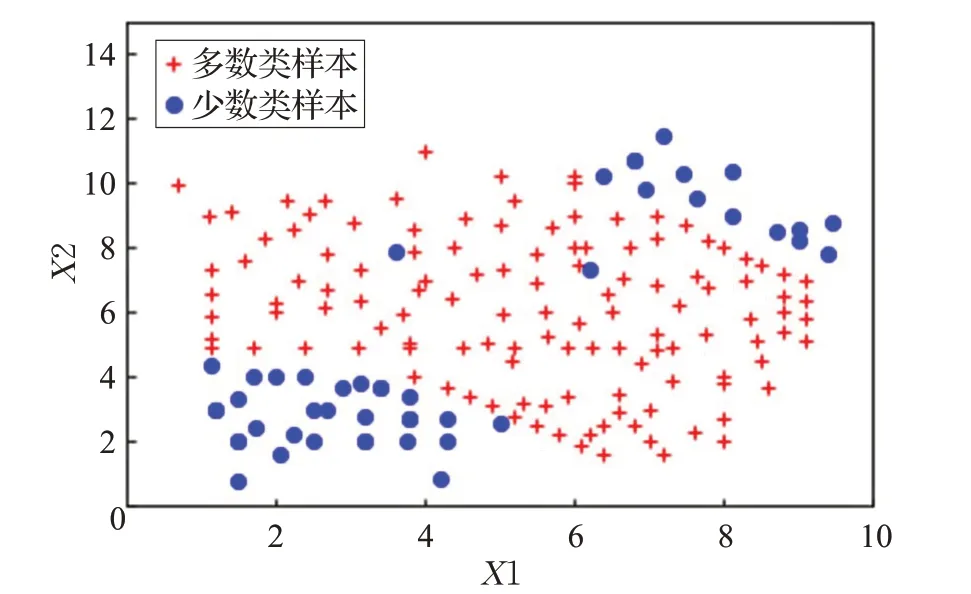
图2 二维合成数据集

表2 混淆矩阵

由于不平衡学习旨在提高少数类样本的分类性能，所以在评估分类性能的各种传统评价指标中，当类分布不均匀时，并非所有评估指标都适用，目前已有一些评估指标被专门用在不平衡数据集的分类问题中。本文选择F-value，G-mean和AUC三个评价指标来评估分类器的性能，其中AUC表示ROC曲线下各部分的面积之和，它表示分类器将随机测试的正实例排序高于随机测试的负实例的概率。F-value和G-mean的定义如下：

4.3 实验环境设置

本文使用Python语言，Spyder集成开发环境对各种算法进行仿真实验。根据原文献，将SMOTE、Borderline-SMOTE、ADASYN算法的近邻数k取值为5，Borderline-SMOTE 算法的参数m设置为10。K-means SMOTE算法参数k和knn的取值范围分别为k∈{2,20,50,100,250,500} 、knn∈{3,5,20} 。DB-MCSMOTE算法的参数Eps,MinPts通过k-距离曲线（k-dist graph）确定[22]。KNN算法近邻数k的取值为k∈{3,5,8} 。SVM算法中核函数选择高斯径向基函数（RBF kernel），惩罚因子C和核函数参数gamma取值范围为C∈{20,21,…,210},gamma∈{1 0-5,10-4,…,102} 。RF 算法中决策树的数量N_tree的取值范围为N_tree∈{1 0,50,100,200,500,800} 。为了获得所有分类器和过采样器的最佳结果，利用网格搜索算法确定最优参数组合。实验中使用十次十折（10-fold）交叉验证的平均值作为最终性能度量的结果。

4.4 实验结果与分析

（1）合成数据集实验结果：本文分别利用SMOTE、K-means SMOTE 和 DB-MCSMOTE 三种算法对二维合成数据集进行过采样，实验结果如图3、图4和图5所示。通过对比实验结果，得到如下结论：①在使用SMOTE 算法之后，降低了数据集的类间不平衡度。但是由于原始少数类样本中存在噪声，新合成的少数类样本意外入侵多数类样本区域，进一步放大了数据中的噪声，并且新生成的样本之间高度相似，甚至与原始少数类样本重叠。②K-means SMOTE 算法有效过滤了噪声，抑制了SMOTE 算法意外扩展少数类样本分类区域的现象。但是新合成的少数类样本之间依然高度相似，甚至重复。③DB-MCSMOTE 算法不仅克服了类间不平衡现象，也有效解决了少数类样本类内不平衡的现象。并且该算法不仅能避免新生成的少数类样本入侵多数类样本区域，降低噪声的影响，而且合成的新样本具有多样性，为分类器提供了更多的分类信息。

图3 SMOTE过采样结果

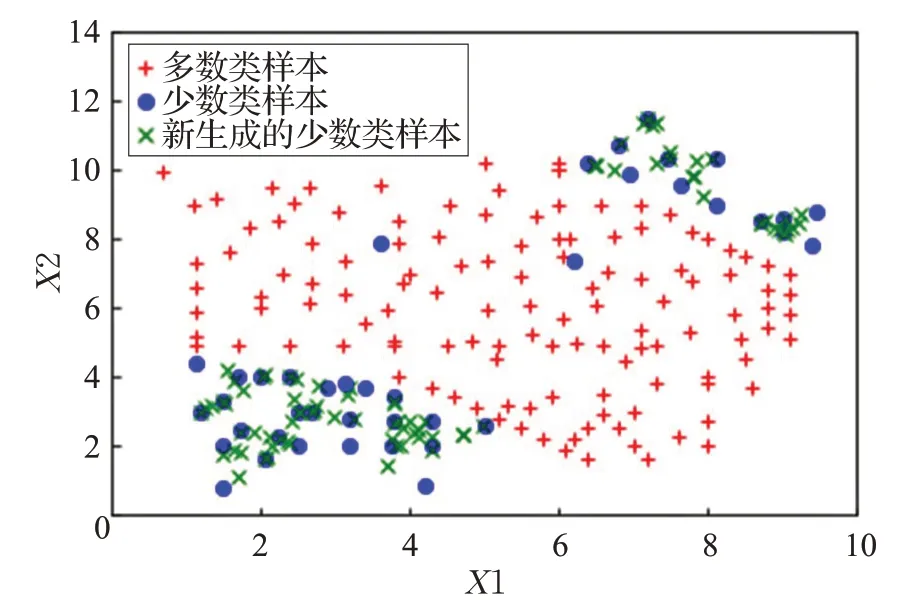
图4 K-means SMOTE过采样结果

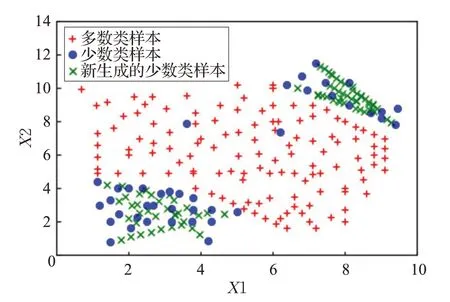
图5 DB-MCSMOTE过采样结果

（2）实际数据集实验结果：本文使用KNN、SVM 和RF分类器对原始数据集和经过采样之后的平衡数据集进行分类，实验结果见表3、表4 和表5，其中F-value、G-mean和AUC取得最优值的数据用黑色粗体表示。对于每个数据集中的每个评价指标通过得分制来对各种算法进行排序，分值设置为1到6，其中性能最好的算法得6 分，最差的得1 分。针对未经过采样和五种过采样算法，对于每个数据集中的三种评价指标的平均得分再取均值，可以得到每种算法的最终平均得分。通过对比实验结果可以得出如下结论：①在相同的数据集中，使用RF分类器可以获得优于KNN和SVM分类器的分类效果，这是因为RF 分类器将多个单一的弱分类器集合成一个强分类器，并且由于“随机性”的引入，使得RF分类器不易过拟合，同时具有较强的抗噪声能力。②相比于只对原始数据集使用KNN、SVM 和RF 分类器进行分类，使用SMOTE、Borderline-SMOTE、ADASYN、K-means SMOTE 和 DB-MCSMOTE 过采样算法可以不同程度地提高分类器对数据集的分类性能。并且相比于SMOTE 等传统过采样算法，使用DB-MCSMOTE算法可更大幅度提升分类器的分类性能，即DB-MCSMOTE算法可以获得最高的最终平均得分。因此DB-MCSMOTE算法不仅可以提高KNN 等单一分类器的性能，同时也可以提升RF 集成分类器对不平衡数据集的分类效果。③ 在Pima、Segment、Vehicle、Yeast1和Yeast-02579五个数据集中，使用DB-MCSMOTE算法可以同时取得最优的F-value值、G-mean值和AUC值，这是因为上述实际数据集不仅存在类间不平衡，并且在少数类类内也存在样本分布的不均衡，SMOTE 等传统过采样算法未考虑少数类类内样本的分布情况。④在所有数据集中，使用DB-MCSMOTE 算法在Yeast-02579 数据集上取得的F-value值和G-mean值相比于SMOTE 等算法的提升幅度最大，这是因为Yeast-02579 数据集的不平衡度最高，需要合成更多新少数类样本，SMOTE等算法合成的新样本之间高度相似，而DB-MCSMOTE算法合成具有多样性的新少数类样本，可以为分类器提供更多的分类信息。以上结果总体来看，本文提出的DBMCSMOTE 过采样算法可以有效提升分类器对少数类样本和整体数据集的分类性能。

表3 KNN分类器实验结果对比

表4 SVM分类器实验结果对比

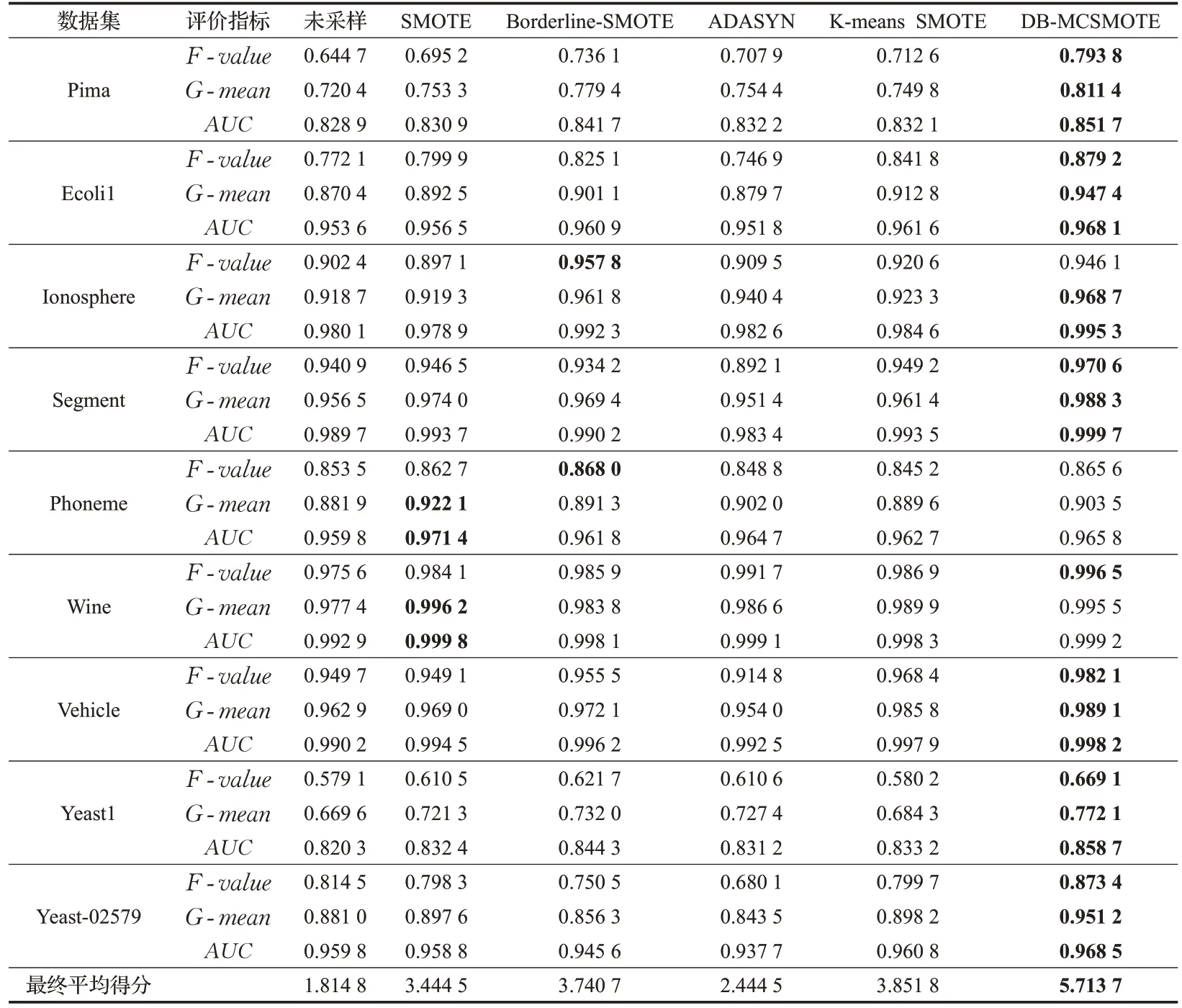
表5 RF分类器实验结果对比

5 结束语

不平衡数据集的分类问题广泛存在于实际应用中，对训练数据中的少数类样本进行过采样是一种有效的解决方法。本文对SMOTE算法进行改进，并结合DBSCAN聚类算法，提出了DB-MCSMOTE过采样算法。该算法首先使用DBSCAN 算法对少数类样本聚类，过滤数据集中的噪声；其次，通过本文提出的簇密度分布函数计算各个簇的采样权重，确定每个簇中合成新样本的数量；最后，使用改进的SMOTE过采样算法（MCSMOTE）合成新少数类样本。实验结果表明，DB-MCSMOTE算法可以有效克服SMOTE等传统过采样算法存在忽略类内不平衡、合成少数类样本入侵多数类区域以及合成样本高度相似等问题，并且可以有效提高分类器对少数类样本和整体数据集的分类性能。如何利用聚类算法将数据集进一步细分为噪声样本、边界样本和安全区样本，并重点对边界样本进行过采样是未来需要进一步研究的方向。