高精度钢轨扭曲度检测算法研究与应用

包亚俊，刘 瑾，杨海马，江声华，袁宝龙，杨 萍

(1.上海工程技术大学电子电气工程学院，上海 201620；2.上海理工大学光电信息与计算机工程学院，上海 200093；3.上海瑞纽机械股份有限公司，上海 200120；4.上海淮科智能科技有限公司，上海 201999；5.上海航天设备制造总厂有限公司，上海 200245)

0 引言

钢轨扭曲度[1]是指钢轨纵向的扭曲程度，它是判断钢轨质量是否合格的重要指标之一。目前，国内研究钢轨检测的比较少，依然是采用电子扭曲尺测量钢轨扭曲度，但在测量过程中需要两人共同操作才能完成，每次测量前都要对扭曲尺进行水平校准，该方法劳动强度大，耗费时间长，无法满足当前铁路高速发展[2]的需要。

文献[3-4]实现了钢轨扭曲度自动化检测，但在噪音较大的焊轨厂，该检测系统的测量精度波动较大，不能适应焊轨厂的环境；文献并没有对异常点进行处理，这些异常点与普通噪声偏差较大，严重影响滤波算法的精度，而且滤波算法效果并不明显。本文研究了一种基于激光轮廓仪非接触式[5-6]钢轨扭曲度自动检测系统，利用激光轮廓仪[7]采集到的钢轨廓形数据，比对扭曲尺测量方法，采用共面法建模求解。由于测量环境的变化、钢轨表面存在的毛刺、钢轨运动过程中的振动都会对测量点产生噪声误差，严重影响了测量数据的准确度，甚至影响了钢轨是否合格的误判。因此，本文将拉依达准则自适应阈值法与弦高差法相结合剔除异常点，选择更优的双正交小波算法对不同层次的阈值进行选择，有效地去除了因为灯光、钢轨运动过程中振动等噪声的干扰。最后，根据钢轨实际测量情况，改进残差，通过对比最小二乘法和最小绝对残差法的拟合情况，使用最小绝对残差法对数据进行线性拟合[8]，保证了系统的重复精度和准确精度。本系统具有自动化程度高、检测速度快、精度高等优势。

1 系统构成

本系统主要分为2个部分，分别是输送部分和检测部分。其中，输送部分主要分为前送轨和后送轨。前送轨和后送轨主要是将百米长的钢轨自轨头到轨尾输送至检测中心并将钢轨对中。前送轨用于在钢轨从辊道线进入时将钢轨夹紧，并且提供向前的动力。后送轨是在钢轨检测过程中对输出测量区域的钢轨提供夹紧对中，为测量提供稳定的条件。激光轮廓仪的布置方案如图1所示。

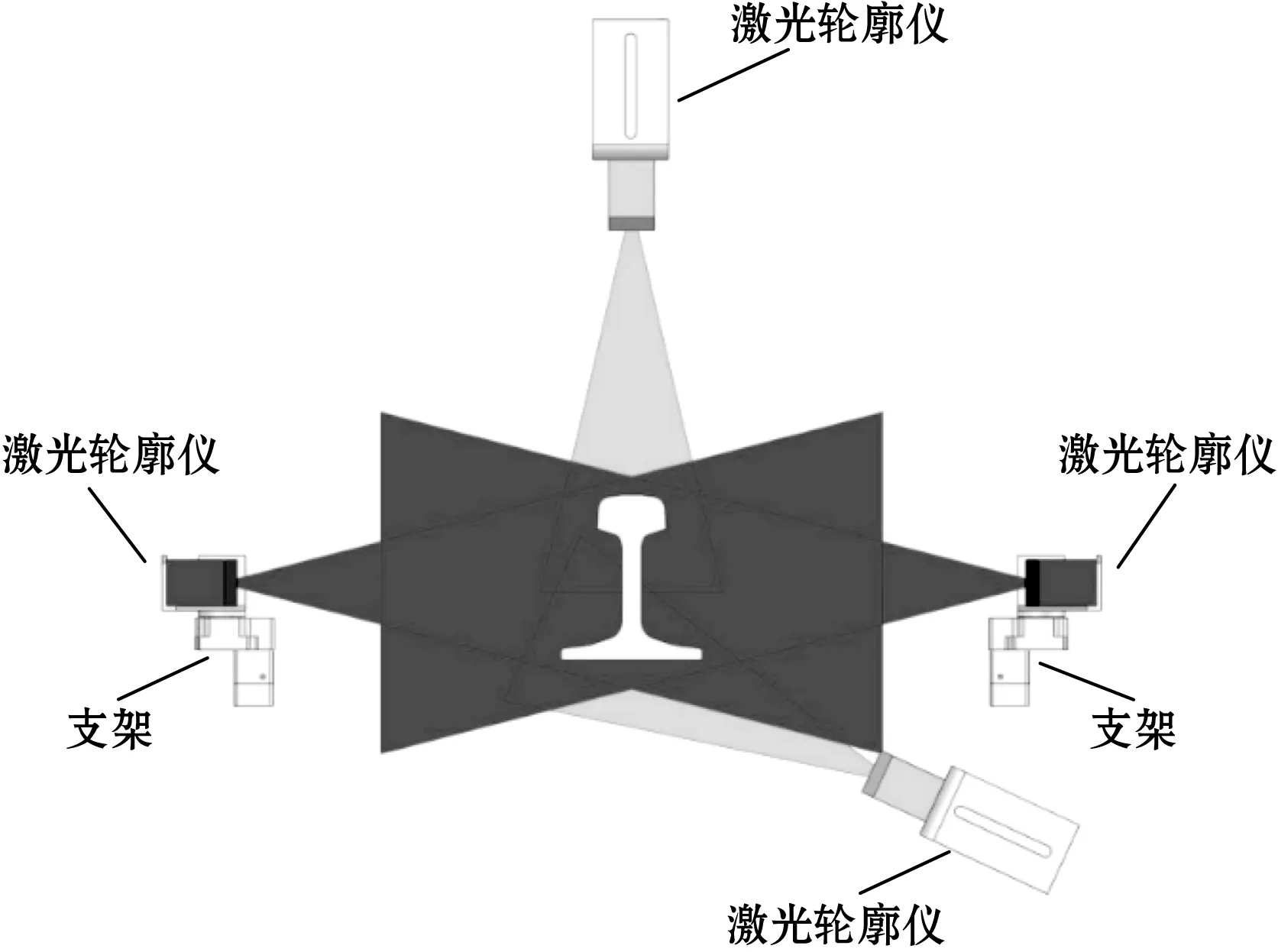
图1 激光轮廓仪扫描示意图

前送轨机构把钢轨输送到静态检测区域后停止输送，然后检测平台对轨端3 m进行静态测量。激光轮廓仪采集到的数据会实时通过以太网传送到工控机中。然后通过上位机软件对数据分析处理，最终得到静态参数的检测值，并在屏幕上显示。

静态检测结束后，前送轨机构继续控制钢轨以高速匀速前行，检测平台进行动态测量。此时，检测平台保持静止，激光轮廓仪采集钢轨廓形[9]数据。同时，在上位机对采集的数据进行处理后显示检测的各参数值。动态检测结束后，后送机构继续将轨尾送至指定位置，然后对轨尾3 m进行静态检测。全部检测完成后，后送轨机构将钢轨移出检测中心。

2 扭曲度模型设计

根据TB/T 3276—2011[10]的要求，用电子扭曲尺采集钢轨轨端1 m内的钢轨信息，其扭曲度不超过0.45 mm。触点中心与轨底边缘的距离为10 mm，触点接触表面为150～250 mm2。如图2所示，为钢轨端部扭曲尺测量示意图，其工作原理是固定好A、B、C3个触点，通过移动触点D(电子卡尺)直至与钢轨接触，电子卡尺的读数即为钢轨扭曲度值。

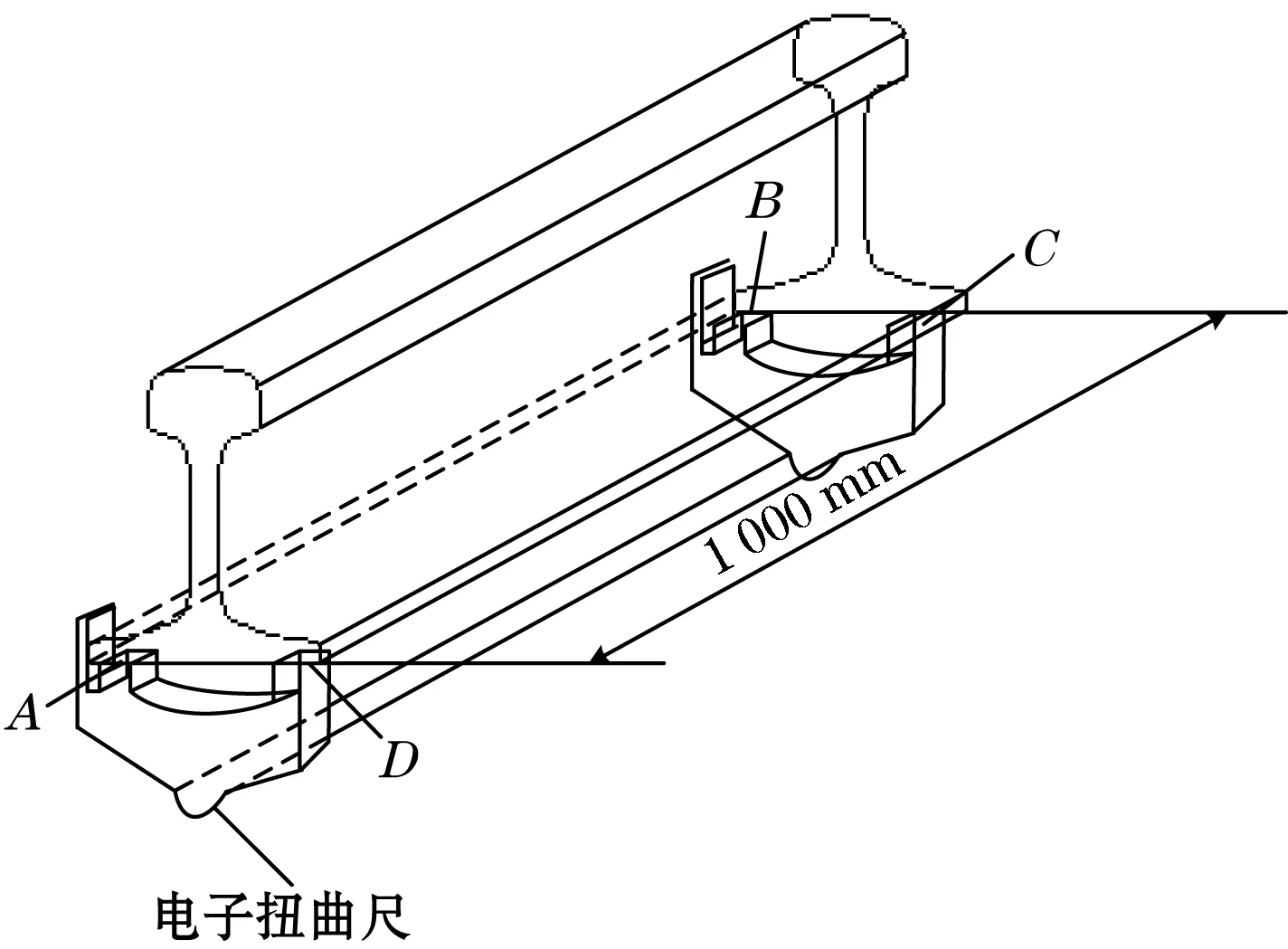
图2 端部扭曲测量示意图

根据电子扭曲尺的测量方式，本文采用共面法模型对扭曲度进行求解计算。传感器测得的数据是二维平面，共面法需要三维空间计算，因此本文将检测平台移动方向定义为z轴方向。图3是共面法模型，求出A、B、C3点所在的平面S，则D点到S平面的距离L即为所求的扭曲度。

图3 共面法模型图

具体实现方法如下：

(1)根据要求，在距离轨底边缘10 mm处分别取A、D两点。激光轮廓仪所获取的每帧数据上的点与点间距是0.2 mm，因此分别在第50个点和第700个点处取A、D两点；

(2)根据要求，扭曲尺采集的是钢轨1 m内的钢轨信息。每隔4 mm激光轮廓仪获取钢轨廓形一帧数据，因此在第251帧上取B、C两点；

(3)在实际测试中，钢轨表面会有残余的铁屑，直接影响激光轮廓仪的测量，因此，分别在4个触点附近取20点求其均值作为各自的点；

(4)根据建立的模型，利用三点共面原理，求出A、B、C3点所在的平面方程S；

(5)利用点到平面的公式求出D点到平面S的距离L，L即为扭曲度。

假设，平面方程S：ax+by+cz+d=0，A、B、C3点的坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)，根据克莱姆法则可以得到平面S的系数表达式：

(1)

则点D(x0,y0,z0)到平面S的距离L为

(2)

3 数据预处理优化

3.1 剔除异常点

根据现场情况，焊轨厂测量环境经常会有突然的变化，导致在测量数据时会出现异常点，与普通噪声产生的数据误差相比，异常点数据一般偏差较大。由于激光轮廓仪采集的点比较密集，因此，本文采用基于自适应阈值的弦高差法对异常点剔除。

图4为弦高差法，将检测点Pn前后两点Pn-1和Pn+1连接，然后计算点Pn到连接线的距离en，如果‖en‖≥[ε]([ε]为给定的允许偏差)，则Pn为噪声点剔除。

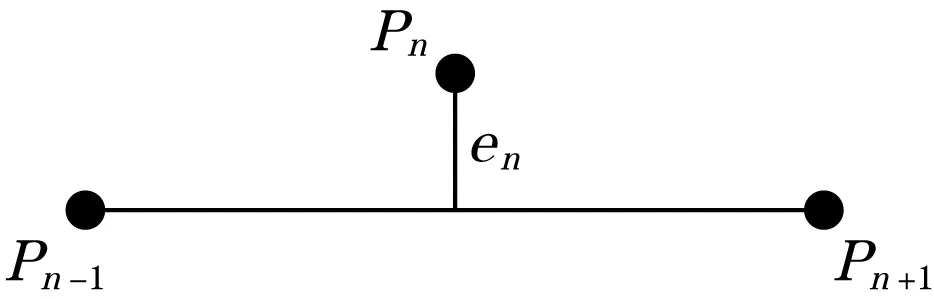
图4 弦高差法

在采用弦高差法剔除的过程中，阈值设置是否合适决定了数据处理的真实性，因此，本文采用拉依达准则(3σ准则)自适应阈值。假设变量x服从正态分布：

(3)

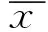
表1为数值概率表。由表1可以看出，变量x几乎全部集中在[-3σ,+3σ]区间内，概率达到99.73%，钢轨底部轮廓800个点，797个点在区间内。当阈值满足ρ=en+3σ，有2个异常点会被剔除。

表1 数值分布概率表

3.2 数据滤波

剔除异常点后的普通噪声点仍然影响着数据的真实性，无法达到钢轨检测的精度要求，需要对不明显的噪声进行平滑处理。由于离散小波变换最后是由两通道滤波器组来实现的，正交小波[11-12]都不具有线性相位(Haar小波除外)。因此，本文在小波降噪[13]的基础上，采用双正交小波法[14-15]对数据进行去噪处理。

(4)

式中：aj+1,k为离散逼近系数；dj+1,k为离散细节系数；n为采样点个数；j、k为采样点。

图5为分解算法图。

图5 分解算法图

(5)

在小波去噪方法中，噪声多存在于细节系数部分，因此，噪声去除关键是细节系数的处理，阈值的选取决定着算法的性能。小波降噪流程如图6所示。对于小波分解后的细节信号(高频区域)可以选择不同的阈值进行滤波。

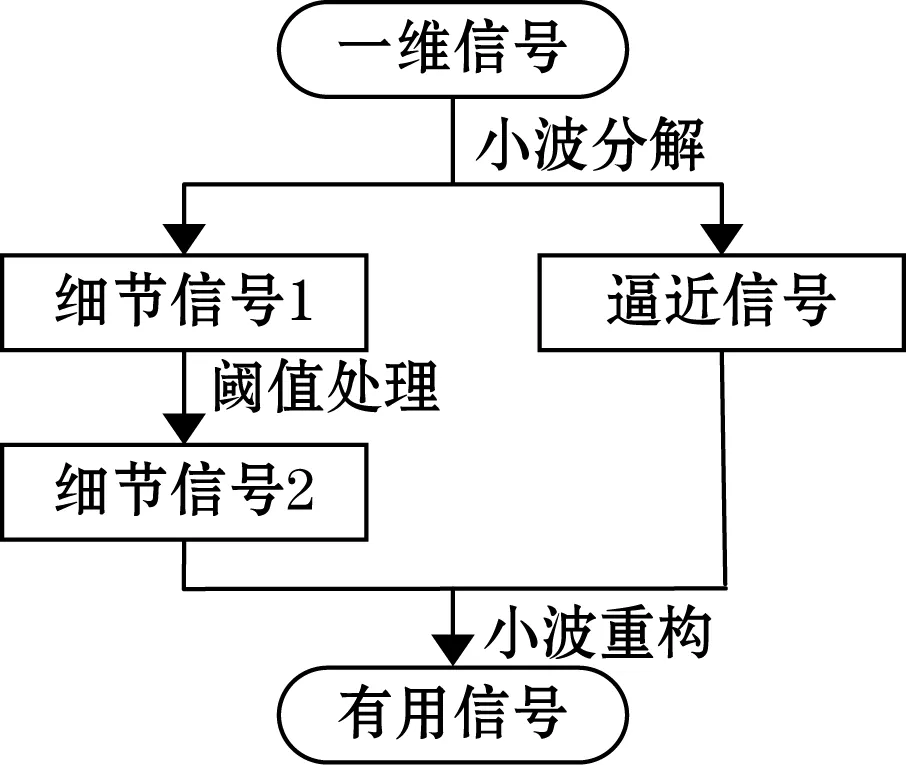
图6 降噪流程图

由于软阈值法中阈值连续性比较好，处理效果较为平滑，而硬阈值法重构小波时会出现失真现象。软阈值法公式为：

(6)

(7)

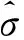
用双正交滤波器组(简称bior Nr,Nd，其中Nr是低通重建滤波器阶次，Nd是低通分解滤波器阶次)试验，本文拟取Nr为6，Nd为8。均方根误差(RMSE)是判断滤波性能的一项重要指标。结果如表2所示。

表2 不同滤波方法结果比较

由表2可以看出，双正交小波能够较好降低噪声对钢轨廓形数据的影响，处理效果较平滑，更有利于数据后续处理，图7为滤波前后效果图。

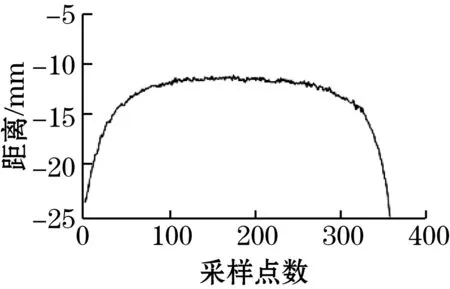
3.3 曲线拟合

经现场测试，发现滤波的数据已经得到了较好的去噪效果，但是在数据精度要求上会还出现不满足的情况。因此，根据钢轨扭曲度模型，本文采用线性拟合。在基于最小二乘法和最小绝对残差法拟合的基础上，改进它们的残差定义，拟合出更加符合钢轨扭曲度测量的直线。

3.3.1 最小二乘法拟合

假设自变量x和因变量y的函数关系由下列理论公式给出：

y=f(x;c1,c2,…，cn)

(8)

式中:c1,c2,…,cn为要通过n组数据确定的常数。

对于等精度测量所得到的n组数据(xi,yi)，其中i=1,2,…,n，xi值被认为是准确的，所有的误差只与yi相关。假设，x和y之间的函数关系最佳表达形式为

(9)

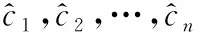
如果实际观测数据与理论模型之间不存在误差，那么n组数据都应该落在曲线y上。但是在实际测量过程中，实际观测数据并不能够完全与理论直线拟合而存在误差，因此实际值与拟合值会存在一个误差，这个误差叫做残差ei，则有：

(10)

在n对实际观测数据中，有多数点(xi,yi)落在曲线y上，那么曲线y就可以比较准确地反映实际观测数据的关系。显然，有多少数据就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性。当观测点落在曲线上的概率最大时，且观测误差服从正态分布，则概率为

(11)

当式(11)概率达到最大值时，可以得到最佳曲线。当式(12)取最小值时，可以得到最优解：

(12)

通过对式(12)求导，当导数为0时，可得到最小值，这种方法为最小二乘法。

根据实际检测，钢轨表面是平面，激光轮廓仪获取的数据符合直线模型，因此本文选择最小二乘法线性拟合。假设x和y之间的函数关系可以用式(13)直线方程模型表示：

y=ax+b

(13)

式中:a、b为2个待定常数。

对于任意实际观察点(xi,yi)带入可得：

(14)

对式中的a，b分别求一阶偏导数就可以得出a和b的值。针对钢轨取点实际情况，钢轨表面取点数接近800个点，为了减小偏差，本文对式(14)改进，可以依据下列等式最小化残差，得到对线性模型的斜率和截距：

(15)

式中：wi为第i个观测点的权重，根据实际测量，本文权重取1。

3.3.2 最小绝对残差法拟合

利用最小二乘法拟合直线求解并不令人满意，参数的收敛值和真实值相差较大，导致求得的扭曲度无法满足要求。根据这一问题，本文利用最小绝对残差法对观测点进行直线拟合。改进后的残差指标为

(16)

当式(16)残差取最小值时求出的斜率和截距称最小绝对残差解。在未知随机噪声的统计特性时，用最小绝对残差法效果会比最小二乘法好。最小绝对残差法对奇异点不太敏感，鲁棒性好。图8是分别使用最小二乘法和最小绝对残差法的线性拟合图。

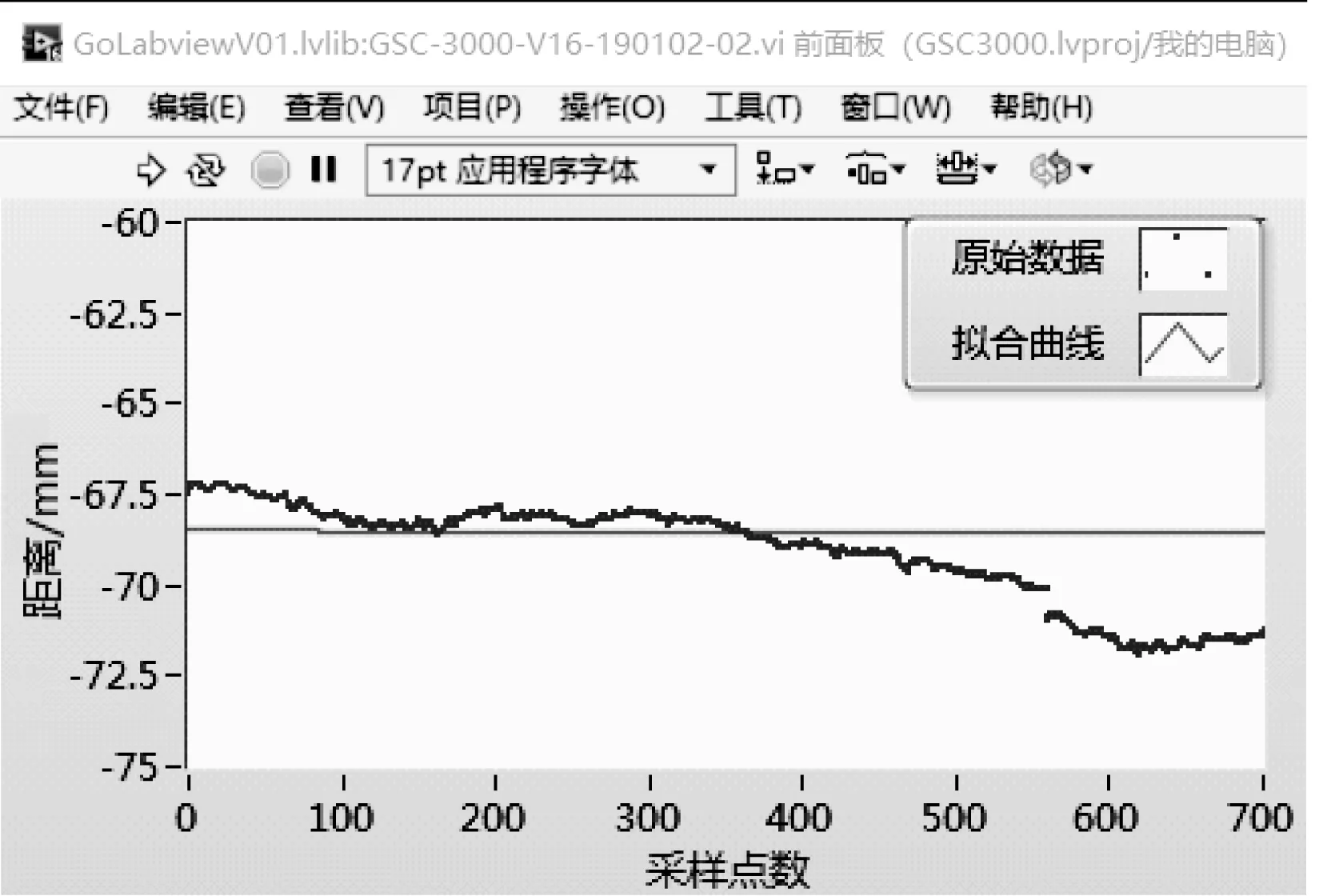
(a)最小二乘法

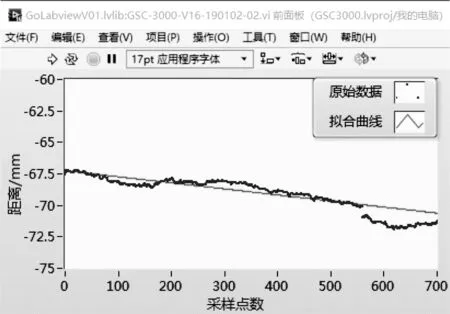
(b)最小绝对残差法图8 线性拟合图

由图8可以看出，最小二乘法拟合的直线与实际测量值存在明显的偏差，尤其在第500个点之后，不能够真实反映原始数据的波动情况，失真情况严重。最小绝对残差法拟合直线与原始数据波动方向一致，比最小二乘法拟合直线更加接近原始数据，可以较好地反映原始数据的波动情况。表3为使用最小二乘法和最小绝对残差法的线性拟合结果。

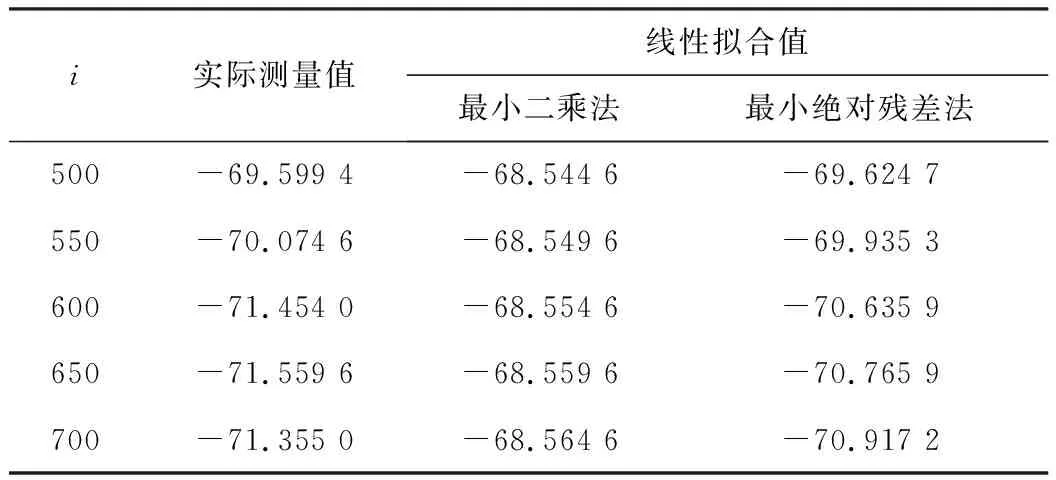
表3 线性拟合结果 mm

表3中，最小二乘法拟合值与实际测量值最大误差达到3mm，显然最小绝对残差法有较高的精度，能够更加真实地还原原始数据的函数关系。

4 现场试验

利用改进后的数据预处理算法分别对5根钢轨进行20次重复试验，分别验证算法改进后扭曲度测量的重复性和稳定性。

4.1 重复性测试

对同一根钢轨，在距轨端1 m的长度对其扭曲度进行重复测量，表4为5根钢轨的扭曲度测试数据。

表4 扭曲度重复性试验结果对比 mm

表4中，极限误差[16-17]是指扭曲度最大值与最小值之间的差值，极限误差反映了测量结果的最大波动范围。系统的极限误差不超过0.066 mm，标准差不超过0.015 7 mm，说明该数据具有较好的稳定性，反映了本系统重复性较高。

4.2 准确性测试

除了验证本系统的重复性之外，还需要考察其准确性。为此，本文随机选取5根钢轨，分别进行人工测量和系统测量，每根钢轨在距轨端1 m处分别测量20次，将人工测量值与系统测量值进行比对。人工测量主要使用电子扭曲尺(精度为0.01 mm)测量。表5为扭曲度试验结果对比。

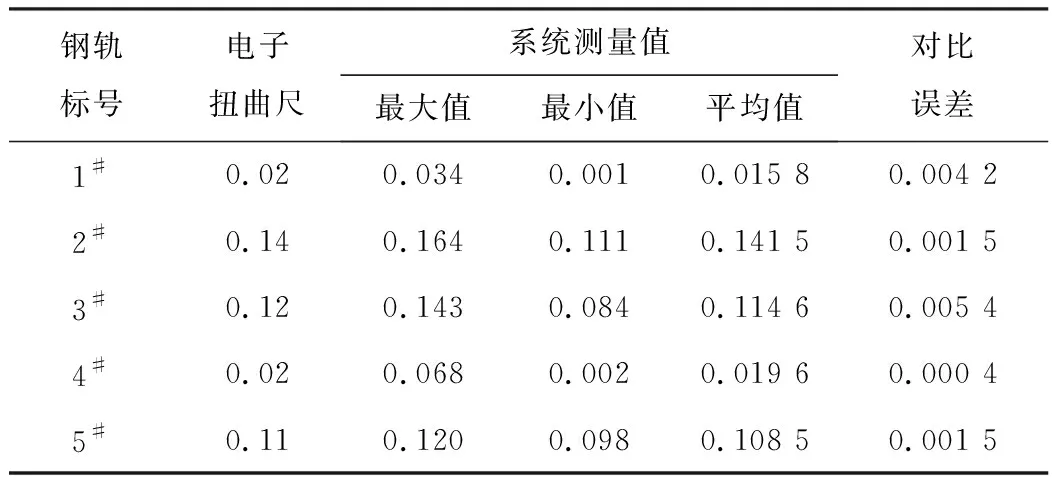
表5 扭曲度稳定性试验结果对比 mm

由表5可以看出，系统测量值与电子扭曲尺测量值的对比误差在0.000 4～0.005 4 mm之间，文献[3]对比误差达到0.01 mm，本系统的精度有了一定的提高。这5根钢轨的电子扭曲尺测量值和系统测量值均满足铁道部规定的合格钢轨的扭曲度不应超过0.45 mm的要求。国内对钢轨检测研究较少，数据也不多，因此本系统应用性较好。

把1号至5号钢轨重复测量20次的数据以图形的形式展现出来，如图9所示。

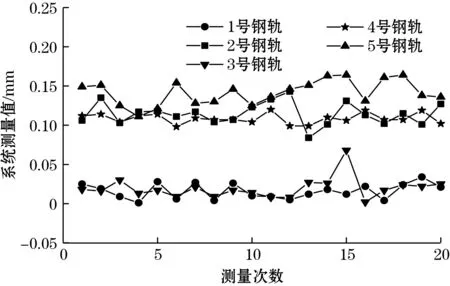
图9 扭曲度试验数据图

从图9可以看出，5根钢轨测量值均没有出现明显波动，可以更加直观地看出系统的稳定性，系统所测的数据皆在0.45 mm以内，与人工测量一致，满足检测要求，系统测量具有较好的准确性。

5 结论

本文主要介绍了基于激光轮廓仪的非接触式钢轨扭曲度检测系统，根据扭曲尺测量方式搭建扭曲度求解模型；利用激光轮廓仪对钢轨廓形进行扫描，通过双正交小波法对激光轮廓仪采集的数据进行去噪处理，RMSE达到了0.319，降噪效果较好；对比改进的最小二乘法和最小绝对残差法对数据的线性拟合，发现改进的最小绝对残差法拟合直线更加接近原始数据波动趋势；最后基于改进的算法进行了大量的实验数据对比分析，验证了系统的重复精度和准确精度。本系统改善了当前人工测量自动化程度低的现状，推动了全自动非接触式钢轨检测的发展。本系统可以应用于长钢轨的焊接中。