基于支持向量回归的飞灰含碳量测量方法
王子铭
(郑州铁路职业技术学院 电气工程学院,河南 郑州 450000)
飞灰含碳量是锅炉运行效率的重要影响因素,对其进行准确、有效的测量有利于调节锅炉燃烧工况,改善热效率,提高电厂的经济效益[1]。但飞灰含碳量受煤质、锅炉运行参数等复杂因素的影响,各因素之间又具有较强的实时性、耦合性及非线性等特点[2],故传统的测量方法准确性较差。目前,我国火电厂常采用人工采样和人工化验等方法对飞灰含碳量进行测量,测量效率较低。因此,需要找到一种飞灰含碳量的计算方法来代替人工测量。
在现有研究中,朱竞东[3]通过分析飞灰含碳量的影响因素,利用BP神经网络建立了飞灰含碳量预测模型,并证明了模型的有效性。Zhao等[4]建立了11-23-1型BP神经网络模型对飞灰含碳量进行预测,预测精度小于6%。李力等[5]利用PSO优化BP神经网络模型,对飞灰含碳量进行了更精确的预测。李智等[6]基于Levenberg-Marquardt的BP神经网络建立了飞灰含碳量预测模型,并通过正交实验分析法得到了锅炉参数。陈敏生等[7]利用人工神经网络建模,采用混合遗传算法进行工况寻优,获得了最佳的锅炉燃烧调整方式。Han等[8]将SVM方法引入燃煤电站锅炉飞灰含碳量预测领域。王春林[9]在采用SVM法对大型锅炉建立飞灰含碳量预测模型后,又讨论了SVM算法中的参数选择问题。Shi等[10]建立了LS-SVM模型对飞灰含碳量进行在线预测。刘长良等[11]、Zhang等[12]利用最小二乘支持向量机的参数优化方法建立了飞灰含碳量预测模型,更适合小样本训练。本研究针对飞灰含碳量的实时性确定其影响因素,建立基于PSO的SVR结构模型,进一步精确地反映了飞灰含碳量。
1 PSO-SVR模型
1.1 支持向量回归
根据给定训练样本{(x1,y1),…,(xl,yl)}⊂(x×y),其中xi∈X=Rn,yi∈Y=Rn,i=1,…,l,寻找Rn上的一个决策函数:
y=f(x)=ωTx+b,
(1)
式中:ω、b是待确定的模型参数,可以用f(x)与y尽可能接近。
为了求解ω和b,将上述问题转化成一个优化问题:
(2)
约束为
(3)
通常并不直接求解式(2),而是引入它的对偶问题:
(4)
约束为
(5)
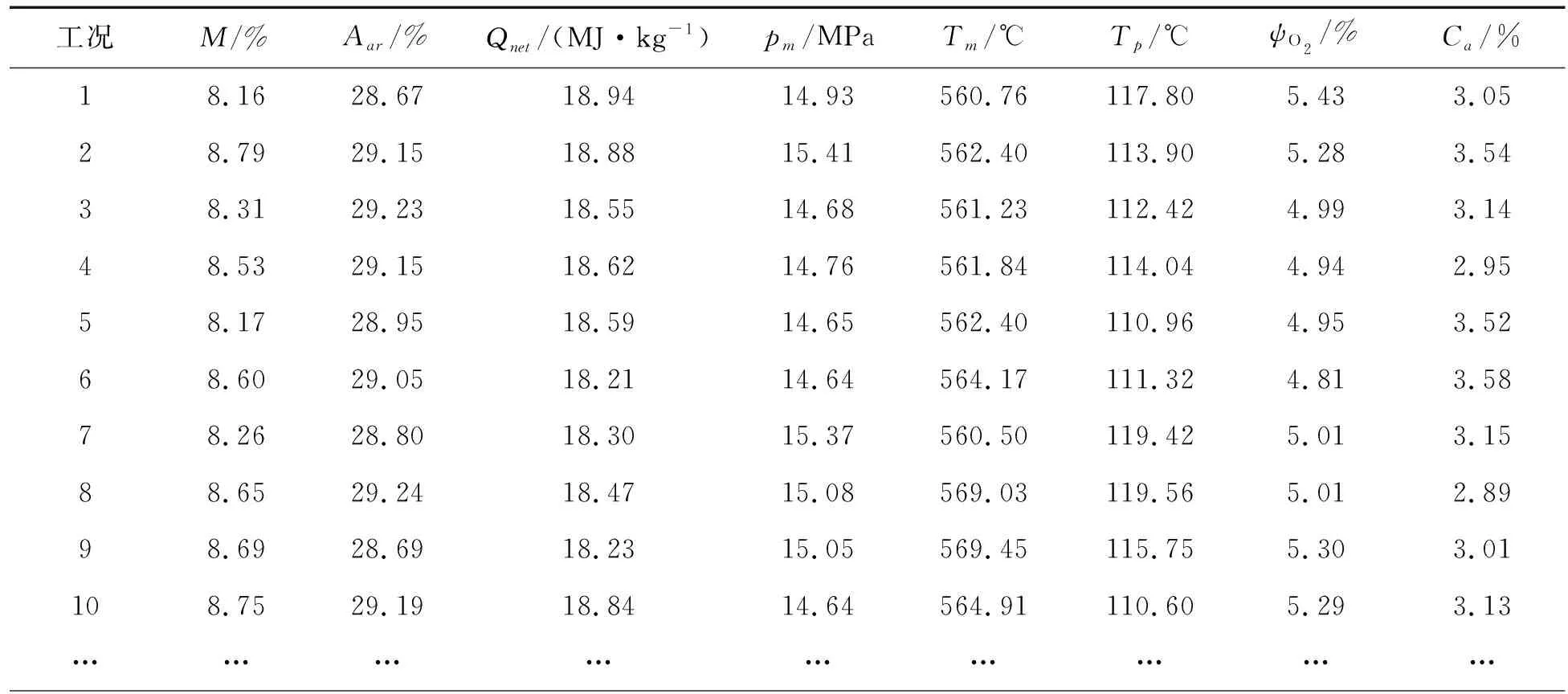
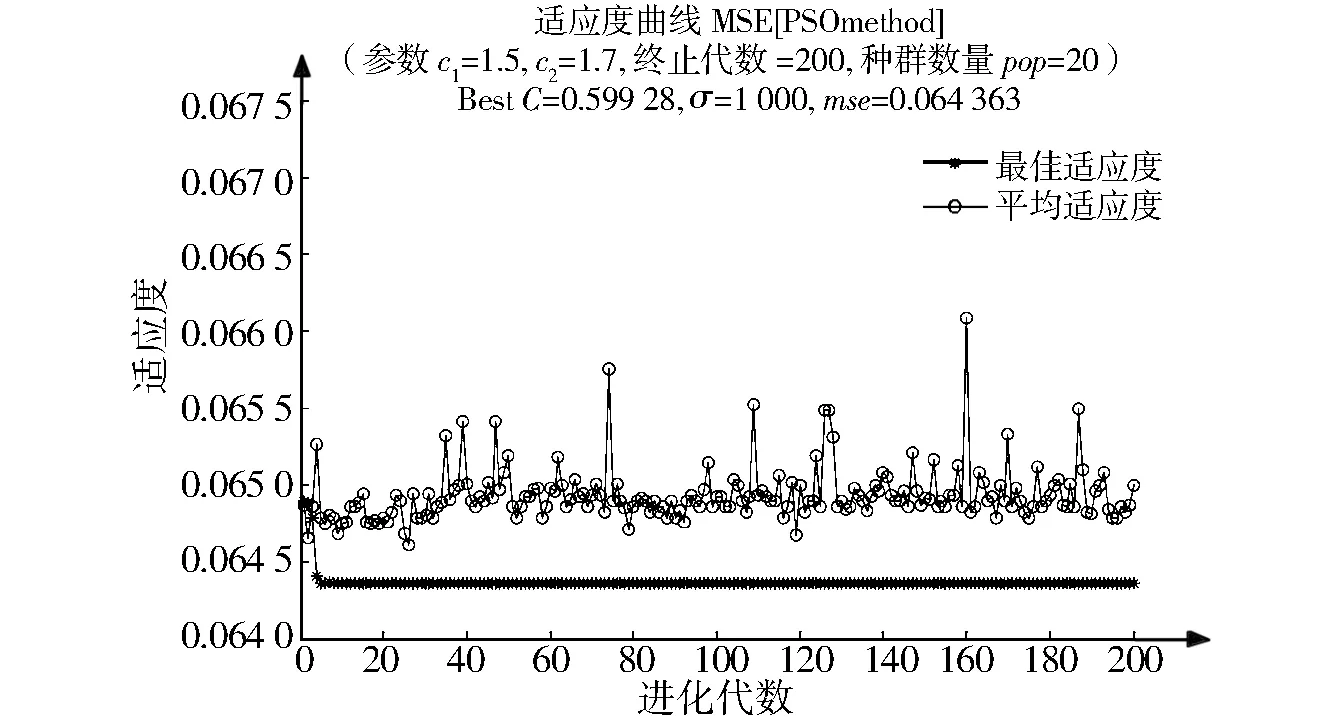
在得到αi后,若0<αi (6) 最终,f(x)可表示为 (7) 式中:k(xi,xj)为核函数。本研究选用RBF作为核函数,见式(8): (8) 粒子群算法是一种群体智能优化方法,其原理可描述为m个粒子在D维空间中搜索目标函数的最优解。每个粒子有3个属性:当前位置xi=(xi1,xi2,…,xiD)、历史最优位置pi=(pi1,pi2,…,piD)、速度vi=(vi1,vi2,…,viD)。在算法迭代过程中,记录粒子的个体最优位置和全局最优位置,其中全局最优位置记为pg=(pg1,pg2,…,pgD)。粒子的速度、位置更新见式(9)和式(10): vid(k+1)=w·vid(k)+c1·rand1()(pid(k)-xid(k))+c2·rand2()(pgd(k)-xid(k)), (9) xid(k+1)=xid(k)+vid(k), (10) 式中:vid(k)是粒子i在第k次迭代中第d维的速度;pid(k)与pgd(k)分别是粒子i在第k次迭代中第d维的个体与全局最优位置;w为惯性权重;学习因子c1和c2是两个非负常数;rand1()和rand2()是在[0,1]生成的随机数;粒子的速度要被限制在[-Vmax,Vmax]。当迭代次数达到设定的最大值或者预定的适应度时,算法停止。 SVR模型的精度在很大程度上由惩罚参数C和核函数参数σ来决定。因此,选择合适的惩罚参数和核函数参数显得尤为重要。本研究利用PSO寻优功能使上述两个参数取得最优值。设不敏感损失系数ε为0.1、粒子位置维数为2,适应度函数采用均方根误差,见式(11): (11) 从现场采集数据中选定训练集和测试集,做坏值剔除和归一化处理,初始化粒子种群,由公式(7)和公式(11)计算粒子的适应度,根据计算结果更新个体极值、全局极值及位置,依次循环,直至找到最优模型,最后通过最优模型对测试集数据进行预测并分析其结果,过程如图1所示。 图1 基于PSO的SVRFig.1 PSO-based SVR 对于特定的锅炉而言,飞灰含碳量(Ca)主要受锅炉负荷和燃烧条件的影响。有研究表明,锅炉中飞灰含碳量受煤炭质量的影响很大,与锅炉负荷成反比,与锅炉燃烧过程中过量空气系数成正比[13]。因此,本研究选取燃料特性、锅炉负荷特性和过量空气系数3个参数作为模型的输入,选取飞灰含碳量作为模型的输出。其中:燃料特性包括低位发热值(Qnet)、灰分(Aar)和煤粉细度(M);锅炉负荷特性包括锅炉主蒸汽压力(pm)、锅炉主蒸汽温度(Tm)和排烟温度(Tp);过量空气系数用含氧量(ψO2)表示。上述燃料特性参数可通过煤炭的工业分析报告获取,每做一次工业分析就更新一次数据;锅炉负荷特性参数可以从电厂DCS系统中获取,该参数具有实时性强的特点,故需要每天多次采集数值,取其均方差作为输入数据。 由上述分析可知,模型的输入参数为燃料特性参数、锅炉负荷特性参数及过量空气系数,输出参数为飞灰含碳量。数据来源于某地区的600 MW燃煤发电机组,模型输入参数来源如前文所述,模型输出参数的原始值来源于人工取样及对实验室化验结果进行降噪处理后获得的65组工况数据。选取这65组数据的前45组作为训练集,用于模型的训练;选取后20组作为测试集,用于验证模型的准确性。原始样本数据如表1所示。 表1 原始样本数据Tab.1 Raw sample data 表1(续) 采用式(12)对样本数据做归一化处理: (12) 在MATLAB软件中使用函数mapminmax实现上述归一化。 采用上述基于PSO的参数寻优方法,设最大进化代数为200、种群数量为20、惩罚参数为[0.1,100]、核参数为[0.01,1 000]、c1初始值为1.5、c2初始值为1.7,运行寻优程序,其适应度曲线如图2所示。在迭代终止时,参数C=0.599 28,σ=1 000,平均适应度在0.065 5以下,最佳适应度基本稳定在0.065以下,模型表现效果较好。 为了验证PSO-SVR模型的准确性,用测试集数据对该模型进行测试,经过MATLAB软件的仿真,PSO-SVR模型测试结果如图3所示。 图2 PSO参数选择结果Fig.2 The result of PSO parameter selection 图3 测试结果Fig.3 The test results 由图3可见,模型拟合度较高。将PSO-SVR模型对飞灰含碳量的预测结果与原始值进行对比,其平均相对误差为0.032 907 55,如表2所示。因此,PSO-SVR模型的精度更高、性能较为优越。 表2 预测结果比较Tab.2 Comparison of prediction results 本研究以燃料特性(低位发热值、灰分、煤粉细度)、锅炉负荷特性(锅炉主蒸汽压力、锅炉主蒸汽温度、排烟温度)、过量空气系数作为影响飞灰含碳量的主要因素,引入粒子群算法解决了SVR模型的精度问题,建立了基于PSO的SVR预测模型,通过测试集的验证,表明该模型精度高、性能优越。1.2 粒子群算法
1.3 基于PSO的SVR参数寻优
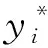
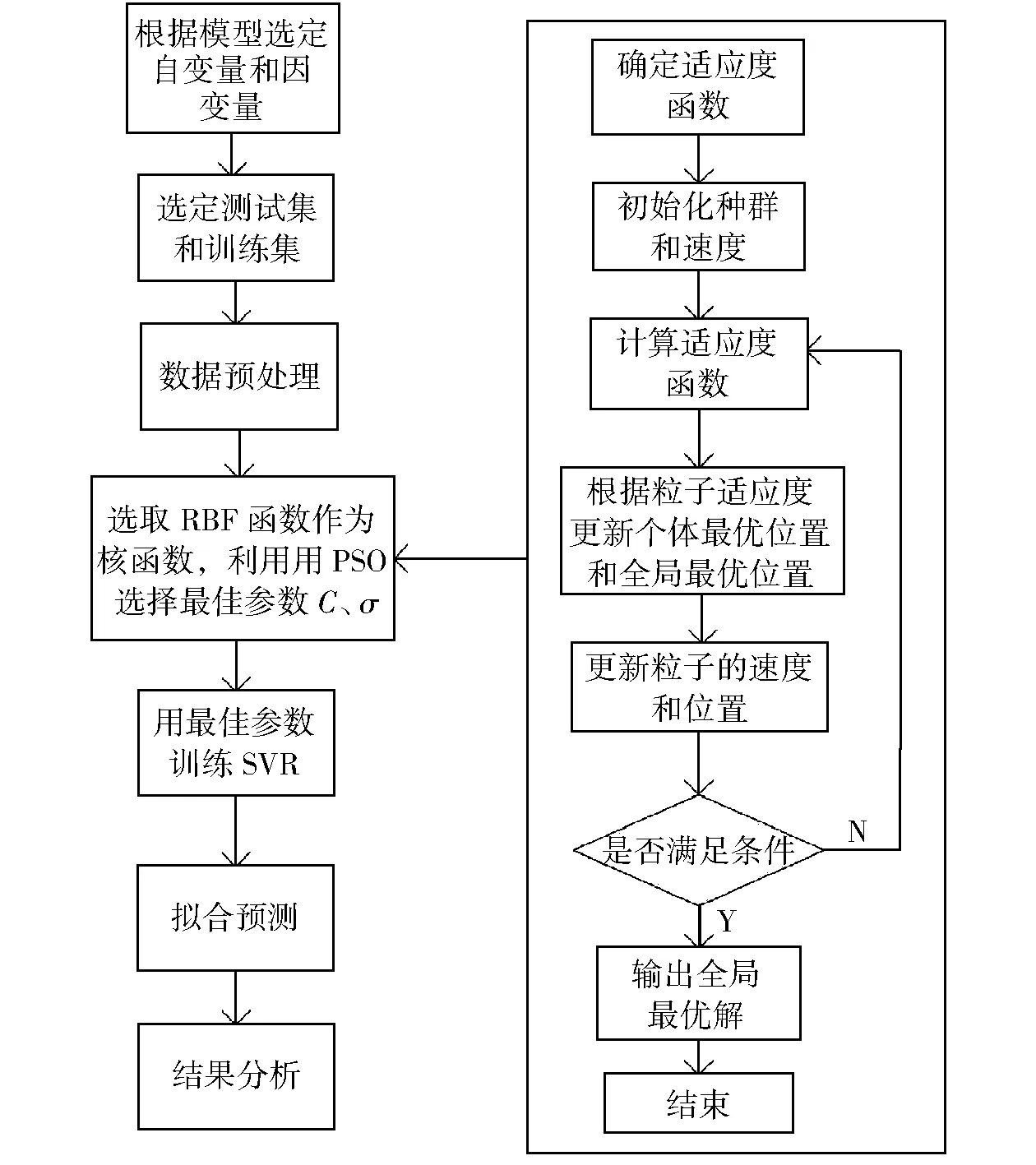
2 基于SVR的飞灰含碳量预测
2.1 飞灰含碳量的影响因素
2.2 数据的选取和预处理

2.3 确定最优参数
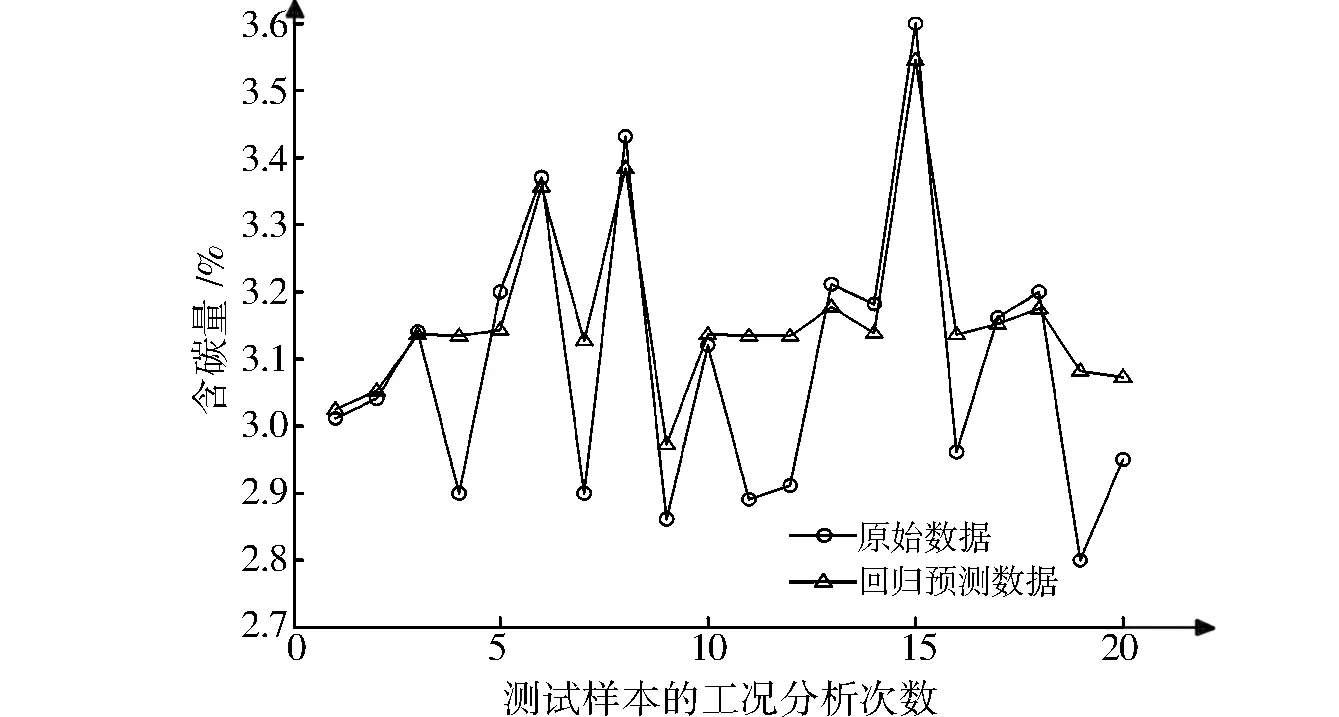
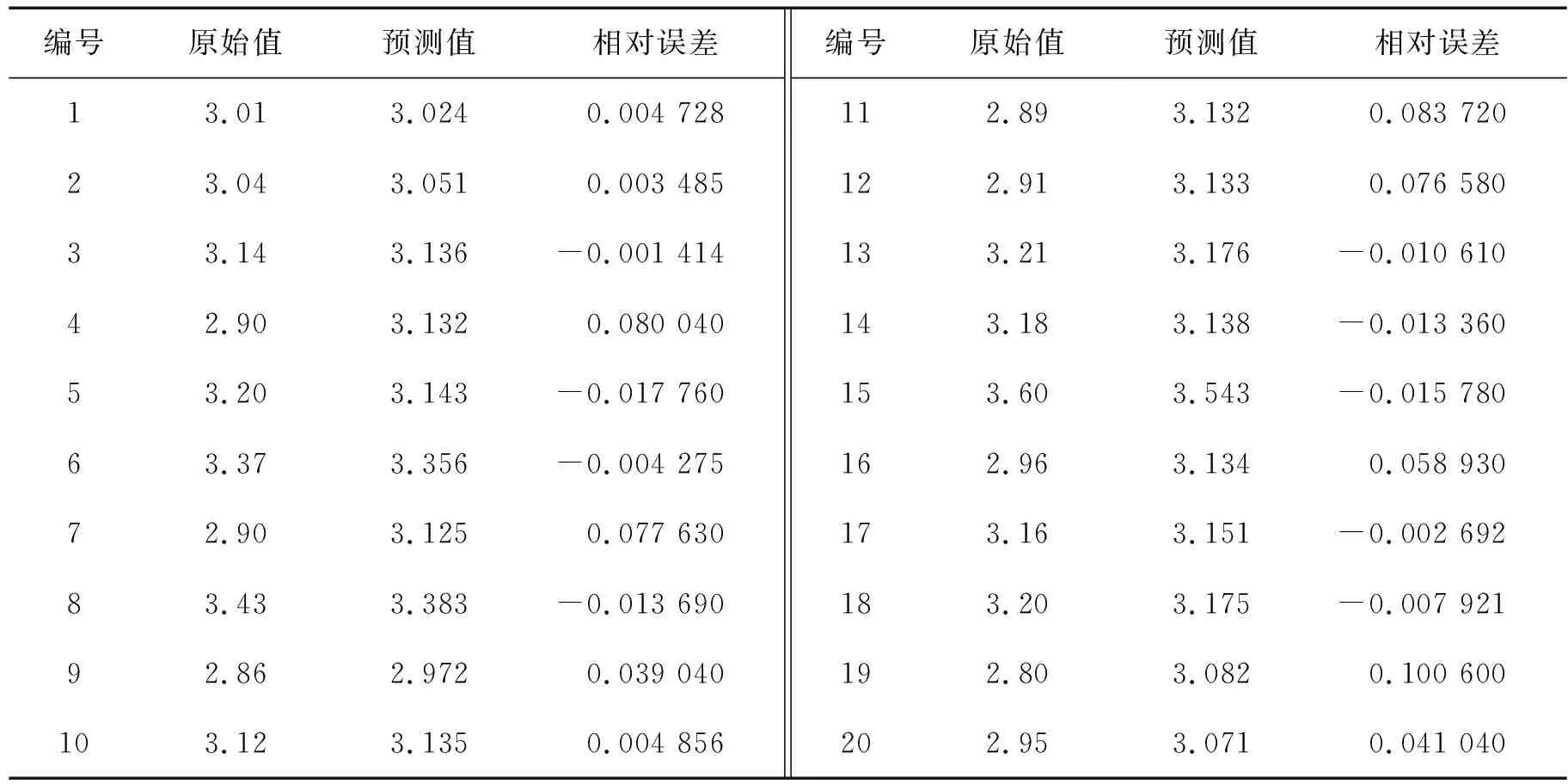
2.4 模型验证与结果分析
3 结语

