基于BP 神经网络陶瓷素坯铣削加工边缘破损预测模型的研究

徐 晗，王维哲，韩 文

(景德镇陶瓷大学 机械与电子工程学院，江西 景德镇 333403)

0 引 言

数控陶瓷坯体雕刻铣削相较于传统的手工雕刻，具有一致性好、效率高、产量大、能雕刻更复杂的图案等优点。但雕刻过程中发生的边缘破损问题将导致陶瓷作品的艺术质量和产品性能的下降，因此，如何有效地减少陶瓷坯体铣削过程中的边缘破损问题，成为提高数控雕刻陶瓷产品质量的关键因素。

陶瓷素烧坯体是通过坯料颗粒之间在没有形成结晶体的情况下相互摩擦和粘连结合在一起。坯料内部存在很多气孔和裂纹。陶瓷素坯在铣削加工过程中，铣削力使加工处颗粒之间相对滑动沿裂纹和气孔等应力场的最小梯度方向扩展[1-3]。当顶面附近的裂纹垂直于加工方向扩展到坯料表面时会形成边缘破损。

国外学者主要对边缘破损产生机理和演化过程进行了研究。基于压痕断裂力学，进行了静载荷作用下的压痕实验及划痕实验，探讨了陶瓷材料产生边缘破损与载荷、裂纹大小、压痕位置和材料断裂韧性等因素间关系，建立边缘破损的数学模型。国内学者则侧重于实验研究，通过具体加工实验研究工艺参数及加工方式对边缘破损的影响。各种研究表明裂纹尺寸，加载应力和断裂韧性是影响边缘破损程度的三个关键因素[4-8]。这些研究主要是涉及工程陶瓷，对于陶瓷素坯铣削加工边缘破损现象研究鲜有报道。

BP 神经网络是一种按误差反向传播算法训练的多层前馈神经网络，具有很强的非线性处理能力，有助于建立非线性模型解决应用问题[9-13]。通过边缘破损尺寸与铣削加工参数映射，可构建一种基于BP 神经网络的陶瓷坯体加工边缘破损预测模型。本文设计了铣削速度、进给速度、刀具锥角、铣削深度和铣削宽度五个因素的正交实验。采用线性回归分析法研究各参数对边缘破损的影响。依据实验数据训练并测试了BP 神经网络预测模型。

1 坯体边缘破损的几何模型

对陶瓷坯体进行加工过程中,数控雕刻机的主轴转速、铣削方式、铣削深度、铣削宽度、进给量等铣削参数对边缘破损产生有影响，而且这些因素的之间影响有相互作用。边缘破损的形状、位置和大小等与铣削参数共同作用有关，导致边缘破损的出现有一定的随机性。在陶瓷加工试验研究中，发现在其加工边缘上经常出现许多大大小小的凹坑。此次实验中加工边缘上产生的这种凹坑的几何形状基本相同，均近似成半圆形，本文将这种几何形状的边缘破损称之为单坑边缘破损[14]。根据对边缘破损形貌特征分析，可建立图1的单坑边缘破损的几何模型。

(1) 工件顶面的破损宽度h：是工件顶面的破损凹坑到铣削侧面垂直距离。其大小与铣削面垂直裂纹的深度和扩展方式有关。

(2) 工件侧面的破损宽度w：是铣削侧面破损凹坑轮廓到工件顶面的垂直距离。其大小与铣削面垂直裂纹的深度和扩展方式有关

(3) 工件侧面的破损长度l：是破损凹坑缺口的长度。其与铣削材料表面平行裂纹及其扩展有关。

从加工陶瓷坯料破损现象分析，侧面破损宽度w 与破损长度l 与顶面破损宽度h 成正比增大，此处只需要分析顶面破损宽度h 一个变量即可反应边缘破损的情况。

2 基于BP 神经网络的边缘破损预测模型

BP 神经网络是一种多层前馈神经网络,具有信号前向传递,误差反向传播等特点[15,16]。

BP 神经网络模型主包括输入层、隐层和输出层。输入层神经元数依据试验的铣加工参数确定，为5 个神经元，分别代表铣削速度、进给速度、刀具锥度、铣削深度及铣削宽度。输出层神经元数依据试验的目标确定，为1 个神经元代表预测的顶面破损宽度h。在三层网络中，隐含层神经网络神经元数N2和输入层神经元数个数N1之间的近似关系如式(1)所示：

故隐含层神经元数为11 个。其模型结构如图2 所示。

基于BP 神经网络陶瓷坯体铣削加工边缘破损模型的训练流程为：

(1) 批量输入学习样本并对输入量和目标量进行归一化处理；

(2) 参数初始化，设置最大训练次数、学习精度、学习速率、对权值及阈值赋值；

(3) 前向传播，分别计算隐含层、输出层各神经元的输出；

(4) 计算对目标样本量产生的误差；

(5) 达到要求精度或者训练次数，如果是，则预测模型建立；否则，进行第六步；

(6) 反向传播，计算输出层上各神经元的梯度值，并调整该层上连接的权值及阈值；

(7) 反向传播，计算隐含层上各神经元的梯度值，并调整该层上连接的权值及阈值；

(8) 输入下一样本，依次循环。

基于BP 神经网络陶瓷坯体铣削加工边缘破损模型的测试流程为：

(1) 输入测试样本并进行归一化处理；

(2) 输入到神经网络预测模型中；

(3) 预测值反归一化；

(4) 计算预测值与实验值的误差。

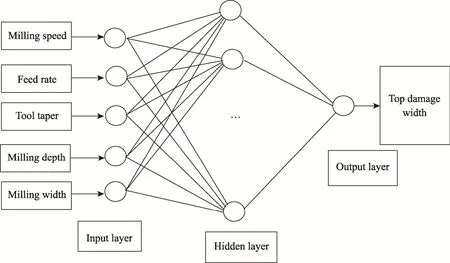
图2 基于BP 神经网络的预测模型结构图Fig.2 Structure chart of the prediction model based on BP neural network

3 实 验

3.1 实验设计

为了研究日用陶瓷坯料铣削加工所产生的边缘破损与铣削加工参数之间的变化规律，设计了600 °C 素烧陶瓷坯料的铣削加工的正交实验表。实验设备、检测设备及铣加工原理示意图见图3。

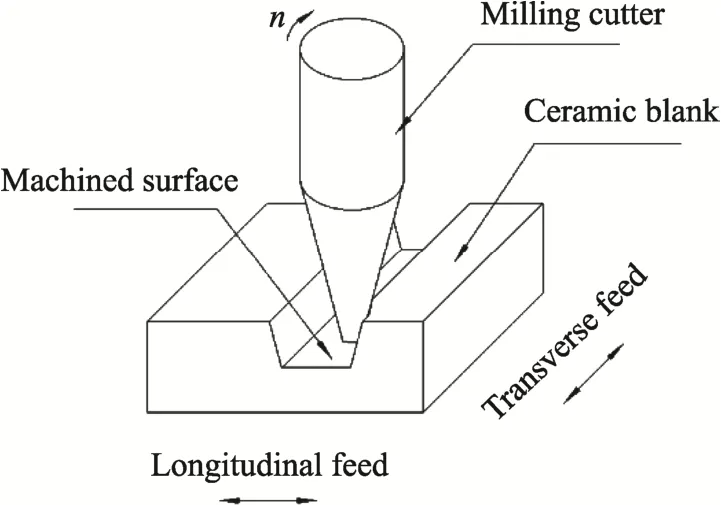
图3 实验设备、检测设备及铣加工原理示意图Fig.3 Schematic diagram of the experimental set-up, testing equipment and milling principle

(1) 实验所用的设备为自制龙门立式三轴数控雕刻机。设备控制软件采用改进的Mach3 软件，用于600 °C 素烧陶瓷坯料的铣削加工。

(2) 实验所用的陶瓷坯体为经过600 °C 素烧的陶瓷坯体。该坯体发生部分氧化分解反应，坯体中的结构水分解排除，坯体失重明显，气孔率加大。部分颗粒间发生化学反应，强度有一定的增加。

(3) 实验所用的铣刀为威特3.175 雕刻刀钨钢平底尖刀。刀尖为直径1 mm、刀具锥度有15 度、20 度、25 度和30 度四种。

3.2 加工方式及铣削参数

采用立铣、侧铣；铣削方式为顺铣；不加切削液，冷却方式为空气自然冷却；走刀路线为直线。分析铣削用量(铣削速度、进给速度、刀具锥度、铣削深度和铣削宽度)对边缘破损的影响规律。采用五因素四水平进行正交试验，铣削参数如表1所示，选用L16(45)正交试验表。

表1 铣削参数因素水平表Tab.1 Level and factor of the milling parameter

3.3 边缘破损预测模型

在铣削试验完成后，在加工范围内取5 个边缘破损严重位置，通过USB 数码显微镜的CCD图像采集系统对已加工表面进行显微放大并拍摄照片。利用 USB 数码显微镜配套的测量软件Measurement，测量其上表面的边缘破损凹坑到正棱的最大垂直距离h，求取平均值。表2 和表3 的试验结果分为训练样本和测试样本。4 个测试样本按铣削速度的四个试验水平分别抽取3、7、10、14 号实验组成。

首先，对表2 的训练样本和表3 的测试样本进行归一化处理，最大训练次数选为1000，神经网络预测模型基本参数见表4。经12 组训练样本训练4 次后，所有训练样本误差达到预先设定的精度1 e-7，神经网络模型建立完成。

训练样本预测值与试验值的变化见图4。

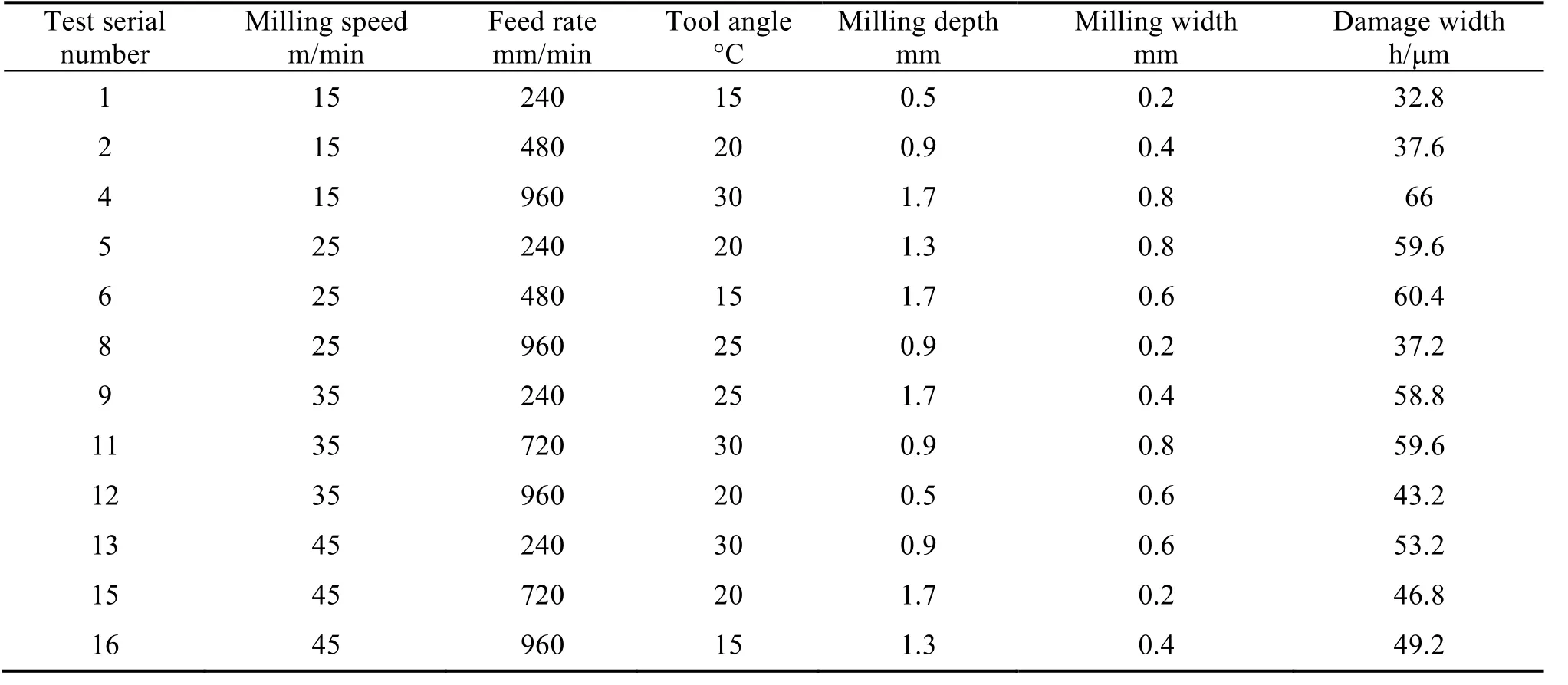
表2 预测模型所需的训练样本参数表Tab.2 Sample parameters required for the prediction model

表3 预测模型所需的测试样本参数表Tab.3 Sample parameters required for the prediction model

表4 神经网络结构参数及函数Tab.4 Structural parameters and functions of the neural network

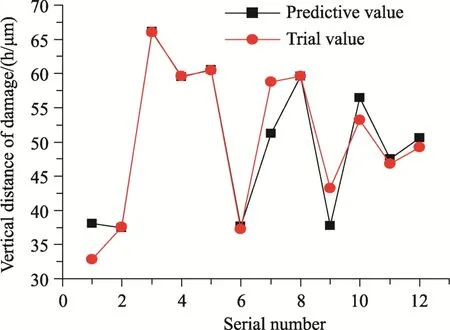
图4 训练样本预测值与试验值的变化图Fig.4 Variations of predicted and tested values of the training samples

4 结果分析

4.1 边缘破损预测模型误差分析

针对所建立的各预测模型，边缘破损的预测误差定义如式(2):

式中，Err 为预测误差值，ha为试验值，hp表示边缘破损神经网络预测值。将表3 的测试样本代入所建立的预测模型中，求出测试样本相应的预测值和预测误差，具体结果见表5。通过对比测试样本的试验值和预测值之间的误差来反映各预测模型的预测效果。

从上述图表中可以发现，边缘破损的预测误差在6.59%-9.65%范围内，证明了BP 神经网络能够反映铣削参数和边缘破损ha之间的非线性关系，有助于在日用陶瓷铣雕刻加工中选择合适的工艺参数。

表5 边缘破损的预测值和预测误差Tab.5 Predicted values and prediction errors of edge breakage

4.2 铣削参数敏感性分析

基于正交实验测试数据，采用线性回归分析方法，建立600 °C 素烧坯料铣削加工过程中的边缘破损顶面破损宽度h 经验模型如式(3)：

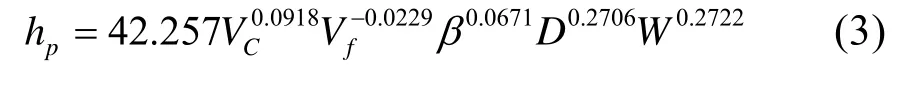
根据经验模型各铣削参数项指数绝对值的大小，可确定边缘破损顶面破损宽度h 对各铣削工艺参数的相对敏感性。对各铣削参数指数绝对值进行归一化处理，得到如图5 所示的铣削参数相对敏感性图谱。

图5 铣削参数对边缘破损的敏感性Fig.5 Sensitivities of the milling parameters to edge breakage

从图5 可看出，铣削宽度和铣削深度对边缘破损h 影响最大，贡献率分别达37.57%和37.34%。进给速度影响最小，贡献率仅为3.16%。铣削速度、刀具锥度两者对其影响相近，贡献率分别为12.67%和9.26%。相对敏感性表明了各铣削参数对边缘破损h 作用的主次顺序。

5 结 论

(1) 为预测素烧坯料铣削加工过程中的边缘破损顶面破损宽度h，考虑了铣削速度、进给速度、刀具锥度、铣削深度及铣削宽度对素烧坯料铣削加工边缘破损的影响，铣削宽度和铣削深度对边缘破损h 影响最大。

(2) 建立基于BP 神经网络边缘破损顶面破损宽度h 预测模型，并通过试验验证模型的预测精度。结果表明: BP 神经网络模型的预测精度均较高，预测误差均在10%以内。该预测模型为陶瓷素烧坯料铣削加工过程中的边缘破损预测提供一定的借鉴。