利用“将军饮马”解决线段最值问题

贺建伟

“将军饮马”模型是解决线段和的最小值，线段差的最大值问题的经典模型，也是陕西中考14题，25题的常考题型。解决此类问题的关键是要理解知识背景及解题思路和策略！

类型一：两定点在直线的异侧时求两线段和的最小值

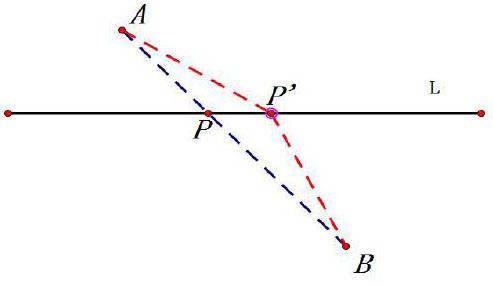
问题1：在定直线L上找一点P，使得P到定点A，B的距离之和最小，即AP+BP的最小值。

结论：当A，P，B三点共线时（即点P为线段AB与直线的交点时），AP+BP有最小值为线段AB的长！

证明：在L上任意取一点P（不与P重合），连接AP BP，在三角形ABP中有AP+BP>AB。所以当A，P，B三点共线时AP+BP有最小值为AB的长！

类型二：两定点在直线的同侧时求两线段和的最小值

问题2：在定直线L上找一点P，使得P到定点A，B的距离之和最小，即AP+BP的最小值。

结论：作A或者B关于直线L的对称点A或B，再连接AB或者AB为AP+BP的最小值！

依据：两点之间线段最短、三角形任意两边之和大于第三边！

类型三：两定点在直线同侧时求两线段差的最大值

问题3：在定直线L上找一点P，使P到A，B的距离之差最大，即AP-BP绝对值的最大值。

结论：当A，B，P三点共线时（即点P为线段BA的延长线与直线的交点时）AP-BP的绝对值有最大值为AB的长。

证明：在L上任意取一点P（不与P重合），连接AP  BP 在三角形ABP中AP-BP的绝对值小于AB。所以AP-BP绝对值的最大值为AB的长！

类型四：两定点在直线异侧时求两线段差的最大值

结论：作A或者B关于直线L的对称点转化为类型三即可得出AP-BP绝对值的最大值！

模型应用：例1：如图：在边长为2的菱形ABCD中，角DAB=60，E是AB邊上的一点，且AE=1，点Q为对角线AC上的动点

解析：（1）求三角形BEQ周长的最小值

例2：如图：在锐角三角形中，AB=4，角BAC=45，角BAC的角平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值。

解析：作B关于AD的对称点B，则BM+MN=BM+MN。所以当B、M、N共线且与AB垂直时BM+MN有最小值为BN的长！