车载动力电池成组热不一致性研究

郭健忠，张华伟，张麒麟，许小伟

（1.武汉科技大学汽车与交通工程学院，湖北 武汉 430065；2.山东同创汽车散热装置股份有限公司，山东 泰安 271411）

1 引言

为满足车载电力驱动系统的性能要求，单体电池通常会采用串并联成组形式来突破自身电压与容量的限制。然而单体电池在制造与使用过程中产生的不一致性，如电池内阻、荷电状态差异，则造成成组后各分支电路上电流分配不均，从而产生温度差异，长时间使用，还会导致电池组加速衰退。因此，评价电池系统的性能指标需要综合考虑各单体电池运行时的热均衡程度，才能确保对电池组整体性能的准确评估。

国内外关于电池成组性能的早期研究大多集中在串并联电池组电学状态量的不一致性分析上，例如分析单体电池在内阻、容量与荷电状态存在差异性时的并联支路电流分配不均衡情况[1]、单体电池不同成组方式对整体一致性与安全性的影响[2-3]。对于电池成组热一致性分析的研究大多集中在温控系统设计与控制策略方法上[4]；未对大规模电池系统内部温度不一致性产生的原因进行深入探讨，且现有电池成组模型与热模型的衔接计算方面不太完善[5-7]。可在已建立的针对磷酸铁锂电池电、热模型的基础上对模型进行简化与耦合，提出可实时估算电池串并联成组内部温度变化的仿真方法，通过模拟电池包真实的动态电流输入，研究影响动力锂离子电池成组内部温度不一致性的多种因素，并形成有效的电池串并联成组后热不一致性分析手段。

2 单体电池模型分析

2.1 电池模型简化处理与耦合计算方法

选用额定电压为3.3V、容量20Ah 的软包磷酸铁锂动力电池作为研究对象，为能够在保证模型精度的条件下，根据研究对象的特点简化电池电、热学模型，以较小的计算量来分析串并联成组后单体电池温度响应特性。

通常为分析电池电学响应中的平衡电势特性与超电势特性，研究人员设计了大量等效电路电学模型[8]，利用数学模型来拟合电池迟滞电压效应；利用等效电阻元件与n 阶RC 网络结构的串并联形式来模拟电池电极偏离平衡电势时的外特性，最后输入电流，并输出电池端电压响应。

电池充放电时的平衡电势曲线特点类似于磁性体的磁滞回线，为了描述电池的迟滞效应，一般可将等效电压源看成平衡电势EMF 与迟滞电压Vh 两部分组成，并且将其看成随电池荷电状态SOC 变化的函数。

文献[9]中将某磷酸铁锂电池的迟滞电压看作成在充放电过程中限制于一定范围内变化的变量，而实际上其迟滞电压的数值在SOC 处于（10～90）%的区间内的上下浮动电压仅为5mV；文献[6]中分析得出磷酸铁锂电池在电压平台段时的迟滞电压相对稳定，而研究中采用的磷酸铁锂电池的电压平台段通常位于SOC 状态在（10～90）%之间，则简化后的充放电两阶段迟滞电压则为：

式中：iRj—某一RC 容阻结构中的极化电阻电流；j—RC 容阻结构阶数；Δt—迭代时间步长；RjCj—时间常数。

模型内部RC 网络结构的阶数越高、拟合电压渐变段的精度就越高，但模型计算量越大，在电池结束放电的过程中，RC 网络结构由零状态响应转变为零输入响应，在电压跳变之后的渐变过程中，电压都，如式（3）所示。将实验得出的电池电压回弹曲线与函数式（4）进行拟合可获得相应的模型参数。

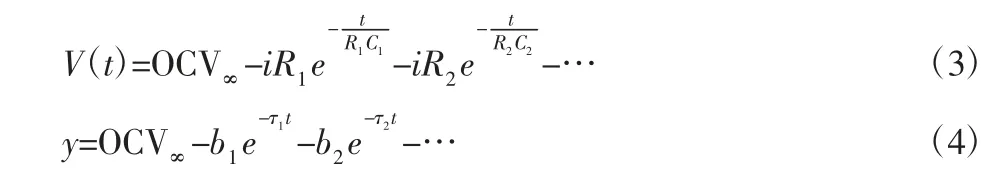
式中：OCV∞—静置时间足够长的理想OCV 电压；Rj=1，2…—各极化电阻；bj=1，2…—拟合的各极化电阻数值；τj=1，2…—拟合的CjRj数值的倒数。

分别使用一阶、二阶与三阶RC 网络结构进行回弹曲线的拟合。电池45℃时采用C/2 放电倍率脉冲放电后静置阶段测量得到的电池回弹OCV 实验数据与不同阶数的RC 网络拟合的回弹电压进行重叠比较，一阶RC 网络拟合误差较大，而二阶与三阶RC网络结构产生的误差变化不明显，因此这里的电学模型可简化使用二阶RC 网络结构，如图1 所示。

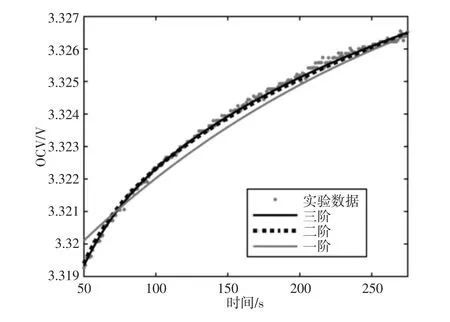
图1 不同阶数RC 网络拟合的回弹电压曲线Fig.1 The Curve Fit Different Order RC Network for Rebound Voltage

SOC 在电流值测量精确、校准采样点量多时，采用安时积分法进行SOC 状态估计的可靠性较高[11]。将电学模型中的SOC、极化电阻支路电流iRj作为状态量，电池端电压V 与迟滞电压作为输出量可得：

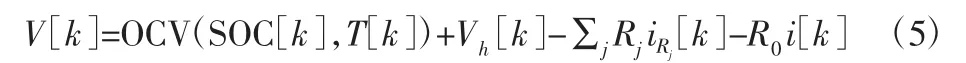
式中：Q—电池容量；R0—欧姆电阻；Rj—某RC 容阻结构中的极化电阻。

文献[5]中提出的等效热模型将电池的产热源简化为可逆反应热与电阻耗散热，如式（6）所示。由于软包电池的厚度间距小，可简化热量从电池芯部向电池表面传热的热阻，即电池核心温度与电池表面温度相等。同时与电学模型进行联合计算，对热模型方程进行时间离散化处理，相关方程如下所示：

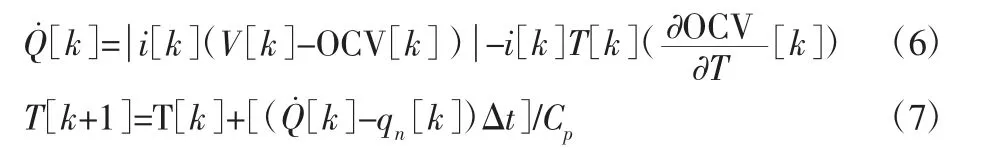
式中：Q˙—单体电池的生热率；q—电池散热率；Cp—电池质量与比热容的乘积。

文献[12]中根据等效比热容计算公式得到的磷酸铁锂电池的比热容为40.6J/（kg·℃·Ah），所使用450g 磷酸铁锂电池的Cp可近似估算为365.4J/℃；电池包为达到IP67 标准采用密封封装隔，无强制散热装置的电池散热功率可忽略不计。

为了计算电池在特定电流输入下的电压与温度响应，需要进行电热耦合计算，方程耦合计算的初始条件需要设置电池的初始SOC、支路极化电阻初始电流iRj，电池初始温度与仿真时间步长Δt。电热耦合模型中与温度T、SOC 状态量相关的OCV 需要在每个时间步长开始前更新，实现双向耦合。

2.2 OCV 关系曲线测量数据分析

单体电池的开路电压OCV 是关于电池荷电状态与温度的静态变量，采用美国Arbin 公司的BT-2000 测试系统进行电池循环充放电测试。

采用C/30 充放电倍率充放电至电池厂商规定下25℃电池最小、最大切断电压来得到整个充放电过程中近似平衡状态的电池SOC-OCV 关系曲线，如图2 所示。由于实验中充放电倍率较小，在整个充放电过程中可忽略电池内部极化电压与内部电阻耗散热对OCV 产生的影响。实验采用相同的步骤分别在（-5）℃、5℃、15℃、25℃、35℃、45℃六种温度下进行充放电测试。

图2 电池45℃时SOC-OCV 拟合关系曲线Fig.2 SOC-OCV Fitting Curve of Cell at 45℃

由于其他温度下的截止电压都设置为25℃时的切断电压，导致进行充放电实验采集的数据会在SOC 状态接近0%或100%时提前到达截止电压，导致缺少部分SOC 状态时的OCV 数据。数据使用加减内阻来估算近似各温度下电池的SOC-OCV 关系曲线，45℃下SOC-OCV 关系曲线，电池荷电状态SOC 在（10～95）%区间内有明显的电压平台段，而在此区间外的OCV 受SOC影响很大，如图2 所示。

为得到电池OCV 与温度T 之间的关系，可采用的线性形式拟合OCV 随T 与SOC 之间的关系[11]，如式（8）所示。其中：B—OCV 随T 的变化率，此法相比于文献[5]中直接测量法更简单。

OCV（SOC，T）=OCV（SOC，0）+T·B（SOC） （8）

由于电池在0℃以下的高电阻值造成拟合关系的精度下降，选用0℃以上的数据进行关系拟合分析。对应的每个特定温度下，利用最小二乘法强制拟合线性关系。

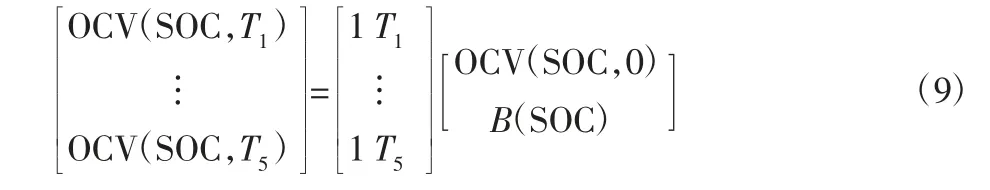
式中：Ti=1～5—5℃、15℃、25℃、35℃、45℃五种测试温度，由于电池生热温度一般高于环境温度25℃，而对于25℃以上拟合关系与实测数据的均方根误差均在3.2mV 以内，说明式（8）线性关系的拟合效果良好。

3 电池成组模型分析

3.1 电池串并联成组模型简化分析

电池组内最小电压、容量离散量都取决于单体电池的性能，而对于电池串并联成组的性能主要是通过电池参数分布差异造成的不一致性、电池成组方式与电池成组后运行工况特点决定的。

电池成组方式一般可分为先并后串或先串后并两种形式，电池等效电压源可简化为不受支路电流影响的OCV 与受电流影响的施加在电池欧姆内阻上的电压降两部分。

在先并后串（PCM）成组方式中，定义在k 时刻j 支路上通过的电流为ik，j，电阻为R0，j，Np为并联支路数，ik为k 时刻电池包总电流。根据基尔霍夫电压定律，PCM 中各并联支路上的端电压vp均相等，由基尔霍夫电流定律可知，各并联支路上的分支电流总和为电池包的总电流，则PCM 中各并联支路上的电流就可算出：

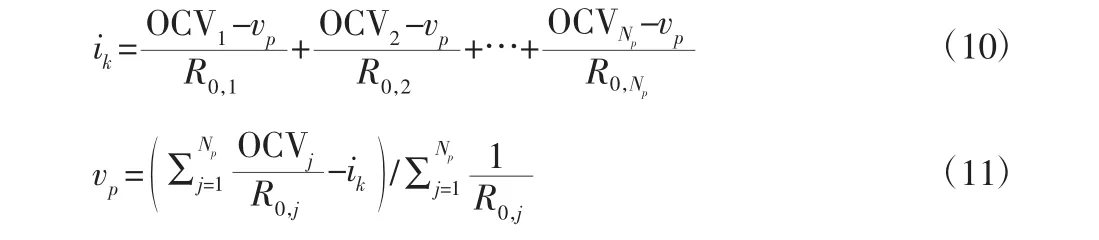
对于先串后并（SCM）成组方式，各并联分支电路上由Ns个单体电池串联而成，且各并联分支上流经的电流相同，则其等效电压源可集总表示为总体OCV 与总体欧姆内阻造成的电压降，并按照PCM 结构来计算各分支电流的分布情况。

3.2 电池组动态电流需求分析

为模拟车载动力电池组真实的动态运行情况，需构建针对某动力传递路径的数学模型，并利用标准测试循环工况作为输入，输出车载电池包在实际运行过程中的动态电流需求。

由于电动车续航里程与车载电力驱动系统电压输入的性能要求限制，如车载电池包需要输出320V、60Ah 的性能指标，根据研究对象的基本性能，则需要单体电池3 节并联与96 节串联的成组形式，通常可分成48 个串联的3 节并联与2 节串联的成组模块，方便BMS 系统进行管理。整车仿真中速度变化是根据1Hz更新频率的行驶循环工况输入给定的，车辆需在速度更新时间内进行恒定加速过程，将初始速度Vprior加速到期望速度Vdesired，同时可算出车辆的期望加速度adesired。车辆在行驶过程中所期望的力矩Tdesired传递至车轮用来克服车辆的行驶阻力，其中包括了加速阻力Fa、空气阻力Fd、滚动阻力Fr和坡道阻力Fg。

由于受到车载电机扭矩外特性限制，在电机处于恒定转矩工作区域时，可提供最大力矩为电机额定最大力矩Trated-max；而在恒定功率工作区域内，可提供最大力矩则根据电机转矩外特性曲线计算得到。车辆减速时存在能量回收过程，需考虑整体电力传输的再生效率。由车辆实际所得扭矩Tactual与加速度aactual计算在电机最大转速限制下的实际车速Vactual[13]，并作为初始速度进行下一时间步的循环过程。

假设电池包在每个更新频率内都有足够的电量可提供则电机所需电池包提供的功率Pm为：

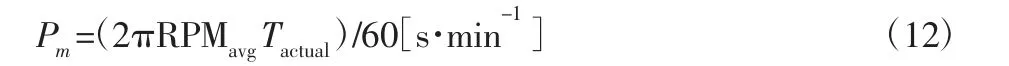
式中：RPMavg—时间步长内的平均转速，取初始转速与真实转速的平均值。

由于电动车在能量回收过程中可能造成电池过充现象，为了避免发生，电池荷电状态应保持在（10～90）%之间为宜，而此时正处于电池的电压平台段，可假设在车辆运行过程中电池输出的为恒定的额定电压vnom，则电池的需求电流输出为：

式中：Ptotal—考虑其他车载设备用电需求的总需求功率。

在实际运行中的电机对电池组的需求电流是动态变化的，电池包在整个工作过程中不断进行充放电循环，如图3 所示。而总电流还需分配到各支路上，此时则需要考虑电池的成组方式与电池的参数差异分布情况。

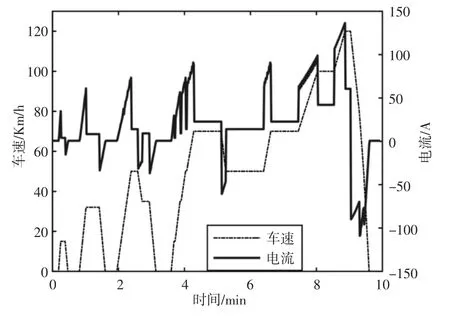
图3 ECE+EUDC 循环工况运行仿真图Fig.3 Simulation for Running at ECE+EUDC Cycles

4 仿真与结果分析

电池成组热不一致性主要体现在各单体电池间的温度差异上。分析电池成组模型与单体电池模型中参数，电池温度变化特性主要取决电池的输入电流、电池内阻与荷电状态，而各分支上电池的输入电流取决于电池成组方式，电池包内3 节并联与2 节串联的结构可分为先并后串与先串后并的两种成组方式进行研究。

4.1 电池内阻差异的影响分析

为了有效分析电池内阻对成组模块热均衡性能的影响，文献[3]中选取差异程度偏大的电池进行了循环充放电实验，其最大内阻偏差为28.2%；本次研究选取的工况为图3 所表示的短期内车辆运行时的循环工况，可简化处理不考虑电池内阻随循环工况而增大的衰退现象。仿真假设某单体电池内阻存在较大差异，设置内阻偏差值分别为10%、20%、25%，各电池初始SOC 设置为90%，将电池包的动态需求电流分别输入至2S3P 和3P2S 成组模型中。电池在连续循环工况输入下，电池内阻差异性造成的电池成组模块内最大温差变化的情况，如图4 所示。

图4 不同内阻差异下电池组最大温差Fig.4 The Maximum Temperature Difference Caused by Internal Resistance Inconsistency

可知两种成组方式的最大温差均随循环工况次数、电池内阻偏差增大而上升。3P2S 成组方式下的最大温差在前期略偏大，但在输入13 次循环工况后最大温差的增长趋势呈递减状态，最大温差趋于稳定状态；而2S3P 在10 次循环工况后则超过3P2S 的最大温差并继续加速上升。其中内阻差异为20%、25%的2S3P 成组方式下，连续23 次循环工况运行超过4℃，在锂离子电池组适宜温差范围上限之外；相比之下，3P2S 最大温差则接近3℃，且趋于平稳状态发展。

4.2 电池SOC 差异的影响分析

电池闲置过程中自放电率差异性会导致电池组内部SOC 状态量的不一致性，而较大的SOC 差异则造成各并联支路在工作状态时系统均衡度失稳。在不考虑内阻差异的情况下设置某单体电池SOC 状态存在差异性，其偏差设置为10%、20%、30%，并在之前的基础上分析电池SOC 差异对成组模块内部热均衡性能的影响。电池成组模块内由SOC 差异性导致的最大温差变化情况，两种成组方式的最大温差都随着循环次数与SOC 差异程度的增加而上升，如图5 所示。

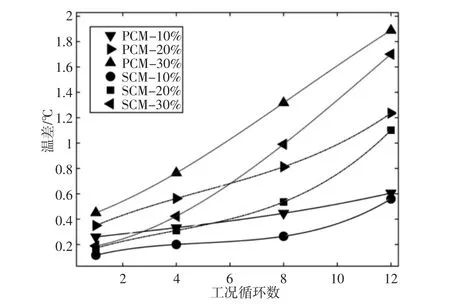
图5 不同SOC 差异下的最大温差Fig.5 The Maximum Temperature Difference Caused by SOC Inconsistency

总体上2S3P 连接方式的最大温差要小于3P2S，在输入12次循环工况后的最大温差均小于2℃，但整体变化增长率趋势不断增大。电池SOC 已脱离电压平台段，而有些电池仍处于电压平台端，导致后期最大温差急剧上升。整体上两种成组方式对SOC 存在差异性的影响并不大。

5 结论

研究中提出的电池串并联成组仿真方法可以较小的计算量对成组模块内部存在内阻或荷电状态差异性时的热不一致性情况进行分析研究。根据软包磷酸铁锂电池研究对象的特性，二阶RC 网络结构与电压平台段简化迟滞效应模型具有较好的拟合效果；利用线性拟合关系拟合得到的近似OCV 误差小，可作为相关电池模型参数的简化测量手段；描述动力传递路径的数学模型可以表现出电池包在实际运行过程中电流的动态情况；对于电池梯级成组利用时电池内阻存在较大差异性时，应尽量采用先并后串的成组方式；电池存在的SOC 差异性在循环运行过程中会不断增大，应尽量保持在电压平台段对应的SOC 区域内运行。