基于灰色系统理论的基坑钢筋应力监测分析

邸健，张旭晴，杨国东，张元元

1.吉林大学 地球探测与科学技术学院，长春 130026;2.北京市勘察设计研究院有限公司，北京 100038

0 引言

近年来，中国基坑工程呈现出新的难点，主要表现为基坑工程所处环境复杂、周围管线众多且建筑物密集、环境保护要求高。因此，基坑支护结构除满足自身的强度要求外，还需要满足变形要求，确保基坑周围的建筑物和管线可以正常使用，基坑工程的设计和施工逐渐从强度控制转向变形控制。基坑支护结构变形分析与预报也逐渐成为众多学者的主要研究方向。

邓聚龙于20世纪80年代提出灰色系统理论学说，主要解决一些包含未知因素的特殊领域问题，且随着应用领域的逐步扩大，灰色系统理论被引入到岩土工程中，使得中国施工人员可以更加方便地实施基坑建设[1-3]。灰色系统理论具有使抽象系统实体化、模型化、量化和优化的功能，其中GM(1，1)模型是灰色系统理论中最重要的模型，目前针对该模型的研究越来越多，姜刚等[4]基于GM(1，1)灰色模型、小波分析和神经网络结合的相关理论对地铁工程进行沉降预测，同时建立组合预测模型，结果显示该模型具有很稳定的预测效果；何君等[5]采用GM(1，1)灰色模型对吉林市世纪广场北侧挡水墙进行变形监测，并对精度和可行性进行分析，精确度达到良好以上；李树文等[6]以济南轨道交通R2线济钢新村站基坑监测为例，运用GM(1,1)模型预测变形趋势，结果表明模型稳定性较好。但这些都是针对于灰色理论GM(1，1)模型在建筑物沉降方面的研究，鲜有文献对其在基坑钢筋应力监测方面进行分析，钢筋应力监测对确定混凝土结构的工作水平和预测其耐久性具有重要意义。因此，本文针对北京中国尊基坑工程，利用灰色理论GM(1，1)模型对基坑钢筋应力变化进行预测分析，研究GM(1，1)模型在基坑变形监测中的适用性，为基坑变形研究提供一种快速精准的数据分析方法。

1 灰色系统GM(1,1)模型

1.1 GM(1,1)原理

灰色动态模型是以灰色生成函数概念为基础[7-9]、以微分拟合为核心的建模方法，灰色系统理论认为：所有随机量都是在一定时段上、一定范围内变化的灰色量及灰色过程。对于灰色量的处理，不是去寻求其统计规律或概率分布，而是从杂乱无章的原始数据中找出规律，即对数据通过一定的分析方法进行处理后，使其成为有规律的数据列，再建立动态模型[10]。对于原始数据运用一定的方法进行处理，其目的主要有两个方面：一是为了更好地建立数据模型，提供中间信息；二是通过分析原始数据，将其中的波动性进行减弱处理。

灰色系统建模思想主要是通过将时间序列转化为微分方程[11]，从而建立起抽象系统的发展变化动态模型GM(Grey Model)[12]。GM(h,n)是指微分方程的时间连续函数模型，其中，h代表方程的阶数，n代表变量的个数。即：

(1)

一元一阶灰色模型GM(1,1)的微分方程表示式为：

x(0)(k)+az(1)(k)=b

(2)

式中：a为发展系数；b为灰色作用量[13]。

灰色微分方程x(0)(k)+az(1)(k)=b的最小二乘估计参数应满足:

涓涓溪流汇聚浩瀚，滴滴微水蕴成大海。教师只有不断深掘文本源，拓展练笔场，才能让学生有话想倾诉，有话可表达，才能让学生渐入“我笔书我心”的悠然境界，从而让小练笔这种短、平、快的训练方式真正成为语文课堂中一道亮丽的风景线。

(3)

1.2 GM(1,1)模型精度检验

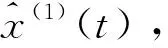
(4)

(5)

(6)

后验差比值计算公式为：

(7)

小误差概率计算公式为：

p={e(t)<0.674 5s1}

(8)

根据后验差比值(c)和小误差概率(p)的值确定模型精度等级，详细评判标准见表1。

表1 各指标的数值与其对应精度Table 1 Numbers of indicators and their corresponding accuracy

若此模型经残差检验、关联度检验和后验差检验都能通过，则可以用所建模型进行预测。否则，需要进行残差修正[16]。

2 灰色系统模型在基坑钢筋应力监测中的应用

2.1 钢筋应力监测数据

北京中国尊基坑工程位于北京市朝阳区国贸桥东北侧，东至金和东路，南邻规划中的绿地，西至金和路，北至光华路，基础埋深约38 m，局部达到40 m，其基础底板东西长136 m，南北宽84 m，塔楼区、过度区基础底板厚度分别为6.5 m、4.5 m，建筑高度约528 m，占地面积11 478 m2，在施工过程中定期对监测点的钢筋应力进行观测。本文从东西管廊监测点处编号为YL-07-01的钢筋应力数据中选取13期数据进行灰色系统分析(表2)，其中前8期数据用于进行灰色系统建模，后5期数据用于模型预测。

表2 钢筋应力监测数据Table 2 Stress monitoring data of reinforcement bars

2.2 模型精度检验

通常由离散点所组成的序列并不可导，不具备像光滑连续函数处处可导的特性，所以不能根据导数对序列的光滑性进行研究。通过对该序列进行光滑性检验，使其与某可导连续函数曲线具有大致相近的特点，因此近似认为该序列是光滑序列[17]。

根据灰色系统理论对原始序列进行1次累加(AGO)后，得到一个新的序列，即：

x(1)(t)=(x(1)(1),x(1)(2),…,x(1)(n))

(9)

对x(0)(t)进行准光滑性检验得：

(10)

当ρ(t)<0.5时， 准光滑条件成立， 且p(t)是光滑比， 对数据进行光滑性检验的结果如表3所示。

表3 光滑性检验Table 3 Smoothness test

从表3可以看出，当期次t>3时，光滑比ρ(t)<0.5，准光滑条件成立。

(2)级比检验

检验x(1)是否具有准指数规律，其中级比序列计算公式为：

(11)

令a=max(σ(1)(t))，b=min(σ(1)(t))，δ=a-b，当δ<0.5时，称x(1)具有指数规律，可以对其进行GM(1,1)模型建模，σ(1)(t)称为序列x(1)的级比[18]。经计算所得级比数值见表 4。

表4 级比序列Table 4 Sequence of stepwise ratio

当级比数值均落在区间(e-2/(n+1)，e2/(n+1))即(0.800 7,1.248 8)内，表明数据序列满足准指数规律，可以进行GM(1,1)模型建模[19]。

(3)模型参数估计

通过构建数据矩阵和矩阵向量，并利用最小二乘法估计模型参数，得a=-0.186 8，u=1.447 7，因此模型表达式为：

X(K+1)=10.160 9*exp(0.186 78K)-7.750 9

(12)

(4)生成数列预测值及拟合效果图

采用所建灰色理论GM(1,1)模型(式12)对基坑钢筋应力变形值进行预测，并对预测精度进行评定，最终生成拟合效果图。从拟合效果图(图1)中可以看出，对于线性的数据使用GM(1，1)模型预测，拟合效果很好，模型对数据的预测结果如表5所示。

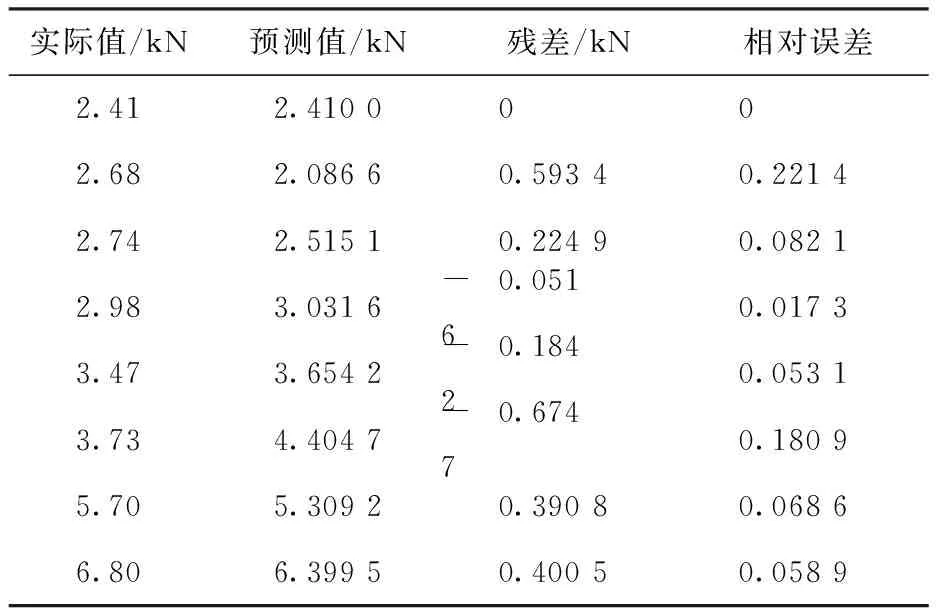
表5 数列预测值及其误差Table 5 Sequence prediction values and their errors

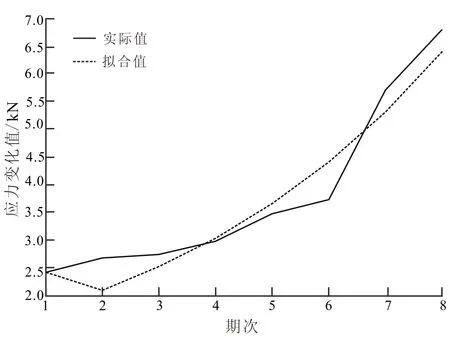
图1 拟合效果图Fig.1 Fitting result diagram

(5)模型检验

利用东西管廊监测点(YL-07-01)的8期监测数据，计算得出GM(1，1)模型的后验差比值c=0.254 5、小误差概率p=1(表6)，根据表1模型精度等级表可以看出，模型适用性较强，精度等级为一级。

表6 模型检验值Table 6 Model test values

(6)预测分析

根据1～8期监测数据建立模型，向后预测5期数据，预测值、观测值和相对误差值如表7所示。结果表明，5期以内的变形预测都具有良好的效果。同时根据预测值和观测值数据生成两者的对比图(图2)。

表7 预测值及其与观测值的相对误差Table 7 Prediction values and its relative errors with observation value

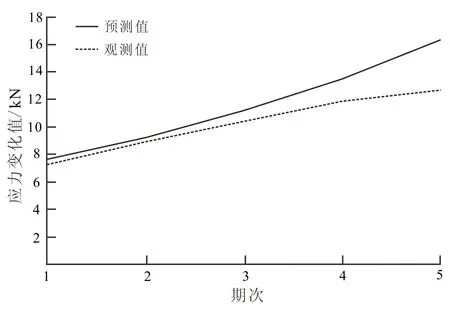
图2 预测值与观测值对比Fig.2 Comparison of predicted and observed values

2.3 结果分析

利用北京中国尊基坑工程中东西管廊监测点(YL-07-01)的8期监测数据，通过后验差检验法求得GM(1,1)模型对应的发展系数，后验差比值c=0.254 5，小误差概率p=1，预测模型的精度等级为一级。同时运用GM(1,1)模型对9～13期数据进行预测，从表7和图2中的数据可以看出，前3期预测结果与实测值的相对误差最大值为0.078 7，且预测曲线与观测值对应的曲线非常接近，表明该模型设计合理准确，后2期预测值的精确度并不是很高，属于可行的预测，精确度随时间变化，时间越长，检测的精确度越低。因此，GM(1,1)模型的短期预测效果较好，3期以内的变形预测值精度较高。

3 结论

(1)GM(1,1)模型是灰色系统理论中核心的一种预测模型，在基坑钢筋应力变形监测中适用性较强。本文采用1～8期监测数据建立预测模型对后5期数据进行预测，模型残差<0.7 kN，预测结果前3期相对误差<0.08，表明该模型对基坑的变形值进行预测可行且可靠，运用该模型可以协助施工人员进行风险控制。

(2)GM(1,1)模型可对基坑变形中一些随机性波动较大、难以拟合的数据进行有序预测，且具有较高精度。同时，通过将后5期监测数据与预测数据进行对比，可以看出该模型适合短期预测，在短期的预测中精准度有保障，时间上采取3周期为好，可为基坑变形监测提供更有价值的参考。